《理論》〈電磁気〉[H28:問1] 三つの導体からなる同心球コンデンサに関する計算問題

1 【問題】
2 【ワンポイント解説】
- 2.1 【関連する「電気の神髄」記事】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，三つの導体からなる同心球コンデンサに関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

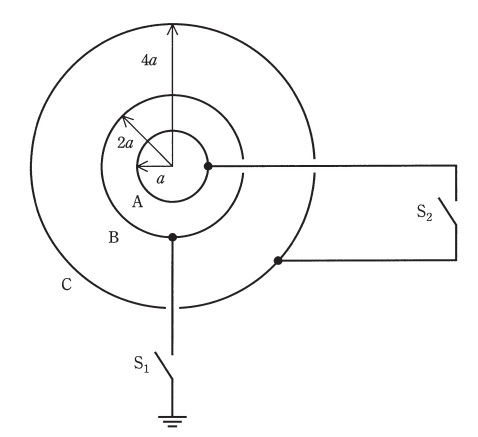
図のように，半径$ \ a \ $，$ \ 2a \ $，$ \ 4a \ $の三つの導体球面$ \ \mathrm {A} \ $，$ \ \mathrm {B} \ $，$ \ \mathrm {C} \ $が同心となるように真空中に置かれている。その厚さは無視できる。導体$ \ \mathrm {B} \ $及び$ \ \mathrm {C} \ $には穴が開けられてそこから導線が引き出されていて，スイッチ$ \ \mathrm {S_{1}} \ $を閉じると導体$ \ \mathrm {B} \ $が接地され，スイッチ$ \ \mathrm {S_{2}} \ $を閉じると導体$ \ \mathrm {A} \ $及び$ \ \mathrm {C} \ $が短絡されるようになっている。
ただし，穴は十分小さく，かつ導線及びスイッチは周りの空間と絶縁されており，その影響は無視できるものとする。また，真空中の誘電率は$ \ \varepsilon _{0} \ $とする。
最初にスイッチ$ \ \mathrm {S_{1}} \ $及び$ \ \mathrm {S_{2}} \ $はともに開いており，導体$ \ \mathrm {A} \ $には電荷$ \ Q \ $が与えられている。このとき，無限遠を接地電位(零)としたときの導体$ \ \mathrm {A} \ $の電位は$ \ \fbox {　（１）　} \ $であり，静電容量は$ \ \fbox {　（２）　} \ $である。また，導体$ \ \mathrm {A} \ $より内側の空間における電界の大きさは$ \ \fbox {　（３）　} \ $である。
次に，スイッチ$ \ \mathrm {S_{1}} \ $を閉じて十分時間が経ったとき，導体$ \ \mathrm {A} \ $の電位は$ \ \fbox {　（４）　} \ $になる。
さらに，スイッチ$ \ \mathrm {S_{1}} \ $を閉じたままスイッチ$ \ \mathrm {S_{2}} \ $を閉じて十分時間が経ったとき，導体$ \ \mathrm {A} \ $に存在する電荷は$ \ \fbox {　（５）　} \ $である。

〔問1の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {Q}{16\pi \varepsilon _{0}a}　　　　　&（ロ）&　\frac {1}{3}Q　　　　　&（ハ）&　4\pi \varepsilon _{0}a \\[ 5pt ] &（ニ）&　0　　　　　&（ホ）&　\frac {3Q}{8\pi \varepsilon _{0}a}　　　　　&（ヘ）&　\frac {1}{5}Q \\[ 5pt ] &（ト）&　\frac {4}{3}\pi \varepsilon _{0}a　　　　　&（チ）&　\frac {Q}{8\pi \varepsilon _{0}a}　　　　　&（リ）&　\frac {Q}{4\pi \varepsilon _{0}a} \\[ 5pt ] &（ヌ）&　\frac {3Q}{4\pi \varepsilon _{0}a}　　　　　&（ル）&　\frac {1}{4}Q　　　　　&（ヲ）&　\frac {16}{3}\pi \varepsilon _{0}a \\[ 5pt ] &（ワ）&　\frac {3Q}{4\pi \varepsilon _{0}a^{2}}　　　　　&（カ）&　\frac {Q}{4\pi \varepsilon _{0}a^{2}}　　　　　&（ヨ）&　\frac {3Q}{16\pi \varepsilon _{0}a}
\end{eqnarray}
\]

【ワンポイント解説】

ガウスの定理と電位の式を用いる問題です。(1)～(4)は二種～三種レベルの問題となります。一種受験者であれば確実に解けるようにしておきたい問題です。

1.ガウスの定理
$ \ Q [ \mathrm {C} ] \ $から出る電気力線は$ \ \displaystyle \frac {Q}{\varepsilon } \ $本であり，電界$ \ E \ $との関係は，任意の閉曲面において，
\[
\int _{S} \boldsymbol E \cdot \mathrm {d}\boldsymbol S = \frac {Q}{\varepsilon }
\] となります。閉局面が球面であれば，
\[
\begin{eqnarray}
4\pi r^{2} E &=& \frac {Q}{\varepsilon } \\[ 5pt ] E &=& \frac {Q}{4\pi \varepsilon r^{2}}
\end{eqnarray}
\] となります。

2.空間上の電位$ \ V \ $
電荷からの距離$ \ r \ $に関する電界$ \ E_{\mathrm {r}} \ $が与えられている時，その場所の電位$ \ V \ $は，無限遠を基準とすると，
\[
V=-\int _{\infty }^{r}E_{\mathrm {r}}\mathrm {d}r
\] で求められます。

【関連する「電気の神髄」記事】

　　同心球コンデンサの静電容量

【解答】

(1)解答：リ
$ \ r＞a \ $における電界$ \ E \ $は，ガウスの定理より，
\[
E = \frac {Q}{4\pi \varepsilon _{0}r^{2}}
\] であるから，導体$ \ \mathrm {A} \ $の電位$ \ V \ $は，
\[
\begin{eqnarray}
V &=& -\int _{\infty }^{a}E \mathrm {d}r \\[ 5pt ] &=& -\int _{\infty }^{a} \frac {Q}{4\pi \varepsilon _{0}r^{2}}\mathrm {d}r \\[ 5pt ] &=& \frac {Q}{4\pi \varepsilon _{0}}\left[ \frac {1}{r}\right] _{\infty }^{a}\\[ 5pt ] &=& \frac {Q}{4\pi \varepsilon _{0}a}
\end{eqnarray}
\] と求められる。

(2)解答：ハ
(1)の解答式より静電容量$ \ C \ $は
\[
\begin{eqnarray}
C &=& \frac {Q}{V} \\[ 5pt ] &=& 4\pi \varepsilon _{0}a
\end{eqnarray}
\] と求められる。

(3)解答：ニ
導体$ \ \mathrm {A} \ $の内側には電荷はなく，電界が現れないので，電界の大きさは$ \ 0 \ $である。

(4)解答：チ
スイッチ$ \ \mathrm {S_{1}} \ $を閉じて十分時間が経つと，導体$ \ \mathrm {B} \ $の電位は零となるので，その時の導体$ \ \mathrm {A} \ $の電位$ \ V_{\mathrm {A}}^{\prime } \ $は，
\[
\begin{eqnarray}
V_{\mathrm {A}}^{\prime } &=& -\int _{2a }^{a}E \mathrm {d}r \\[ 5pt ] &=& -\int _{2a }^{a} \frac {Q}{4\pi \varepsilon _{0}r^{2}}\mathrm {d}r \\[ 5pt ] &=& \frac {Q}{4\pi \varepsilon _{0}}\left[ \frac {1}{r}\right] _{2a}^{a}\\[ 5pt ] &=& \frac {Q}{4\pi \varepsilon _{0}}\left( \frac {1}{a}-\frac {1}{2a}\right) \\[ 5pt ] &=& \frac {Q}{8\pi \varepsilon _{0}a}
\end{eqnarray}
\] と求められる。

(5)解答：ヘ
スイッチ$ \ \mathrm {S_{1}} \ $を閉じたままスイッチ$ \ \mathrm {S_{2}} \ $を閉じて十分時間が経つと，導体$ \ \mathrm {A} \ $と導体$ \ \mathrm {C} \ $の電位が等しくなる。その時，各導体に蓄えらえる電荷を$ \ Q_{\mathrm {A}} \ $，$ \ Q_{\mathrm {B}} \ $，$ \ Q_{\mathrm {C}} \ $とすると，
\[
Q_{\mathrm {A}} +Q_{\mathrm {C}} = Q　　　　　・・・・・・・・①
\] であり，導体$ \ \mathrm {C} \ $の電位$ \ V_{\mathrm {C}} \ $は，
\[
\begin{eqnarray}
V_{\mathrm {C}} &=& -\int _{\infty }^{4a} \frac {Q_{\mathrm {A}} +Q_{\mathrm {B}}+Q_{\mathrm {C}}}{4\pi \varepsilon _{0}r^{2}}\mathrm {d}r \\[ 5pt ] V_{\mathrm {C}} &=& \frac {Q_{\mathrm {A}} +Q_{\mathrm {B}}+Q_{\mathrm {C}}}{16\pi \varepsilon _{0}a} 　・・・・・・・・②
\end{eqnarray}
\] となり，導体$ \ \mathrm {B} \ $の電位$ \ V_{\mathrm {B}} \ $は，
\[
\begin{eqnarray}
V_{\mathrm {B}} &=& -\int _{4a }^{2a} \frac {Q_{\mathrm {A}} +Q_{\mathrm {B}}}{4\pi \varepsilon _{0}r^{2}}\mathrm {d}r +V_{\mathrm {C}} \\[ 5pt ] &=& \frac {Q_{\mathrm {A}} +Q_{\mathrm {B}}}{16\pi \varepsilon _{0}a}+\frac {Q_{\mathrm {A}} +Q_{\mathrm {B}}+Q_{\mathrm {C}}}{16\pi \varepsilon _{0}a} \\[ 5pt ] &=& \frac {2Q_{\mathrm {A}} +2Q_{\mathrm {B}}+Q_{\mathrm {C}}}{16\pi \varepsilon _{0}a}
\end{eqnarray}
\] となる。$ \ V_{\mathrm {B}}=0 \ $であるから，
\[
\begin{eqnarray}
V_{\mathrm {B}} &=& 0 \\[ 5pt ] \frac {2Q_{\mathrm {A}} +2Q_{\mathrm {B}}+Q_{\mathrm {C}}}{16\pi \varepsilon _{0}a} &=& 0 \\[ 5pt ] 2Q_{\mathrm {A}} +2Q_{\mathrm {B}}+Q_{\mathrm {C}}&=& 0 　・・・・・・・・③
\end{eqnarray}
\] となる。導体$ \ \mathrm {A} \ $の電位$ \ V_{\mathrm {A}} \ $は，
\[
\begin{eqnarray}
V_{\mathrm {A}} &=& -\int _{2a }^{a} \frac {Q_{\mathrm {A}}}{4\pi \varepsilon _{0}r^{2}}\mathrm {d}r \\[ 5pt ] &=& \frac {Q_{\mathrm {A}}}{8\pi \varepsilon _{0}a} 　　　　　　・・・・・・・・④
\end{eqnarray}
\] となる。$ \ V_{\mathrm {A}}=V_{\mathrm {C}} \ $であるから，②，④より，
\[
\begin{eqnarray}
V_{\mathrm {A}} &=& V_{\mathrm {C}} \\[ 5pt ] \frac {Q_{\mathrm {A}}}{8\pi \varepsilon _{0}a} &=& \frac {Q_{\mathrm {A}} +Q_{\mathrm {B}}+Q_{\mathrm {C}}}{16\pi \varepsilon _{0}a} \\[ 5pt ] -Q_{\mathrm {A}} +Q_{\mathrm {B}}+Q_{\mathrm {C}}&=& 0 　　・・・・・・・・⑤
\end{eqnarray}
\] となる。①，③，⑤の連立方程式を解くと，
\[
\begin{eqnarray}
Q_{\mathrm {A}} &=& \frac {1}{5}Q \\[ 5pt ] Q_{\mathrm {B}} &=& -\frac {3}{5}Q \\[ 5pt ] Q_{\mathrm {C}} &=& \frac {4}{5}Q
\end{eqnarray}
\] と求められる。