《理論》〈電子理論〉[H29:問7] トランジスタを用いた回路に関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，トランジスタを用いた回路に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

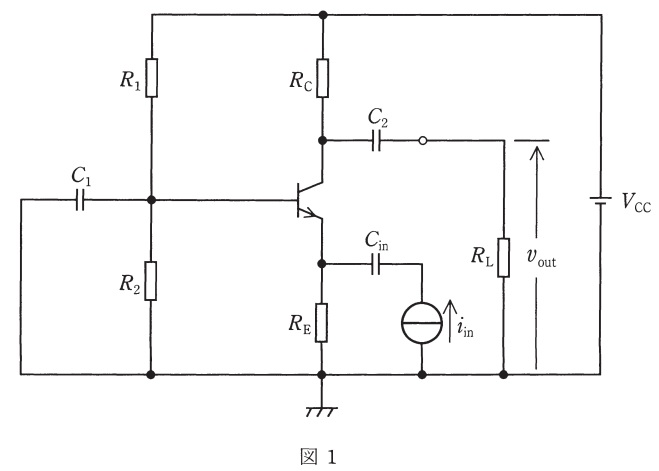
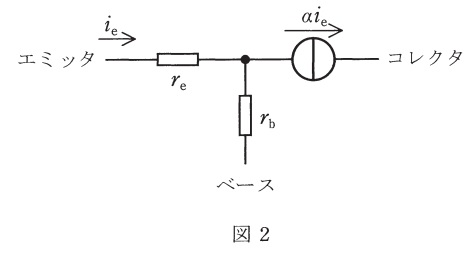
図1の回路において全てのコンデンサは信号周波数で短絡とみなせ，トランジスタの交流等価回路は図2で表されるものとする。
まず，図1の回路の入力電流$ \ i_{\mathrm {in}} \ $を零とし、各節点の電位を求める。$ \ R_{1} \ $を流れる電流よりベース電流が十分小さいとみなせる場合，ベースの電位$ \ V_{\mathrm {B}} \ $は$ \ \fbox {　（１）　} \ $となる。また，このときのコレクタ電流を$ \ I_{\mathrm {C0}} \ $とするとコレクタ電位$ \ V_{\mathrm {C}} \ $は$ \ \fbox {　（２）　} \ $となる。通常，トランジスタは活性領域(順能動領域)で用いられるため，各素子値は$ \ V_{\mathrm {C}} \ $と$ \ V_{\mathrm {B}} \ $とエミッタ電位$ \ V_{\mathrm {E}} \ $が$ \ \fbox {　（３）　} \ $となるように選ばれる。
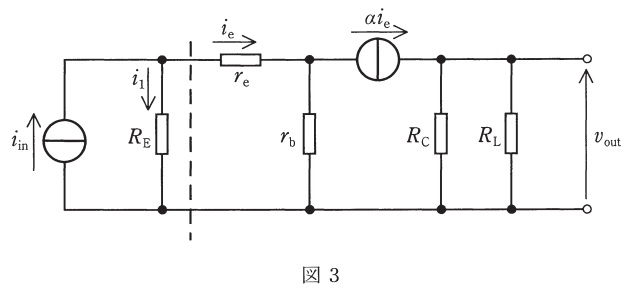
次に，図2を用いて図1の小信号等価回路を描くと図3が得られる。図3において入力電流$ \ i_{\mathrm {in}} \ $は$ \ i_{\mathrm {1}} \ $と$ \ i_{\mathrm {e}} \ $に分流するが，図3中の破線から右側の回路の入力インピーダンスが$ \ \fbox {　（４）　} \ $となることを考慮すると$ \ i_{\mathrm {e}} \ $を求めることができる。出力電圧$ \ v_{\mathrm {out}} \ $は，$ \ R_{\mathrm {C}} \ $と$ \ R_{\mathrm {L}} \ $の並列抵抗に$ \ \alpha i_{\mathrm {e}} \ $が流れることにより生じるため，出力電圧$ \ v_{\mathrm {out}} \ $は$ \ \fbox {　（５）　} \ $と求められる。

〔問7の解答群〕
\[
\begin{eqnarray}
&（イ）&　R_{\mathrm {C}}I_{\mathrm {C0}}　　　&（ロ）&　r_{\mathrm {e}}+( 1-\alpha )r_{\mathrm {b}}　　　&（ハ）&　\frac {\alpha R_{\mathrm {E}}}{r_{\mathrm {e}}+R_{\mathrm {E}}+(1-\alpha )r_{\mathrm {b}}}\frac {R_{\mathrm {C}}R_{\mathrm {L}}}{R_{\mathrm {C}}+R_{\mathrm {L}}}i_{\mathrm {in}} \\[ 5pt ] &（ニ）&　\frac {R_{2}}{R_{1}+R_{2}}V_{\mathrm {CC}}　　　&（ホ）&　R_{\mathrm {E}}I_{\mathrm {C0}}　　　&（ヘ）&　V_{\mathrm {C}} \gt V_{\mathrm {B}}かつV_{\mathrm {B}} \gt V_{\mathrm {E}} \\[ 5pt ] &（ト）&　V_{\mathrm {B}} \gt V_{\mathrm {C}}かつV_{\mathrm {B}} \gt V_{\mathrm {E}}　　　&（チ）&　r_{\mathrm {e}}　　　&（リ）&　\frac {\alpha R_{\mathrm {E}}}{r_{\mathrm {e}}+r_{\mathrm {b}}+R_{\mathrm {E}}}\frac {R_{\mathrm {C}}R_{\mathrm {L}}}{R_{\mathrm {C}}+R_{\mathrm {L}}}i_{\mathrm {in}} \\[ 5pt ] &（ヌ）&　V_{\mathrm {C}} \gt V_{\mathrm {B}}かつV_{\mathrm {E}} \gt V_{\mathrm {B}}　　　　&（ル）&　r_{\mathrm {e}}+r_{\mathrm {b}}　　　&（ヲ）&　\frac {-\alpha R_{\mathrm {E}}}{r_{\mathrm {e}}+R_{\mathrm {E}}+(1-\alpha )r_{\mathrm {b}}}\frac {R_{\mathrm {C}}R_{\mathrm {L}}}{R_{\mathrm {C}}+R_{\mathrm {L}}}i_{\mathrm {in}} \\[ 5pt ] &（ワ）&　\frac {R_{1}}{R_{1}+R_{2}}V_{\mathrm {CC}}　　　&（カ）&　\frac {R_{1}R_{2}}{R_{1}+R_{2}}i_{\mathrm {in}}　　　&（ヨ）&　V_{\mathrm {CC}}-R_{\mathrm {C}}I_{\mathrm {C0}}
\end{eqnarray}
\]

【ワンポイント解説】

問7は毎年電子回路が出題されています。オペアンプが最も多いですが，バイポーラトランジスタの問題も出題されます。配点が高く問題がパターン化されていることが多いので，問題慣れすれば，得点源となる可能性が高いです。

【解答】

(1)解答：ニ
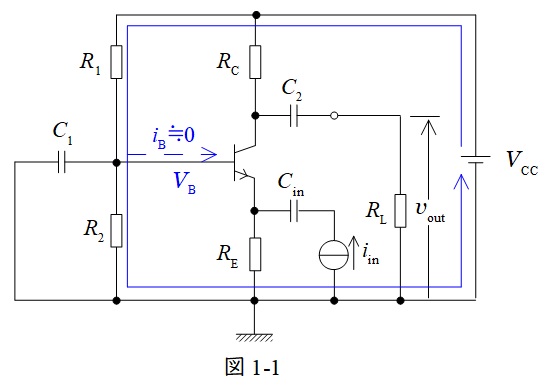
図1-1に示すようにベース電位$ \ V_{\mathrm {B}} \ $を求めるには，青色部の閉回路を用いて求めればよい。ベース電流$ \ i_{\mathrm {B}}≒ 0 \ $であり，$ \ V_{\mathrm {B}} \ $は$ \ R_{1} \ $と$ \ R_{2} \ $の分圧であるから，
\[
\begin{eqnarray}
V_{\mathrm {B}}&=&\frac {R_{2}}{R_{1}+R_{2}}V_{\mathrm {CC}} \\[ 5pt ] \end{eqnarray}
\] となる。

(2)解答：ヨ
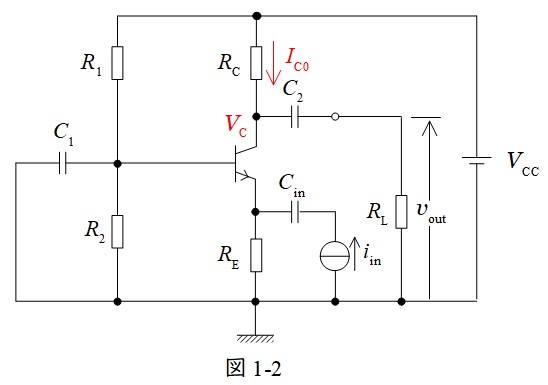
図1-2に示すように，コレクタ電位$ \ V_{\mathrm {C}} \ $は$ \ V_{\mathrm {CC}} \ $から$ \ R_{\mathrm {C}} \ $の電圧降下分を差し引けば良いので，
\[
\begin{eqnarray}
V_{\mathrm {C}}&=&V_{\mathrm {CC}}-R_{\mathrm {C}}I_{\mathrm {C0}} \\[ 5pt ] \end{eqnarray}
\] となる。

(3)解答：ヘ
トランジスタを活性領域で用いるには，ベース電流がベース→エミッタ，コレクタ電流がコレクタ→エミッタに流れる必要がある。よって，トランジスタに順方向電圧がかかるようにするには，$ \ V_{\mathrm {C}} \gt V_{\mathrm {B}} \gt V_{\mathrm {E}} \ $とならなければならない。

(4)解答：ロ
図3の回路において，$ \ r_{\mathrm {b}} \ $に流れる電流$ \ i_{\mathrm {b}} \ $は，
\[
\begin{eqnarray}
i_{\mathrm {b}}&=&i_{\mathrm {e}}-\alpha i_{\mathrm {e}}=(1-\alpha ) i_{\mathrm {e}} \\[ 5pt ] \end{eqnarray}
\] となる。図の電流源から右側の抵抗を$ \ r_{\mathrm {c}} \ $とすると，
\[
\begin{eqnarray}
r_{\mathrm {c}}\alpha i_{\mathrm {e}} &=& r_{\mathrm {b}}(1-\alpha ) i_{\mathrm {e}} \\[ 5pt ] r_{\mathrm {c}} &=& \frac {1-\alpha}{\alpha}r_{\mathrm {b}} \\[ 5pt ] \end{eqnarray}
\] となるから，入力インピーダンス$ \ R_{\mathrm {in}} \ $は，
\[
\begin{eqnarray}
R_{\mathrm {in}} &=& r_{\mathrm {e}}+\frac {r_{\mathrm {b}}r_{\mathrm {c}}}{r_{\mathrm {b}}+r_{\mathrm {c}}} \\[ 5pt ] &=& r_{\mathrm {e}}+\frac {r_{\mathrm {b}}\cdot \frac {1-\alpha}{\alpha}r_{\mathrm {b}}}{r_{\mathrm {b}}+\frac {1-\alpha}{\alpha}r_{\mathrm {b}}} \\[ 5pt ] &=& r_{\mathrm {e}}+(1-\alpha ) r_{\mathrm {b}}
\end{eqnarray}
\] と求められる。

(5)解答：ハ
エミッタ電流$ \ i_{\mathrm {e}} \ $は$ \ i_{\mathrm {in}} \ $，$ \ R_{\mathrm {E}} \ $，$ \ R_{\mathrm {in}} \ $を用いて，
\[
\begin{eqnarray}
i_{\mathrm {e}} &=& \frac {R_{\mathrm {E}}}{R_{\mathrm {E}}+R_{\mathrm {in}}}i_{\mathrm {in}} \\[ 5pt ] &=& \frac {R_{\mathrm {E}}}{R_{\mathrm {E}}+r_{\mathrm {e}}+(1-\alpha ) r_{\mathrm {b}}}i_{\mathrm {in}}　・・・・・・　① \\[ 5pt ] \end{eqnarray}
\] となる。また，$ \ v_{\mathrm {out}} \ $は$ \ R_{\mathrm {C}} \ $と$ \ R_{\mathrm {L}} \ $の電圧降下なので，
\[
\begin{eqnarray}
v_{\mathrm {out}}&=&\frac {R_{\mathrm {C}}R_{\mathrm {L}}}{R_{\mathrm {C}}+R_{\mathrm {L}}}\alpha i_{\mathrm {e}} \\[ 5pt ] \end{eqnarray}
\] となる。よって，①を代入すると，
\[
\begin{eqnarray}
v_{\mathrm {out}} &=& \frac {R_{\mathrm {C}}R_{\mathrm {L}}}{R_{\mathrm {C}}+R_{\mathrm {L}}}\alpha i_{\mathrm {e}} \\[ 5pt ] &=& \frac {R_{\mathrm {C}}R_{\mathrm {L}}}{R_{\mathrm {C}}+R_{\mathrm {L}}}\alpha \frac {R_{\mathrm {E}}}{R_{\mathrm {E}}+r_{\mathrm {e}}+(1-\alpha ) r_{\mathrm {b}}}i_{\mathrm {in}} \\[ 5pt ] &=& \frac {\alpha R_{\mathrm {E}}}{r_{\mathrm {e}}+R_{\mathrm {E}}+(1-\alpha )r_{\mathrm {b}}}\frac {R_{\mathrm {C}}R_{\mathrm {L}}}{R_{\mathrm {C}}+R_{\mathrm {L}}}i_{\mathrm {in}} \\[ 5pt ] \end{eqnarray}
\] と求められる。