【問題】
【難易度】★★☆☆☆(やや易しい)
次の文章は,磁界によって生じる力に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。なお,\( \ \mu _{0} \ \)は真空の透磁率である。
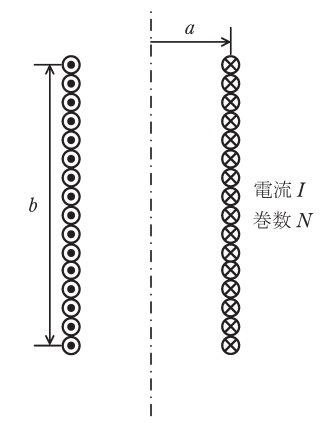
図に示すような半径\( \ a \ \),長さ\( \ b \ \),巻数\( \ N \ \)の空心ソレノイドを考える。ただし,\( \ a≪b \ \)であり,ソレノイドには一定の電流\( \ I \ \)が流れている。ソレノイドの内部には軸方向の磁束密度が一様に形成されており,ソレノイドの外部では磁束密度は零と仮定する。ソレノイド内部の磁束密度の大きさ\( \ B \ \)は,
\[
\begin{eqnarray}
B&=& \ \fbox { (1) } \ \\[ 5pt ]
\end{eqnarray}
\]
と表されるので,ソレノイドのインダクタンスは\( \ L= \ \fbox { (2) } \ \)となる。
仮想変位の原理を用いて,ソレノイドを流れる電流に働く磁界の力を求める。ソレノイド内部に蓄積された磁界のエネルギーは\( \ W= \ \fbox { (3) } \ \)となるので,ソレノイドの軸方向に働く力\( \ F \ \)は,電流一定の条件下で磁界のエネルギーを長さ\( \ b \ \)で偏微分することで求められる。この力は磁束密度\( \ B \ \)を用いて,
\[
\begin{eqnarray}
F&=& \frac{ \partial W }{ \partial b } = \frac {B^{2}}{2\mu _{0}}\times \fbox { (4) } \\[ 5pt ]
\end{eqnarray}
\]
と表され,ソレノイドの\( \ \fbox { (5) } \ \)方向に働く。\( \ \displaystyle \frac {B^{2}}{2\mu _{0}} \ \)は単位面積あたりに働くマクスウェルの応力とよばれる。
〔問2の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {\mu _{0}\pi a^{2}N}{b} &(ロ)& \frac {\mu _{0}NI}{2b} &(ハ)& \frac {\mu _{0}NI}{b} \\[ 5pt ]
&(ニ)& \frac {\mu _{0}\pi a^{2}N^{2}I^{2}}{2b^{2}} &(ホ)& \frac {\mu _{0}\pi a^{2}NI^{2}}{2b} &(ヘ)& \frac {\mu _{0}\pi a^{2}N^{2}I^{2}}{2b} \\[ 5pt ]
&(ト)& 2\pi ab &(チ)& 径を拡げる &(リ)& 長さを伸ばす \\[ 5pt ]
&(ヌ)& \frac {2\mu _{0}NI}{b} &(ル)& \frac {\mu _{0}\pi a^{2}N^{2}}{b} &(ヲ)& \pi a^{2} \\[ 5pt ]
&(ワ)& 長さを縮める &(カ)& -\pi a^{2} &(ヨ)& \frac {\mu _{0}\pi a^{2}N^{2}}{b^{2}} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
ソレノイド内部の磁界に関する問題です。電磁気の内容を総合的に理解しているか問うような問題となっています。
1.ソレノイドの内部の磁界\( \ H \ \)
巻数\( \ N \ \),電流\( \ I \ \),長さ\( \ l \ \)のソレノイドの内部鉄心の磁界の強さ\( \ H \ \)は,アンペアの周回積分の法則により,
\[
\begin{eqnarray}
\Sigma I &=& \int _{\mathrm {c}} \boldsymbol H \cdot \mathrm {d}\boldsymbol l \\[ 5pt ]
NI &=& Hl \\[ 5pt ]
H &=& \frac {NI}{l} \\[ 5pt ]
\end{eqnarray}
\]
と求められます。
2.ソレノイドの内部の磁束\( \ \mathit {\Phi } \ \)
ソレノイド内部の透磁率が\( \ \mu \ \),磁界の強さが\( \ H \ \)であるとき,内部の磁束密度\( \ B \ \)は,
\[
\begin{eqnarray}
B &=& \mu H \\[ 5pt ]
\end{eqnarray}
\]
となります。ソレノイドの内部の磁束\( \ \mathit {\Phi } \ \)は内部の磁束密度が一様であるとして,内部の断面積を\( \ S \ \)とすると,
\[
\begin{eqnarray}
\mathit {\Phi } &=& BS \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.自己インダクタンス\( \ L \ \)
問題図のようなソレノイドにおいて,巻数\( \ N \ \)のコイルに電流\( \ I \ \)を流した時の鉄心の磁束\( \ \phi \ \)と比例定数\( \ L \ \)の関係は,起電力\( \ e \ \)を求める関係より,
\[
\begin{eqnarray}
-N\frac {\Delta \phi }{\Delta t}&=&-L\frac {\Delta I}{\Delta t} \\[ 5pt ]
N\phi &=&LI \\[ 5pt ]
L &=&\frac {N\phi }{I} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ L \ \)を自己インダクタンスと言います。
【関連する「電気の神髄」記事】
【解答】
(1)解答:ハ
ソレノイドの外部の磁束密度を零と仮定するので,ワンポイント解説「1.ソレノイドの内部の磁界\( \ H \ \)」の通り,ソレノイド内部の磁界の強さ\( \ H \ \)は,
\[
\begin{eqnarray}
NI &=& Hb \\[ 5pt ]
H &=& \frac {NI}{b} \\[ 5pt ]
\end{eqnarray}
\]
であるので,ワンポイント解説「2.ソレノイドの内部の磁束\( \ \mathit {\Phi } \ \)」の通り,ソレノイド内部の磁束密度\( \ B \ \)は,
\[
\begin{eqnarray}
B &=& \mu_{0} H \\[ 5pt ]
&=& \frac {\mu_{0}NI}{b} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ル
ワンポイント解説「2.ソレノイドの内部の磁束\( \ \mathit {\Phi } \ \)」の通り,ソレノイド内部の磁束\( \ \mathit {\Phi } \ \)は,
\[
\begin{eqnarray}
\mathit {\Phi } &=& BS \\[ 5pt ]
&=& \frac {\mu_{0}NI}{b}\cdot \pi a^{2} \\[ 5pt ]
&=& \frac {\mu_{0}\pi a^{2}NI}{b} \\[ 5pt ]
\end{eqnarray}
\]
となり,ワンポイント解説「3.自己インダクタンス\( \ L \ \)」の通り,自己インダクタンス\( \ L \ \)は,
\[
\begin{eqnarray}
N\phi &=&LI \\[ 5pt ]
L &=&\frac {N\phi }{I} \\[ 5pt ]
&=&\frac {N}{I}\cdot \frac {\mu_{0}\pi a^{2}NI}{b} \\[ 5pt ]
&=&\frac {\mu _{0}\pi a^{2}N^{2}}{b} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ヘ
ソレノイドに蓄えられる磁界のエネルギー\( \ W \ \)は,
\[
\begin{eqnarray}
W &=&\frac {1}{2}LI^{2} \\[ 5pt ]
&=&\frac {1}{2}\cdot \frac {\mu _{0}\pi a^{2}N^{2}}{b}\cdot I^{2} \\[ 5pt ]
&=&\frac {\mu _{0}\pi a^{2}N^{2}I^{2}}{2b} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:カ
題意より,
\[
\begin{eqnarray}
F&=& \frac{ \partial W }{ \partial b } \\[ 5pt ]
&=& \frac{ \partial }{ \partial b }\left[ \frac {\mu _{0}\pi a^{2}N^{2}I^{2}}{2b}\right] \\[ 5pt ]
&=& \frac {\mu _{0}\pi a^{2}N^{2}I^{2}}{2}\frac{ \partial }{ \partial b }\left[ \frac {1}{b}\right] \\[ 5pt ]
&=& \frac {\mu _{0}\pi a^{2}N^{2}I^{2}}{2}\left( -\frac {1}{b^{2}}\right) \\[ 5pt ]
&=& -\frac {\mu _{0}\pi a^{2}N^{2}I^{2}}{2b^{2}} \\[ 5pt ]
&=& \frac {B^{2}}{2\mu _{0}}\times \left( -\pi a^{2}\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ワ
(4)の解答式より,力は負の方向に働くので,ソレノイドの長さを縮める方向に働きます。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん