【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,円板状の電荷分布が作り出す電界に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。なお,電位は無限遠点を基準とする。
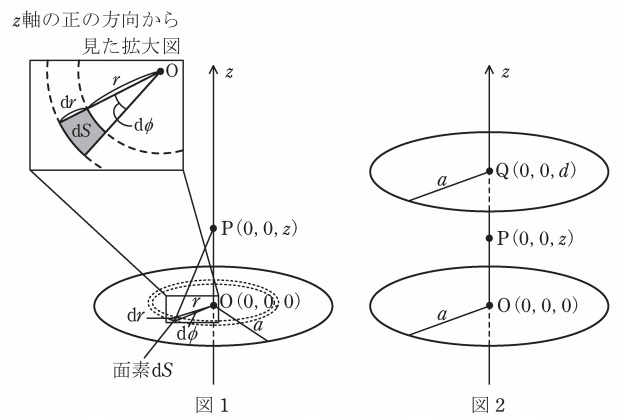
図1のように電荷が一様な面密度\( \ \sigma \ \)(ただし\( \ \sigma >0 \ \)とする)で分布した半径\( \ a \ \)の薄い円板が真空中(誘電率\( \ \varepsilon _{0} \ \))に存在している。円板の厚みはその半径に比べて十分に薄いものとし,円板の軸を\( \ z \ \)軸とした円筒座標\( \ \left( r, \phi ,z \right) \ \)を定め,円板の中心を原点\( \ \mathrm {O} \left( 0, 0 ,0 \right) \ \)とする。
円板上の半径\( \ r \ \)の位置における微小半径\( \ \mathrm {d}r \ \),微小角度\( \ \mathrm {d}\phi \ \)の領域(面素)の面積は\( \ \mathrm {d}S=r\mathrm {d}r\mathrm {d}\phi \ \)と表されるので,この領域に含まれる電荷が\( \ z \ \)軸上の点\( \ \mathrm {P} \left( 0, 0 ,z \right) \ \)(ただし\( \ z >0 \ \)とする)に作る電位は,
\[
\begin{eqnarray}
\mathrm {d}V&=&\frac {\mathrm {d}r\mathrm {d}\phi}{4\pi \varepsilon _{0}}\times \ \fbox { (1) } \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,円板上の電荷全体が点\( \ \mathrm {P} \ \)に作る電位は,
\[
\begin{eqnarray}
V&=&\frac {1}{4\pi \varepsilon _{0}}\times \int _{0}^{2\pi }\int _{0}^{a} \ \fbox { (1) } \ \mathrm {d}r\mathrm {d}\phi \\[ 5pt ]
&=& \ \fbox { (2) } \\[ 5pt ]
\end{eqnarray}
\]
となる。なお,必要であれば,
\[
\begin{eqnarray}
\frac {\mathrm {d}}{\mathrm {d}x}\sqrt {x^{2}+1}&=&\frac {x}{\sqrt {x^{2}+1}} \\[ 5pt ]
\end{eqnarray}
\]
という関係式を用いてもよい。
\( \ \fbox { (2) } \ \)の結果を用いると,このとき点\( \ \mathrm {P} \ \)に形成される\( \ z \ \)方向電界は,
\[
\begin{eqnarray}
E_{\mathrm {z1}}&=&-\frac {\mathrm {d}V}{\mathrm {d}z}= \ \fbox { (3) } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
次に,図2に示すように点\( \ \mathrm {Q} \left( 0, 0 ,d \right) \ \)(ただし\( \ d >0 \ \)とする)を中心とした半径\( \ a \ \)の十分に薄い円板上にも一様な面密度\( \ -\sigma \ \)で電荷が分布している場合を考える。点\( \ \mathrm {P} \ \)が点\( \ \mathrm {O} \ \)と点\( \ \mathrm {Q} \ \)の間にあるとすると,点\( \ \mathrm {P} \ \)の\( \ z \ \)方向電界は重ね合わせにより,
\[
\begin{eqnarray}
E_{\mathrm {z2}}&=& \ \fbox { (4) } \\[ 5pt ]
\end{eqnarray}
\]
となる。二つの円板の半径\( \ a \ \)が円板間距離\( \ d \ \)に対して十分大きい場合には,円板間の電界は一様であるとみなせ,その大きさは\( \ \fbox { (5) } \ \)となる。
〔問1の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {\sigma }{\varepsilon _{0}} &(ロ)& \frac {\sigma }{2\varepsilon _{0}}\frac {z^{2}}{z^{2}+a^{2}} &(ハ)& \frac {\sigma }{2\varepsilon _{0}}\left[ 2-\frac {z}{\sqrt {z^{2}+a^{2}}}-\frac {d-z}{\sqrt {\left( d-z\right) ^{2}+a^{2}}} \right] \\[ 5pt ]
&(ニ)& \frac {\sigma r}{z^{2}+r^{2}} &(ホ)& \frac {\sigma }{2\varepsilon _{0}}\frac {a^{2}}{z^{2}+a^{2}} &(ヘ)& \frac {\sigma }{2\varepsilon _{0}}\left( \sqrt {z^{2}+a^{2}}-z \right) \\[ 5pt ]
&(ト)& \frac {\sigma r}{\sqrt {z^{2}+r^{2}}} &(チ)& \frac {\sigma }{2\varepsilon _{0}} &(リ)& \frac {\sigma }{2\varepsilon _{0}}\left[ \frac {z^{2}}{z^{2}+a^{2}}-\frac {\left( d-z\right) ^{2}}{\left( d-z\right) ^{2}+a^{2}} \right] \\[ 5pt ]
&(ヌ)& \frac {\sigma }{2\varepsilon _{0}}z &(ル)& \frac {\sigma r}{\left( z^{2}+r^{2}\right) ^{\frac {3}{2}}} &(ヲ)& \frac {\sigma }{2\varepsilon _{0}}\left[ \frac {a^{2}}{z^{2}+a^{2}}-\frac {a^{2}}{\left( d-z\right) ^{2}+a^{2}} \right] \\[ 5pt ]
&(ワ)& 0 &(カ)& \frac {\sigma }{2\varepsilon _{0}}a &(ヨ)& \frac {\sigma }{2\varepsilon _{0}}\left( 1-\frac {z}{\sqrt {z^{2}+a^{2}}} \right) \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
円板が作る電位,電界に関する問題です。
(2)や(3)の微分積分の計算が一番の肝となる問題です。難易度は高めとしていますが,易しいと感じる受験生,難しいと感じる受験生が大きく分かれる問題であり,微分積分の計算に慣れている方であれば完答も十分に目指せると思います。
1.点電荷が作る電界の強さ\( \ E \ \)
真空中(誘電率\( \ \varepsilon _{0} \ \))で点電荷\( \ Q \ \)が作る電界の大きさ\( \ E \ \)は,距離\( \ r \ \)の地点で,
\[
\begin{eqnarray}
E&=&\frac {Q}{4\pi \varepsilon _{0}r^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.点電荷が作る電位\( \ V \ \)
真空中(誘電率\( \ \varepsilon _{0} \ \))で点電荷\( \ Q \ \)が距離\( \ r \ \)の地点に作る電位\( \ V \ \)は,
\[
\begin{eqnarray}
V&=&\frac {Q}{4\pi \varepsilon _{0}r} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)解答:ト
図1の微小面積\( \ \mathrm {d}S \ \)における電荷量\( \ \mathrm {d}Q \ \)は,
\[
\begin{eqnarray}
\mathrm {d}Q&=&\sigma \mathrm {d}S \\[ 5pt ]
&=&\sigma r\mathrm {d}r\mathrm {d}\phi \\[ 5pt ]
\end{eqnarray}
\]
であり,\( \ \mathrm {d}Q \ \)から点\( \ \mathrm {P} \ \)までの距離\( \ l \ \)は,
\[
\begin{eqnarray}
l&=&\sqrt {r^{2}+z^{2}} \\[ 5pt ]
\end{eqnarray}
\]
であるから,ワンポイント解説「2.点電荷が作る電位\( \ V \ \)」の通り\( \ \mathrm {d}Q \ \)が点\( \ \mathrm {P} \left( 0, 0 ,z \right) \ \)に作る電位\( \ \mathrm {d}V \ \)は,
\[
\begin{eqnarray}
\mathrm {d}V&=&\frac {\mathrm {d}Q}{4\pi \varepsilon _{0}l} \\[ 5pt ]
&=&\frac {\sigma r\mathrm {d}r\mathrm {d}\phi }{4\pi \varepsilon _{0}\sqrt {r^{2}+z^{2}}} \\[ 5pt ]
&=&\frac {\mathrm {d}r\mathrm {d}\phi}{4\pi \varepsilon _{0}}\times \frac {\sigma r}{\sqrt {z^{2}+r^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ヘ
\[
\begin{eqnarray}
V&=&\frac {1}{4\pi \varepsilon _{0}}\times \int _{0}^{2\pi }\int _{0}^{a} \frac {\sigma r}{\sqrt {z^{2}+r^{2}}} \mathrm {d}r\mathrm {d}\phi \\[ 5pt ]
&=&\frac {\sigma }{4\pi \varepsilon _{0}}\times \int _{0}^{2\pi }\int _{0}^{a} \frac {\displaystyle \frac {r}{z}}{\displaystyle \sqrt {\left( \frac {r}{z}\right) ^{2}+1}} \mathrm {d}r\mathrm {d}\phi \\[ 5pt ]
\end{eqnarray}
\]
において,\( \ \displaystyle x=\frac {r}{z} \ \)とすると,\( \ \displaystyle \frac {\mathrm {d}x}{\mathrm {d}r}=\frac {1}{z} \ \)すなわち\( \ \displaystyle \mathrm {d}r=z\mathrm {d}x \ \)となり,\( \ r \ \)が\( \ 0 \ \)から\( \ a \ \)まで変化するとき\( \ x \ \)が\( \ 0 \ \)から\( \ \displaystyle \frac {a}{z} \ \)まで変化するので,
\[
\begin{eqnarray}
V&=&\frac {\sigma }{4\pi \varepsilon _{0}}\times \int _{0}^{2\pi }\int _{0}^{a} \frac {\displaystyle \frac {r}{z}}{\displaystyle \sqrt {\left( \frac {r}{z}\right) ^{2}+1}} \mathrm {d}r\mathrm {d}\phi \\[ 5pt ]
&=&\frac {\sigma }{4\pi \varepsilon _{0}}\times \int _{0}^{2\pi }\int _{0}^{\frac {a}{z}} \frac {x}{\displaystyle \sqrt {x ^{2}+1}} z\mathrm {d}x\mathrm {d}\phi \\[ 5pt ]
&=&\frac {\sigma }{4\pi \varepsilon _{0}}\times \int _{0}^{2\pi }z\int _{0}^{\frac {a}{z}} \frac {x}{\displaystyle \sqrt {x ^{2}+1}} \mathrm {d}x\mathrm {d}\phi \\[ 5pt ]
\end{eqnarray}
\]
と変形できる。ここで,
\[
\begin{eqnarray}
\frac {\mathrm {d}}{\mathrm {d}x}\sqrt {x^{2}+1}&=&\frac {x}{\sqrt {x^{2}+1}} \\[ 5pt ]
\end{eqnarray}
\]
という関係式を用いて計算をすると,
\[
\begin{eqnarray}
V&=&\frac {\sigma }{4\pi \varepsilon _{0}}\times \int _{0}^{2\pi }z\int _{0}^{\frac {a}{z}} \frac {x}{\displaystyle \sqrt {x ^{2}+1}} \mathrm {d}x\mathrm {d}\phi \\[ 5pt ]
&=&\frac {\sigma }{4\pi \varepsilon _{0}}\times \int _{0}^{2\pi }z\left[ \sqrt {x^{2}+1} \right] _{0}^{\frac {a}{z}}\mathrm {d}\phi \\[ 5pt ]
&=&\frac {\sigma }{4\pi \varepsilon _{0}}\times \int _{0}^{2\pi }z\left\{ \sqrt { \left( \frac {a}{z}\right) ^{2}+1 } -\sqrt { \left( 0+1\right) } \right\} \mathrm {d}\phi \\[ 5pt ]
&=&\frac {\sigma }{4\pi \varepsilon _{0}}\times \int _{0}^{2\pi }\left( \sqrt {a ^{2}+z ^{2} } -z \right) \mathrm {d}\phi \\[ 5pt ]
&=&\frac {\sigma }{4\pi \varepsilon _{0}}\left( \sqrt {a ^{2}+z ^{2} } -z \right) \times \int _{0}^{2\pi }\mathrm {d}\phi \\[ 5pt ]
&=&\frac {\sigma }{4\pi \varepsilon _{0}}\left( \sqrt {a ^{2}+z ^{2} } -z \right) \times \left[ \phi \right] _{0}^{2\pi } \\[ 5pt ]
&=&\frac {\sigma }{4\pi \varepsilon _{0}}\left( \sqrt {a ^{2}+z ^{2} } -z \right) \times 2\pi \\[ 5pt ]
&=&\frac {\sigma }{2\varepsilon _{0}}\left( \sqrt {a^{2}+z^{2}}-z \right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ヨ
題意に沿って計算すると,
\[
\begin{eqnarray}
E_{\mathrm {z1}}&=&-\frac {\mathrm {d}V}{\mathrm {d}z} \\[ 5pt ]
&=&-\frac {\mathrm {d}}{\mathrm {d}z}\left\{ \frac {\sigma }{2\varepsilon _{0}}\left( \sqrt {z^{2}+a^{2}}-z \right) \right\} \\[ 5pt ]
&=&-\frac {\sigma }{2\varepsilon _{0}}\frac {\mathrm {d}}{\mathrm {d}z}\left\{ \left( z^{2}+a^{2}\right) ^{\frac {1}{2}}-z \right\} \\[ 5pt ]
&=&-\frac {\sigma }{2\varepsilon _{0}}\left\{ \frac {1}{2}\times 2z\times \left( z^{2}+a^{2}\right) ^{-\frac {1}{2}}-1 \right\} \\[ 5pt ]
&=&-\frac {\sigma }{2\varepsilon _{0}}\left( \frac {z}{\sqrt{z^{2}+a^{2}}}-1 \right) \\[ 5pt ]
&=&\frac {\sigma }{2\varepsilon _{0}}\left( 1-\frac {z}{\sqrt {z^{2}+a^{2}}} \right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ハ
(3)の解答式の\( \ z \ \)を\( \ d-z \ \)にし,\( \ \sigma \ \)を\( \ -\sigma \ \)にすれば,点\( \ \mathrm {Q} \ \)が点\( \ \mathrm {P} \ \)に作る電界\( \ E_{\mathrm {z1}}^{\prime } \ \)が求められるので,
\[
\begin{eqnarray}
E_{\mathrm {z1}}^{\prime }&=&-\frac {\sigma }{2\varepsilon _{0}}\left( 1-\frac {d-z}{\sqrt {\left( d-z\right) ^{2}+a^{2}}} \right) \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,点\( \ \mathrm {P} \ \)の\( \ z \ \)方向電界\( \ E_{\mathrm {z2}} \ \)は,どちらも電界の向きが上向きであることに注意すると,
\[
\begin{eqnarray}
E_{\mathrm {z2}}&=&E_{\mathrm {z1}}-E_{\mathrm {z1}}^{\prime } \\[ 5pt ]
&=&\frac {\sigma }{2\varepsilon _{0}}\left( 1-\frac {z}{\sqrt {z^{2}+a^{2}}} \right) +\frac {\sigma }{2\varepsilon _{0}}\left\{ 1-\frac {d-z}{\sqrt {\left( d-z\right) ^{2}+a^{2}}} \right\} \\[ 5pt ]
&=&\frac {\sigma }{2\varepsilon _{0}}\left\{ 2-\frac {z}{\sqrt {z^{2}+a^{2}}}-\frac {d-z}{\sqrt {\left( d-z\right) ^{2}+a^{2}}}\right\} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:イ
(4)の解答式において,\( \ a≫d,z \ \)とすると,
\[
\begin{eqnarray}
E_{\mathrm {z2}}&=&\frac {\sigma }{2\varepsilon _{0}}\left\{ 2-\frac {z}{\sqrt {z^{2}+a^{2}}}-\frac {d-z}{\sqrt {\left( d-z\right) ^{2}+a^{2}}}\right\} \\[ 5pt ]
&≃&\frac {\sigma }{2\varepsilon _{0}}\left( 2-\frac {z}{a}-\frac {d-z}{a}\right) \\[ 5pt ]
&=&\frac {\sigma }{2\varepsilon _{0}}\left( 2-\frac {d}{a}\right) \\[ 5pt ]
&≃&\frac {\sigma }{2\varepsilon _{0}}\times 2 \\[ 5pt ]
&=&\frac {\sigma }{\varepsilon _{0}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん