《理論》〈電磁気〉[R03:問1]誘電体の近くに存在する電荷による界面の状態に関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，誘電体の近くに存在する電荷に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

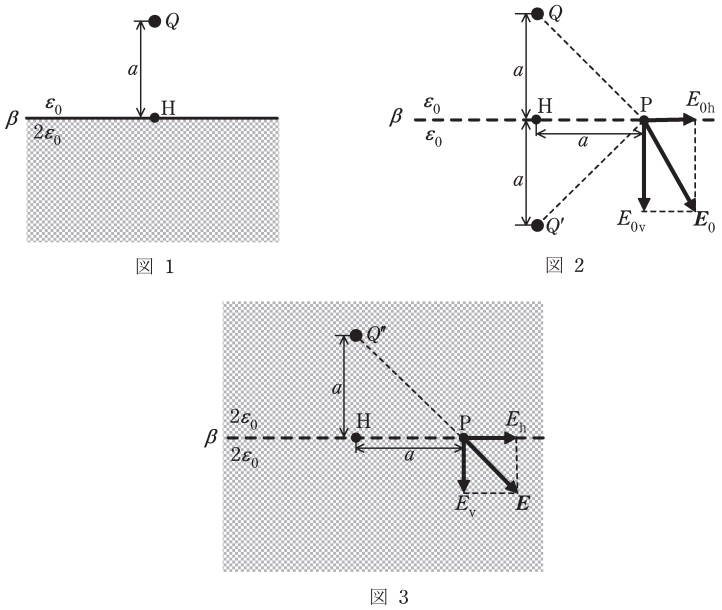
図1のように，平面$ \ \beta \ $から上方に距離$ \ a \ $離れた真空中に点電荷$ \ Q \ $を置く。$ \ \beta \ $より上側は誘電率$ \ \varepsilon _{0} \ $の真空であり，下側は誘電率$ \ 2\varepsilon _{0} \ $の誘電体で完全に満たされている。このとき，空間中の電界を求めるために，影像電荷の考え方を用いる。

$ \ \beta \ $より上側の電界は，図2のように，誘電体を取り除き，$ \ \beta \ $に対して電荷$ \ Q \ $と対称な位置に電荷$ \ Q^{\prime } \ $を置くことで求める。$ \ \beta \ $より下側の電界は，図3のように，全空間を誘電体で満たし，電荷$ \ Q \ $の位置の電荷を$ \ Q^{\prime \prime } \ $とすることで求める。

$ \ Q^{\prime } \ $及び$ \ Q^{\prime \prime } \ $は，$ \ \beta \ $上の任意の点において，$ \ \beta \ $に平行な電界の成分が同じであることと，$ \ \beta \ $に$ \ \fbox {　（１）　} \ $な電束密度の成分が同じであることにより求められる。ただし，ここでは簡単のため，電荷$ \ Q \ $より$ \ \beta \ $に下ろした垂線の足$ \ \mathrm {H} \ $から距離$ \ a \ $離れた点$ \ \mathrm {P} \ $を考える。

図2で，電荷$ \ Q \ $と$ \ Q^{\prime } \ $が点$ \ \mathrm {P} \ $に作る電界$ \ E_{0} \ $において，$ \ \beta \ $に平行な成分$ \ E_{\mathrm {0h}} \ $と垂直な成分$ \ E_{\mathrm {0v}} \ $はそれぞれ
\[
\begin{eqnarray}
E_{\mathrm {0h}}&=&\frac {Q+Q^{\prime }}{8\sqrt {2}\pi \varepsilon _{0} a^{2}}，E_{\mathrm {0v}}&=& \ \fbox {　（２）　} \\[ 5pt ] \end{eqnarray}
\] である。ただし，$ \ E_{\mathrm {0h}} \ $と$ \ E_{\mathrm {0v}} \ $は，それぞれ点$ \ \mathrm {H} \ $から点$ \ \mathrm {P} \ $へ向かう方向と誘電体に進入する方向を正とする。また，図3で，電荷$ \ Q^{\prime \prime } \ $が点$ \ \mathrm {P} \ $に作る電界$ \ \boldsymbol E \ $において，$ \ \beta \ $に平行な成分$ \ E_{\mathrm {h}} \ $と垂直な成分$ \ E_{\mathrm {v}} \ $はそれぞれ，
\[
\begin{eqnarray}
E_{\mathrm {h}}&=&E_{\mathrm {v}}&=& \frac {Q^{\prime \prime }}{4\pi \cdot 2\varepsilon _{0} \cdot 2a^{2}}\cdot \frac {1}{\sqrt {2}}&=&\frac {Q^{\prime \prime }}{16\sqrt {2}\pi \varepsilon _{0} a^{2}} \\[ 5pt ] \end{eqnarray}
\] である。ただし，$ \ E_{\mathrm {h}} \ $と$ \ E_{\mathrm {v}} \ $の向きの定義は，$ \ E_{\mathrm {0h}} \ $と$ \ E_{\mathrm {0v}} \ $と同様である。
ここで，$ \ \beta \ $に平行な電界の成分が同じであることにより$ \ E_{\mathrm {0h}}=E_{\mathrm {h}} \ $が成り立ち，$ \ \beta \ $に$ \ \fbox {　（１）　} \ $な電束密度の成分が同じであることにより，$ \ \fbox {　（３）　} \ $が成り立つ。これらから導かれる方程式を解くことで，置くべき影像電荷$ \ Q^{\prime } \ $と$ \ Q^{\prime \prime } \ $をそれぞれ$ \ \fbox {　（４）　} \ $，$ \ \fbox {　（５）　} \ $と定められる。

〔問1の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {E_{\mathrm {0v}}}{\varepsilon _{0}}=\frac {E_{\mathrm {v}}}{2\varepsilon _{0}}　　　　　&（ロ）&　\frac {\displaystyle \frac {QQ^{\prime }}{Q+Q^{\prime }}}{8\sqrt {2}\pi \varepsilon _{0} a^{2}}　　　　　&（ハ）&　2Q \\[ 5pt ] &（ニ）&　\frac {2}{3}Q　　　　　&（ホ）&　-\frac {1}{3}Q　　　　　&（ヘ）&　\varepsilon _{0}E_{\mathrm {0h}}=2\varepsilon _{0}E_{\mathrm {h}} \\[ 5pt ] &（ト）&　\frac {Q+Q^{\prime }}{8\sqrt {2}\pi \varepsilon _{0} a^{2}}　　　　　&（チ）&　0　　　　　&（リ）&　\frac {E_{\mathrm {0h}}}{\varepsilon _{0}}=\frac {E_{\mathrm {h}}}{2\varepsilon _{0}} \\[ 5pt ] &（ヌ）&　垂直　　　　　&（ル）&　平行　　　　　&（ヲ）&　\varepsilon _{0}E_{\mathrm {0v}}=2\varepsilon _{0}E_{\mathrm {v}} \\[ 5pt ] &（ワ）&　\frac {4}{3}Q　　　　　&（カ）&　-Q　　　　　&（ヨ）&　\frac {Q-Q^{\prime }}{8\sqrt {2}\pi \varepsilon _{0} a^{2}} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

誘電体の近くの電界に関する問題です。
問題文で解法を記載し，受験生にその場で考えさせるいかにも$ \ 1 \ $種らしい問題です。
解答では電界をガウスの定理を使用して求めていますが，途中$ \ E_{\mathrm {0h}} \ $，$ \ E_{\mathrm {h}} \ $及び$ \ E_{\mathrm {v}} \ $が与えられていることから，そこをヒントとして導出しても問題ないかと思います。

1.ガウスの定理
誘電率$ \ \varepsilon \ \mathrm {[F/m]} \ $の空間において，$ \ Q \ [ \mathrm {C} ] \ $から出る電気力線は$ \ \displaystyle \frac {Q}{\varepsilon } \ $本，電束は$ \ Q \ [ \mathrm {C} ] \ $であり，電束密度$ \ D \ \mathrm {[C/m^{2}]} \ $及び電界$ \ E \ \mathrm {[V/m]} \ $との関係は，任意の閉曲面において，
\[
\begin{eqnarray}
\int _{S} \boldsymbol D \cdot \mathrm {d}\boldsymbol S &=& Q \\[ 5pt ] \int _{S} \boldsymbol E \cdot \mathrm {d}\boldsymbol S &=& \frac {Q}{\varepsilon } \\[ 5pt ] \end{eqnarray}
\] となります。

2.点電荷が作る電界の強さ$ \ E \ $
ガウスの定理より，真空中（誘電率$ \ \varepsilon _{0} \ $）で点電荷$ \ Q \ $が作る電界の大きさ$ \ E \ $は，距離$ \ r \ $の地点で，
\[
\begin{eqnarray}
E&=&\frac {Q}{4\pi \varepsilon _{0}r^{2}} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)解答：ヌ
ワンポイント解説「1.ガウスの定理」の通り，点電荷$ \ Q \ $から出た電束は$ \ Q \ $であり，誘電率の変化による電束の増減は発生しないため，$ \ \beta \ $に垂直な電束密度の成分は同じである必要がある。

(2)解答：ヨ
図2において，電荷$ \ Q \ $が点$ \ \mathrm {P} \ $に作る電界$ \ E_{\mathrm {0Q}} \ $は，ワンポイント解説「2.点電荷が作る電界の強さ$ \ E \ $」の通り，
\[
\begin{eqnarray}
E_{\mathrm {0Q}}&=&\frac {Q}{4\pi \varepsilon _{0}\left( \sqrt {a^{2}+a^{2}}\right) ^{2}} \\[ 5pt ] &=&\frac {Q}{8\pi \varepsilon _{0}a^{2}} \\[ 5pt ] \end{eqnarray}
\] であり，その水平成分$ \ E_{\mathrm {0Qh}} \ $及び垂直成分$ \ E_{\mathrm {0Qv}} \ $は，
\[
\begin{eqnarray}
E_{\mathrm {0Qh}}&=&E_{\mathrm {0Q}}\cdot \frac {a}{\sqrt {a^{2}+a^{2}}} \\[ 5pt ] &=&\frac {Q}{8\pi \varepsilon _{0}a^{2}}\cdot \frac {1}{\sqrt {2}} \\[ 5pt ] &=&\frac {Q}{8\sqrt {2}\pi \varepsilon _{0}a^{2}} \\[ 5pt ] E_{\mathrm {0Qv}}&=&E_{\mathrm {0Q}}\cdot \frac {a}{\sqrt {a^{2}+a^{2}}} \\[ 5pt ] &=&\frac {Q}{8\pi \varepsilon _{0}a^{2}}\cdot \frac {1}{\sqrt {2}} \\[ 5pt ] &=&\frac {Q}{8\sqrt {2}\pi \varepsilon _{0}a^{2}} \\[ 5pt ] \end{eqnarray}
\] となる。同様に，電荷$ \ Q^{\prime } \ $が点$ \ \mathrm {P} \ $に作る電界$ \ E_{\mathrm {0Q^{\prime }}} \ $の水平成分$ \ E_{\mathrm {0Q^{\prime }h}} \ $及び垂直成分$ \ E_{\mathrm {0Q^{\prime }v}} \ $は，符号に注意すると，
\[
\begin{eqnarray}
E_{\mathrm {0Q^{\prime }h}}&=&\frac {Q^{\prime }}{8\sqrt {2}\pi \varepsilon _{0}a^{2}} \\[ 5pt ] E_{\mathrm {0Q^{\prime }v}}&=&-\frac {Q^{\prime }}{8\sqrt {2}\pi \varepsilon _{0}a^{2}} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，求める平行成分$ \ E_{\mathrm {0h}} \ $及び垂直成分$ \ E_{\mathrm {0v}} \ $は，
\[
\begin{eqnarray}
E_{\mathrm {0h}}&=&E_{\mathrm {0Qh}}+E_{\mathrm {0Q^{\prime }h}} \\[ 5pt ] &=&\frac {Q}{8\sqrt {2}\pi \varepsilon _{0}a^{2}}+\frac {Q^{\prime }}{8\sqrt {2}\pi \varepsilon _{0}a^{2}} \\[ 5pt ] &=&\frac {Q+Q^{\prime }}{8\sqrt {2}\pi \varepsilon _{0} a^{2}} \\[ 5pt ] E_{\mathrm {0v}}&=&E_{\mathrm {0Qv}}+E_{\mathrm {0Q^{\prime }v}} \\[ 5pt ] &=&\frac {Q}{8\sqrt {2}\pi \varepsilon _{0}a^{2}}-\frac {Q^{\prime }}{8\sqrt {2}\pi \varepsilon _{0}a^{2}} \\[ 5pt ] &=&\frac {Q-Q^{\prime }}{8\sqrt {2}\pi \varepsilon _{0} a^{2}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ヲ
(1)より，電束密度の垂直成分が等しいことから，
\[
\begin{eqnarray}
D_{\mathrm {0v}}&=&D_{\mathrm {v}} \\[ 5pt ] \varepsilon _{0}E_{\mathrm {0v}}&=&2\varepsilon _{0}E_{\mathrm {v}} \\[ 5pt ] \end{eqnarray}
\] が成立する。

(4)解答：ホ
図3において，平行成分$ \ E_{\mathrm {h}} \ $及び垂直成分$ \ E_{\mathrm {v}} \ $は，(2)と同様に，
\[
\begin{eqnarray}
E_{\mathrm {h}}&=&\frac {Q^{\prime \prime }}{8\sqrt {2}\pi \cdot 2\varepsilon _{0}a^{2}} \\[ 5pt ] &=&\frac {Q^{\prime \prime }}{16\sqrt {2}\pi \varepsilon _{0}a^{2}} \\[ 5pt ] E_{\mathrm {v}}&=&\frac {Q^{\prime \prime }}{8\sqrt {2}\pi \cdot 2\varepsilon _{0}a^{2}} \\[ 5pt ] &=&\frac {Q^{\prime \prime }}{16\sqrt {2}\pi \varepsilon _{0}a^{2}} \\[ 5pt ] \end{eqnarray}
\] であるから，$ \ E_{\mathrm {0h}}=E_{\mathrm {h}} \ $より，
\[
\begin{eqnarray}
\frac {Q+Q^{\prime }}{8\sqrt {2}\pi \varepsilon _{0} a^{2}}&=&\frac {Q^{\prime \prime }}{16\sqrt {2}\pi \varepsilon _{0}a^{2}} \\[ 5pt ] \frac {Q+Q^{\prime }}{8}&=&\frac {Q^{\prime \prime }}{16} \\[ 5pt ] 2\left( Q+Q^{\prime }\right) &=&Q^{\prime \prime }　・・・・・・・・・・　① \\[ 5pt ] \end{eqnarray}
\] となり，$ \ \varepsilon _{0}E_{\mathrm {0v}}=2\varepsilon _{0}E_{\mathrm {v}} \ $より，
\[
\begin{eqnarray}
\varepsilon _{0}\frac {Q-Q^{\prime }}{8\sqrt {2}\pi \varepsilon _{0} a^{2}}&=&2\varepsilon _{0}\frac {Q^{\prime \prime }}{16\sqrt {2}\pi \varepsilon _{0}a^{2}} \\[ 5pt ] Q-Q^{\prime } &=&Q^{\prime \prime }　・・・・・・・・・　② \\[ 5pt ] \end{eqnarray}
\] となる。②を①に代入すると，
\[
\begin{eqnarray}
2\left( Q+Q^{\prime }\right) &=&Q-Q^{\prime } \\[ 5pt ] 3Q^{\prime } &=&-Q \\[ 5pt ] Q^{\prime } &=&-\frac {1}{3}Q \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ワ
(4)解答式を②に代入すると，
\[
\begin{eqnarray}
Q^{\prime \prime }&=&Q-Q^{\prime } \\[ 5pt ] &=&Q-\left( -\frac {1}{3}Q\right) \\[ 5pt ] &=&\frac {4}{3}Q \\[ 5pt ] \end{eqnarray}
\] と求められる。