【問題】
【難易度】★★☆☆☆(やや易しい)
次の文章は,半導体の熱電効果に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
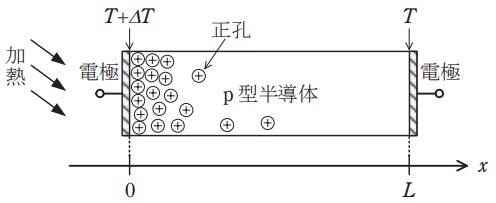
図のように,両端に電極を取り付けた長さ\( \ L \ \)の\( \ \mathrm {p} \ \)型半導体を考える。電極端子は開放とする。ここで,左端の電極を加熱したところ,\( \ x=0 \ \)における半導体の温度が\( \ T+\mathit {\Delta } T \ \left( \mathit {\Delta } T>0 \right) \ \)に上昇し,右端\( \ \left( x=L\right) \ \)における温度は\( \ T \ \)で定常状態になった。左端の温度上昇に伴い,\( \ x=0 \ \)における正孔濃度が増大することで濃度勾配が生じ,正孔が\( \ x \ \)軸の正の方向に拡散する。その結果,右端電極の電位が左端電極に対して\( \ \mathit {\Delta } V \ \)だけ上昇する。このように温度差\( \ \mathit {\Delta } T \ \)が生じることによって電位差\( \ \mathit {\Delta } V \ \)が発生する現象を\( \ \fbox { (1) } \ \)効果と呼び,\( \ \displaystyle \frac {\mathit {\Delta } V}{\mathit {\Delta } T} \ \)は\( \ \fbox { (1) } \ \)係数と呼ばれる。以下でこの係数を求めよう。
半導体内の位置\( \ x \ \)における正孔濃度を\( \ p \ \),拡散定数を\( \ D_{h} \ \),正孔の電荷量を\( \ e \ \left( >0 \right) \ \)とすると,正孔による拡散電流密度は,
\[
\begin{eqnarray}
&&-eD_{h}\frac {\mathrm {d}p}{\mathrm {d}x} \ ・・・・・・・・・・・・・・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
と表される。また,半導体内の電界を\( \ E \ \),正孔の移動度を\( \ \mu _{h} \ \)とすると,正孔によるドリフト電流密度は,
\[
\begin{eqnarray}
&&ep\mu _{h}E ・・・・・・・・・・・・・・・・・・・・・・・・ ② \\[ 5pt ]
\end{eqnarray}
\]
と表される。ただし\( \ E \ \)は,\( \ x \ \)軸の正方向を正にとるものとする。\( \ \mathrm {p} \ \)型半導体では電子濃度は小さいので電子電流の寄与は無視し,電界\( \ E \ \)は半導体内で一定と仮定する。この場合\( \ E \ \)は,\( \ \mathit {\Delta } V \ \)と\( \ L \ \)を用いて,\( \ E=- \ \fbox { (2) } \ \)と表される。両端子が開放されている場合,①式と②式で表される電流密度の総和は\( \ 0 \ \)となることから,
\[
\begin{eqnarray}
\frac {\mathrm {d}p}{\mathrm {d}x}&=&- \ \fbox { (3) } \ p ・・・・・・・・・・・・・・・・・・ ③ \\[ 5pt ]
\end{eqnarray}
\]
が得られる。ただしアインシュタインの関係式\( \ \displaystyle D_{h}=\frac {k_{\mathrm {B}}T}{e}\mu _{h} \ \)と\( \ \fbox { (2) } \ \)を用いて,\( \ \fbox { (3) } \ \)を\( \ D_{h} \ \),\( \ \mu _{h} \ \),\( \ E \ \)を用いずに表した。なお\( \ k_{\mathrm {B}} \ \)はボルツマン定数を表す。
一方,\( \ p \ \)は温度\( \ T \ \)の関数でもあるから,\( \ \displaystyle \frac {\mathrm {d}p}{\mathrm {d}x}=\frac {\mathrm {d}p}{\mathrm {d}T}\frac {\mathrm {d}T}{\mathrm {d}x} \ \)と表される。\( \ \mathit {\Delta }T \ \)を十分小さいと仮定して\( \ \displaystyle \frac {\mathrm {d}T}{\mathrm {d}x}≈-\frac {\mathit {\Delta }T}{L} \ \)を代入すると,
\[
\begin{eqnarray}
\frac {\mathrm {d}p}{\mathrm {d}x}&=&-\frac {\mathrm {d}p}{\mathrm {d}T}\frac {\mathit {\Delta }T}{L} \ ・・・・・・・・・・・・・・・・・・・ ④ \\[ 5pt ]
\end{eqnarray}
\]
③式と④式の右辺が等しいとおいた式から,\( \ \displaystyle \frac {\mathit {\Delta } V}{\mathit {\Delta } T} \ \)を求めると,
\[
\begin{eqnarray}
\frac {\mathit {\Delta } V}{\mathit {\Delta } T} &=& \ \fbox { (4) } \ \frac {1}{p}\frac {\mathrm {d}p}{\mathrm {d}T} ・・・・・・・・・・・・・・・・ ⑤ \\[ 5pt ]
\end{eqnarray}
\]
正孔濃度\( \ p \ \)と温度\( \ T \ \)の関係は,次のように与えられる。
\[
\begin{eqnarray}
p &=& UT^{\frac {3}{2}}\mathrm {exp}\left( -\frac {eV_{\mathrm {F}}}{k_{\mathrm {B}}T}\right) \ ・・・・・・・・・・・・・・・ ⑥ \\[ 5pt ]
\end{eqnarray}
\]
ただし,\( \ U \ \),\( \ V_{\mathrm {F}} \ \)は定数と仮定する。⑥式を⑤式に代入すると,\( \ \displaystyle \frac {\mathit {\Delta } V}{\mathit {\Delta } T} = \ \fbox { (5) } \ +\frac {V_{\mathrm {F}}}{T} \ \)が得られる。
〔問6の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {k_{\mathrm {B}}T}{e}\frac {L}{\mathit {\Delta }V} &(ロ)& \frac {2}{3}\frac {e}{k_{\mathrm {B}}} &(ハ)& \frac {L}{\mathit {\Delta }V} \\[ 5pt ]
&(ニ)& \frac {e}{k_{\mathrm {B}}T} &(ホ)& \frac {3}{2}\frac {k_{\mathrm {B}}}{e} &(ヘ)& ゼーベック \\[ 5pt ]
&(ト)& \frac {e}{k_{\mathrm {B}}T}\frac {\mathit {\Delta }V}{L} &(チ)& トムソン &(リ)& ek_{\mathrm {B}}T \\[ 5pt ]
&(ヌ)& L\cdot \mathit {\Delta }V &(ル)& ペルチェ &(ヲ)& \frac {\mathit {\Delta }V}{L} \\[ 5pt ]
&(ワ)& \frac {2}{3}\frac {k_{\mathrm {B}}}{e} &(カ)& \frac {k_{\mathrm {B}}T}{e}\frac {\mathit {\Delta }V}{L} &(ヨ)& \frac {k_{\mathrm {B}}T}{e} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
半導体の熱電効果に関する問題です。
(1)は知識問題ですが,(2)以降はその場で読解しながら計算していく問題です。
(5)の微分の計算がやや計算量が多いですが,微分積分は\( \ 1 \ \)種においては使いこなせるレベルに到達する必要がありますので,きちんと基礎から復習するようにしましょう。
1.ペルチェ効果
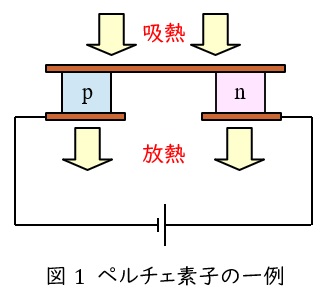
異なる金属や半導体を接合して,電圧をかけると,吸熱もしくは発熱を発生する現象です。図1が代表的な半導体を使用したペルチェ素子で,電流の向きを逆にすると,発熱と吸熱も入れ替わります。
2.ゼーベック効果
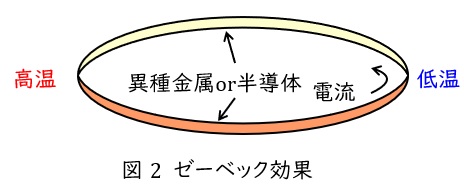
異なる金属や半導体を図2のように接合して閉回路を作り,一端を高温(温接点),もう一端を低温(冷接点)とすると,熱起電力が発生し電流が流れる現象を言います。
【解答】
(1)解答:ヘ
題意より解答候補は,(ヘ)ゼーベック,(チ)トムソン,(ル)ペルチェ,になると思います。
ワンポイント解説「2.ゼーベック効果」の通り,温度差が生じることによって電位差が発生する現象をゼーベック効果といいます。
(2)解答:ヲ
電界\( \ E \ \)は,電位差\( \ \mathit {\Delta } V \ \)と長さ\( \ L \ \)で表すと,
\[
\begin{eqnarray}
E &=& -\frac {\mathit {\Delta } V}{L} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ト
題意より,①式と②式で表される電流密度の総和は\( \ 0 \ \)であるから,
\[
\begin{eqnarray}
-eD_{h}\frac {\mathrm {d}p}{\mathrm {d}x}+ep\mu _{h}E &=&0 \\[ 5pt ]
eD_{h}\frac {\mathrm {d}p}{\mathrm {d}x} &=&ep\mu _{h}E \\[ 5pt ]
D_{h}\frac {\mathrm {d}p}{\mathrm {d}x} &=&p\mu _{h}E \\[ 5pt ]
\end{eqnarray}
\]
となり,これに\( \ \displaystyle D_{h}=\frac {k_{\mathrm {B}}T}{e}\mu _{h} \ \)及び\( \ \displaystyle E = -\frac {\mathit {\Delta } V}{L} \ \)を代入すると,
\[
\begin{eqnarray}
\frac {k_{\mathrm {B}}T}{e}\mu _{h}\frac {\mathrm {d}p}{\mathrm {d}x} &=&p\mu _{h}\left( -\frac {\mathit {\Delta } V}{L}\right) \\[ 5pt ]
\frac {k_{\mathrm {B}}T}{e}\frac {\mathrm {d}p}{\mathrm {d}x} &=&-\frac {\mathit {\Delta } V}{L}p \\[ 5pt ]
\frac {\mathrm {d}p}{\mathrm {d}x} &=&-\frac {e}{k_{\mathrm {B}}T}\frac {\mathit {\Delta } V}{L}p \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ヨ
(3)解答式に④式を代入すると,
\[
\begin{eqnarray}
-\frac {\mathrm {d}p}{\mathrm {d}T}\frac {\mathit {\Delta }T}{L} &=&-\frac {e}{k_{\mathrm {B}}T}\frac {\mathit {\Delta } V}{L}p \\[ 5pt ]
\frac {\mathrm {d}p}{\mathrm {d}T}\mathit {\Delta }T &=&\frac {e}{k_{\mathrm {B}}T}\mathit {\Delta } Vp \\[ 5pt ]
\frac {\mathit {\Delta } V}{\mathit {\Delta } T} &=& \frac {k_{\mathrm {B}}T}{e} \frac {1}{p}\frac {\mathrm {d}p}{\mathrm {d}T} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ホ
⑥式より\( \ \displaystyle \frac {\mathrm {d}p}{\mathrm {d}T} \ \)は,
\[
\begin{eqnarray}
\frac {\mathrm {d}p}{\mathrm {d}T} &=&U\cdot \frac {3}{2}T^{\frac {1}{2}}\mathrm {exp}\left( -\frac {eV_{\mathrm {F}}}{k_{\mathrm {B}}T}\right) +UT^{\frac {3}{2}}\left( \frac {eV_{\mathrm {F}}}{k_{\mathrm {B}}T^{2}}\right) \mathrm {exp}\left( -\frac {eV_{\mathrm {F}}}{k_{\mathrm {B}}T}\right) \\[ 5pt ]
&=&\frac {3}{2}UT^{\frac {1}{2}}\mathrm {exp}\left( -\frac {eV_{\mathrm {F}}}{k_{\mathrm {B}}T}\right) +UT^{\frac {1}{2}}\left( \frac {eV_{\mathrm {F}}}{k_{\mathrm {B}}T}\right) \mathrm {exp}\left( -\frac {eV_{\mathrm {F}}}{k_{\mathrm {B}}T}\right) \\[ 5pt ]
&=&UT^{\frac {1}{2}}\mathrm {exp}\left( -\frac {eV_{\mathrm {F}}}{k_{\mathrm {B}}T}\right) \left( \frac {3}{2}+ \frac {eV_{\mathrm {F}}}{k_{\mathrm {B}}T} \right) \\[ 5pt ]
\end{eqnarray}
\]
となるので,これと⑥式を(4)解答式に代入すると,
\[
\begin{eqnarray}
\frac {\mathit {\Delta } V}{\mathit {\Delta } T} &=& \frac {k_{\mathrm {B}}T}{e} \frac {1}{\displaystyle UT^{\frac {3}{2}}\mathrm {exp}\left( -\frac {eV_{\mathrm {F}}}{k_{\mathrm {B}}T}\right)}UT^{\frac {1}{2}}\mathrm {exp}\left( -\frac {eV_{\mathrm {F}}}{k_{\mathrm {B}}T}\right) \left( \frac {3}{2}+ \frac {eV_{\mathrm {F}}}{k_{\mathrm {B}}T} \right) \\[ 5pt ]
&=& \frac {k_{\mathrm {B}}}{e} \left( \frac {3}{2}+\frac {eV_{\mathrm {F}}}{k_{\mathrm {B}}T} \right) \\[ 5pt ]
&=& \frac {3}{2}\frac {k_{\mathrm {B}}}{e} +\frac {V_{\mathrm {F}}}{T} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん