【問題】
【難易度】★★★☆☆(普通)
次の文章は,電気回路の過渡現象に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
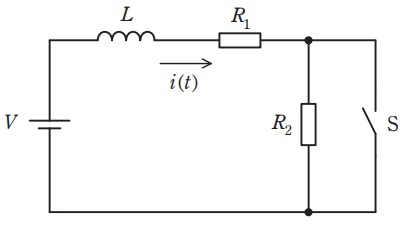
図の回路において,時刻\( \ t<0 \ \)ではスイッチ\( \ \mathrm {S} \ \)は開いており,回路は定常状態にある。この回路において,図に示すように回路の電流を\( \ i \left( t\right) \ \)とし,\( \ t=0 \ \)でスイッチ\( \ \mathrm {S} \ \)を閉じるものとすると,\( \ t≧0 \ \)においては次式の回路方程式が成り立つ。
\[
\begin{eqnarray}
L\frac {\mathrm {d}i \left( t\right) }{\mathrm {d}t}+R_{1} i (t) &=&V ・・・・・・・・・・・・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
スイッチ\( \ \mathrm {S} \ \)を閉じた直後の回路の電流を\( \ i \left( 0\right) \ \)とし,①式の両辺をラプラス変換すれば,次式を得る。ただし,\( \ i \left( t\right) \ \)のラプラス変換を\( \ I \left( s\right) \ \)と表記する。
\[
\begin{eqnarray}
\ \fbox { (1) } \ &=&\frac {V}{s} ・・・・・・・・・・・・・・・・・・・・・・・・ ② \\[ 5pt ]
\end{eqnarray}
\]
ここで,\( \ i \left( 0\right) = \ \fbox { (2) } \ \)であることから,ラプラス変換された回路方程式である②式より,次式を得る。
\[
\begin{eqnarray}
I \left( s\right) &=& \ \fbox { (3) } \ +\frac {L}{sL+R_{1}}\cdot \frac {V}{R_{1}+R_{2}} ・・・・・・・・・・・ ③ \\[ 5pt ]
\end{eqnarray}
\]
③式の両辺を逆ラプラス変換すれば,\( \ t≧0 \ \)における\( \ i \left( t\right) \ \)は,次式となる。
\[
\begin{eqnarray}
i \left( t\right) &=& \ \fbox { (4) } \ +\frac {V}{R_{1}+R_{2}}\mathrm {e}^{-\frac {t}{\tau }} ・・・・・・・・・・・・・・・ ④ \\[ 5pt ]
\end{eqnarray}
\]
ただし,時定数\( \ \tau = \ \fbox { (5) } \ \)である。
〔問4の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {V}{R_{2}} &(ロ)& \frac {V}{R_{2}}\left( 1-\mathrm {e}^{-\frac {t}{\tau }}\right) &(ハ)& \frac {V}{R_{1}}\left( 1-\mathrm {e}^{-\frac {t}{\tau }}\right) \\[ 5pt ]
&(ニ)& \frac {L}{R_{1}} &(ホ)& \frac {V}{R_{1}+R_{2}}\left( 1-\mathrm {e}^{-\frac {t}{\tau }}\right) &(ヘ)& \frac {L}{R_{1}+R_{2}} \\[ 5pt ]
&(ト)& \frac {V}{R_{1}+R_{2}} &(チ)& \frac {R_{1}}{L} &(リ)& L\left[ sI \left( s\right) -I \left( s\right) \right] +R_{1}i \left( 0\right) \\[ 5pt ]
&(ヌ)& \frac {V}{R_{1}} &(ル)& \frac {V}{s\left( sL+R_{2}\right) } &(ヲ)& L\left[ sI \left( s\right) +i \left( 0\right) \right] +R_{1}I \left( s\right) \\[ 5pt ]
&(ワ)& \frac {V}{s\left( sL+R_{1}+R_{2}\right) } &(カ)& \frac {V}{s\left( sL+R_{1}\right) } &(ヨ)& L\left[ sI \left( s\right) -i \left( 0\right) \right] +R_{1}I \left( s\right) \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
過渡現象に関する問題ですが,問題でラプラス変換が指定されている珍しい問題です。
\( \ 1 \ \)種受験生の場合,十分に理解されている方も多いですが,ラプラス変換は自動制御の分野では必須の知識となりますので,必ず表を覚えておくようにしましょう。
1.基本的なラプラス変換
\( \ f(t) \ \)のラプラス変換を\( \ F(s) \ \)とすると以下のような関係があります。
\[
\begin{array}{|c|c|}
\hline
f(t) & F(s) \\
\hline
{\displaystyle \delta (t) }\atop{単位インパルス関数} & 1 \\[ 5pt ]
{\displaystyle u (t) }\atop{単位ステップ関数} & \displaystyle \frac {1}{s} \\[ 5pt ]
K & \displaystyle \frac {K}{s} \\[ 5pt ]
t & \displaystyle \frac {1}{s^{2}} \\[ 5pt ]
\mathrm {e}^{at} & \displaystyle \frac {1}{s-a} \\[ 5pt ]
\sin \omega t & \displaystyle \frac {\omega }{s^{2}+\omega ^{2}} \\[ 5pt ]
\cos \omega t & \displaystyle \frac {s}{s^{2}+\omega ^{2}} \\[ 5pt ]
\displaystyle \frac {\mathrm {d}f\left( t \right) }{\mathrm {d}t} & sF\left( s \right) -f\left( 0 \right) \\[ 5pt ]
\displaystyle \int f\left( t \right) \mathrm {d}t & \displaystyle \frac {F\left( s \right) }{s}+\frac {1}{s}\int _{-\infty }^{0}f\left( \tau \right) \mathrm {d}\tau \\[ 5pt ]
\hline
\end{array}
\]
【解答】
(1)解答:ヨ
①式の両辺をラプラス変換すると,ワンポイント解説「1.基本的なラプラス変換」の通り,
\[
\begin{eqnarray}
L\left[ sI \left( s\right) -i \left( 0\right) \right] +R_{1}I \left( s\right) &=&\frac {V}{s} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ト
スイッチ\( \ \mathrm {S} \ \)を閉じる直前において,回路は定常状態であるから,リアクトル\( \ L \ \)は短絡状態であると考えればよい。したがって,
\[
\begin{eqnarray}
i \left( 0\right) &=&\frac {V}{R_{1}+R_{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:カ
(1)及び(2)より,
\[
\begin{eqnarray}
L\left[ sI \left( s\right) -\frac {V}{R_{1}+R_{2}} \right] +R_{1}I \left( s\right) &=&\frac {V}{s} \\[ 5pt ]
\end{eqnarray}
\]
であるから,これを\( \ I \left( s\right) \ \)について整理すると,
\[
\begin{eqnarray}
LsI \left( s\right) -\frac {LV}{R_{1}+R_{2}} +R_{1}I \left( s\right) &=&\frac {V}{s} \\[ 5pt ]
LsI \left( s\right) +R_{1}I \left( s\right) &=&\frac {V}{s}+\frac {LV}{R_{1}+R_{2}} \\[ 5pt ]
\left( Ls+R_{1}\right) I \left( s\right) &=&\frac {V}{s}+\frac {LV}{R_{1}+R_{2}} \\[ 5pt ]
I \left( s\right) &=& \frac {V}{s\left( Ls+R_{1}\right) } +\frac {LV}{\left( Ls+R_{1}\right) \left( R_{1}+R_{2}\right) } \\[ 5pt ]
&=& \frac {V}{s\left( sL+R_{1}\right) } +\frac {L}{sL+R_{1}}\cdot \frac {V}{R_{1}+R_{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ハ
(3)解答式の分母分子を\( \ L \ \)で割ると,
\[
\begin{eqnarray}
I \left( s\right) &=& \frac {\displaystyle \frac {V}{L}}{\displaystyle s\left( s+\frac {R_{1}}{L}\right) } +\frac {1}{\displaystyle s+\frac {R_{1}}{L}}\cdot \frac {V}{R_{1}+R_{2}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,右辺第\( \ 1 \ \)項を部分分数分解することを考える。\( \ \frac {\displaystyle \frac {V}{L}}{\displaystyle s\left( s+\frac {R_{1}}{L}\right) } =\displaystyle \frac {A}{s}+\frac {\displaystyle B}{\displaystyle s+\frac {R_{1}}{L}} \ \)とおけば,
\[
\begin{eqnarray}
\frac {\displaystyle \frac {V}{L}}{\displaystyle s\left( s+\frac {R_{1}}{L}\right) } &=& \frac {\displaystyle A\left( s+\frac {R_{1}}{L}\right) +Bs }{\displaystyle s\left( s+\frac {R_{1}}{L}\right) } \\[ 5pt ]
&=& \frac {\displaystyle \left( A+B\right) s+A \frac {R_{1}}{L} }{\displaystyle s\left( s+\frac {R_{1}}{L}\right) } \\[ 5pt ]
\end{eqnarray}
\]
となるので,両辺を係数比較すると,
\[
\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle A + B = 0 \\
\displaystyle A \frac {R_{1}}{L} = \frac {V}{L}
\end{array}
\right. \\[ 5pt ]
\end{eqnarray}
\]
となる。この連立方程式を解けば\( \ \displaystyle A=\frac {V}{R_{1}} \ \)及び\( \ \displaystyle B=-\frac {V}{R_{1}} \ \)となるため,
\[
\begin{eqnarray}
I \left( s\right) &=& \frac {\displaystyle \frac {V}{R_{1}}}{s}-\frac {\displaystyle \frac {V}{R_{1}}}{\displaystyle s+\frac {R_{1}}{L}} +\frac {1}{\displaystyle s+\frac {R_{1}}{L}}\cdot \frac {V}{R_{1}+R_{2}} \\[ 5pt ]
\end{eqnarray}
\]
となり,両辺逆ラプラス変換すると,ワンポイント解説「1.基本的なラプラス変換」の通り,
\[
\begin{eqnarray}
i \left( t\right) &=& \frac {V}{R_{1}}-\frac {V}{R_{1}}\mathrm {e}^{-\frac {R_{1}}{L}t}+\frac {V}{R_{1}+R_{2}}\mathrm {e}^{-\frac {R_{1}}{L}t} \\[ 5pt ]
&=& \frac {V}{R_{1}}\left( 1-\mathrm {e}^{-\frac {R_{1}}{L}t}\right) +\frac {V}{R_{1}+R_{2}}\mathrm {e}^{-\frac {R_{1}}{L}t} \\[ 5pt ]
\end{eqnarray}
\]
となるため,\( \ \displaystyle \tau =\frac {L}{R_{1}} \ \)とおけば,
\[
\begin{eqnarray}
i \left( t\right) &=& \frac {V}{R_{1}}\left( 1-\mathrm {e}^{-\frac {t}{\tau }}\right) +\frac {V}{R_{1}+R_{2}}\mathrm {e}^{-\frac {t}{\tau }} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ニ
(4)解答式より,時定数\( \ \displaystyle \tau =\frac {L}{R_{1}} \ \)である。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん