【問題】
【難易度】★☆☆☆☆(易しい)
次の文章は,直流回路の消費電力に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
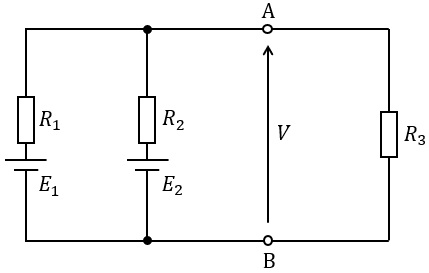
電圧\( \ E_{1} \ \),\( \ E_{2} \ \)の直流電圧源及び抵抗\( \ R_{1} \ \),\( \ R_{2} \ \),\( \ R_{3} \ \)で構成される回路における\( \ R_{3} \ \)の消費電力\( \ P \ \)を求めたい。図中の端子\( \ \mathrm {A-B} \ \)間の電圧を\( \ V \ \)とすれば,\( \ P=\displaystyle \frac {V^{2}}{R_{3}} \ \)なので,まずは\( \ V \ \)を求めてみる。
最初に,図の電圧源を短絡除去した回路を考えて,端子\( \ \mathrm {A-B} \ \)間から見た回路全体のコンダクタンスを求めると\( \ \fbox { (1) } \ \)となる。次に,図の端子\( \ \mathrm {A-B} \ \)間を短絡した回路を考えて,端子\( \ \mathrm {B} \ \)から\( \ R_{1} \ \)及び\( \ R_{2} \ \)を介して端子\( \ \mathrm {A} \ \)に流れる電流を求めると\( \ \fbox { (2) } \ \)となる。ここで,上記のように求めたコンダクタンス及び電流を用いて次式のように\( \ V \ \)を求めることができる。
\[
\begin{eqnarray}
V &=& \frac { \ \fbox { (2) } \ }{ \ \fbox { (1) } \ } \\[ 5pt ]
\end{eqnarray}
\]
このように,直列接続された電圧源と抵抗が複数並列接続された回路の電圧を求める定理は\( \ \fbox { (3) } \ \)の定理と呼ばれる。
次に,\( \ P \ \)が最大になるような\( \ R_{3} \ \)の値を求めてみる。消費電力が最大になるのは,図の電圧源を短絡除去した回路を考えて,端子\( \ \mathrm {A-B} \ \)から見た左側の合成抵抗が\( \ R_{3} \ \)と等しい場合である。したがって,\( \ R_{3}= \ \fbox { (4) } \ \)を満足するとき,最大電力が\( \ \fbox { (5) } \ \)となる。
〔問3の解答群〕
\[
\begin{eqnarray}
&(イ)& テブナン &(ロ)& ジュール &(ハ)& ミルマン \\[ 5pt ]
&(ニ)& \frac {R_{1}+R_{2}}{R_{1}R_{2}} &(ホ)& \frac {E_{2}}{R_{1}}+\frac {E_{1}}{R_{2}} &(ヘ)& \frac {E_{1}}{R_{1}}+\frac {E_{2}}{R_{2}} \\[ 5pt ]
&(ト)& \frac {R_{1}R_{2}}{R_{1}+R_{2}} &(チ)& \frac {1}{R_{1}}+\frac {1}{R_{2}}+\frac {1}{R_{3}} &(リ)& \frac {R_{3}}{R_{1}R_{2}} \\[ 5pt ]
&(ヌ)& R_{1}E_{1}+R_{2}E_{2} &(ル)& R_{1}+R_{2} &(ヲ)& R_{1}+R_{2}+R_{3} \\[ 5pt ]
&(ワ)& \frac {\left( R_{2}E_{1}+R_{1}E_{2}\right) ^{2}}{2R_{1}R_{2}\left( R_{1}+R_{2}\right) } &(カ)& \frac {\left( R_{2}E_{1}+R_{1}E_{2}\right) ^{2}}{4R_{1}R_{2}\left( R_{1}+R_{2}\right) } &(ヨ)& \frac {R_{2}E_{1}+R_{1}E_{2}}{4R_{1}R_{2}\left( R_{1}+R_{2}\right) } \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
直流電圧源と抵抗を直並列した回路の消費電力を求める問題です。
おそらく多くの受験生がノーヒントで解ける問題ですが,誘導に沿って解いていく必要があります。
試験全体の難易度を考えると,本問はぜひ完答を目指したい問題と言えるかと思います。
1.ミルマンの定理
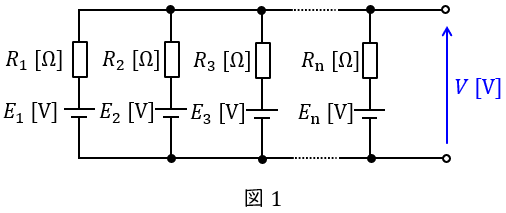
図1のような,電源\( \ E_{1} \ \mathrm {[V]} \ \),\( \ E_{2} \ \mathrm {[V]} \ \),\( \ \cdots \ \),\( \ E_{\mathrm {n}} \ \mathrm {[V]} \ \)と抵抗\( \ R_{1} \ \mathrm {[\Omega ]} \ \),\( \ R_{2} \ \mathrm {[\Omega ]} \ \),\( \ \cdots \ \),\( \ R_{\mathrm {n}} \ \mathrm {[\Omega ]} \ \)が直並列された回路における全体の電圧\( \ V \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
V&=&\frac {\displaystyle \frac {E_{1}}{R_{1}}+\frac {E_{2}}{R_{2}}+\frac {E_{3}}{R_{3}}+\cdots +\frac {E_{\mathrm {n}}}{R_{\mathrm {n}}}}{\displaystyle \frac {1}{R_{1}}+\frac {1}{R_{2}}+\frac {1}{R_{3}}+\cdots +\frac {1}{R_{\mathrm {n}}}} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。電源が繋がっていない場合は\( \ E=0 \ \mathrm {[V]} \ \),電源が逆向きの場合は\( \ -E \ \mathrm {[V]} \ \)とすればミルマンの定理はそのまま適用できます。
【解答】
(1)解答:チ
電圧源を短絡除去した回路において,端子\( \ \mathrm {A-B} \ \)間から見た回路全体のコンダクタンス\( \ G \ \)は,\( \ R_{1} \ \),\( \ R_{2} \ \),\( \ R_{3} \ \)の並列回路であるから,
\[
\begin{eqnarray}
G&=&\frac {1}{R_{1}}+\frac {1}{R_{2}}+\frac {1}{R_{3}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ヘ
図の端子\( \ \mathrm {A-B} \ \)間を短絡した回路を考えて,端子\( \ \mathrm {B} \ \)から\( \ R_{1} \ \)及び\( \ R_{2} \ \)を介して端子\( \ \mathrm {A} \ \)に流れる電流\( \ I \ \)は,
\[
\begin{eqnarray}
I&=&\frac {E_{1}}{R_{1}}+\frac {E_{2}}{R_{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ハ
ワンポイント解説「1.ミルマンの定理」の通り,直列接続された電圧源と抵抗が複数並列接続された回路の電圧を求める定理はミルマンの定理となる。
(4)解答:ト
図の電圧源を短絡除去した回路を考えて,端子\( \ \mathrm {A-B} \ \)から見た左側の合成抵抗\( \ R_{3} \ \)は,
\[
\begin{eqnarray}
R_{3}&=&\frac {R_{1}R_{2}}{R_{1}+R_{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:カ
(1),(2)及び(4)より,最大電力\( \ P \ \)は,
\[
\begin{eqnarray}
P&=&\frac {V^{2}}{R_{3}} \\[ 5pt ]
&=&\frac {\displaystyle \left( \frac {\displaystyle \frac {E_{1}}{R_{1}}+\frac {E_{2}}{R_{2}}}{\displaystyle \frac {1}{R_{1}}+\frac {1}{R_{2}}+\frac {1}{R_{3}}}\right) ^{2}}{\displaystyle \frac {R_{1}R_{2}}{R_{1}+R_{2}}} \\[ 5pt ]
&=&\frac {\displaystyle \left( \frac {\displaystyle \frac {E_{1}}{R_{1}}+\frac {E_{2}}{R_{2}}}{\displaystyle \frac {1}{R_{1}}+\frac {1}{R_{2}}+\frac {R_{1}+R_{2}}{R_{1}R_{2}}}\right) ^{2}}{\displaystyle \frac {R_{1}R_{2}}{R_{1}+R_{2}}} \\[ 5pt ]
&=&\left( \frac {\displaystyle \frac {E_{1}}{R_{1}}+\frac {E_{2}}{R_{2}}}{\displaystyle \frac {1}{R_{1}}+\frac {1}{R_{2}}+\frac {R_{1}+R_{2}}{R_{1}R_{2}}}\right) ^{2}\times \frac {R_{1}+R_{2}}{R_{1}R_{2}} \\[ 5pt ]
&=&\left( \frac {\displaystyle \frac {R_{2}E_{1}+R_{1}E_{2}}{R_{1}R_{2}}}{\displaystyle \frac {R_{2}+R_{1}+R_{1}+R_{2}}{R_{1}R_{2}}}\right) ^{2}\times \frac {R_{1}+R_{2}}{R_{1}R_{2}} \\[ 5pt ]
&=&\left\{ \frac { R_{2}E_{1}+R_{1}E_{2}}{2\left( R_{1}+R_{2}\right) }\right\} ^{2}\times \frac {R_{1}+R_{2}}{R_{1}R_{2}} \\[ 5pt ]
&=&\frac {\left( R_{2}E_{1}+R_{1}E_{2}\right) ^{2}}{4\left( R_{1}+R_{2}\right) ^{2}}\times \frac {R_{1}+R_{2}}{R_{1}R_{2}} \\[ 5pt ]
&=&\frac {\left( R_{2}E_{1}+R_{1}E_{2}\right) ^{2}}{4R_{1}R_{2}\left( R_{1}+R_{2}\right) } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん