【問題】
【難易度】★★☆☆☆(やや易しい)
次の文章は,三相交流回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
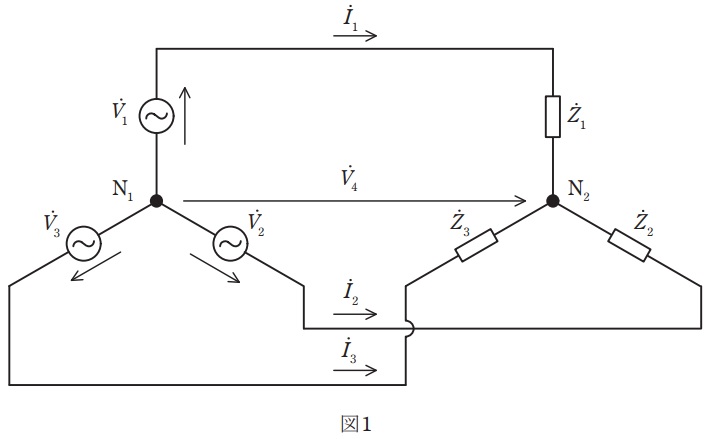
図1の回路は,不平衡三相電源に不平衡三相負荷が接続された\( \ \mathrm {Y} \ \)結線不平衡三相回路である。
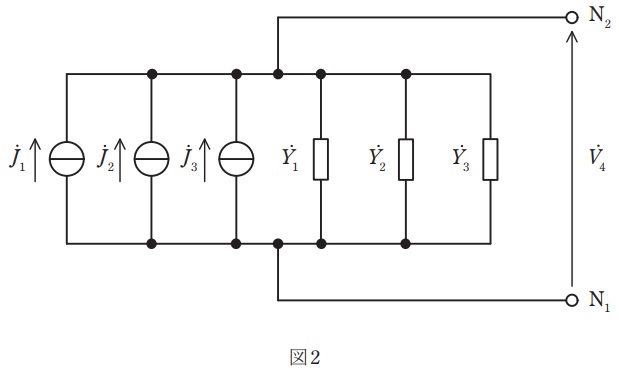
ミルマンの定理より,図1の回路は交流電流源\( \ {\dot J}_{1} \ \),\( \ {\dot J}_{2} \ \),\( \ {\dot J}_{3} \ \)及び三相負荷のアドミタンス\( \ \displaystyle {\dot Y}_{1}=\frac {1}{{\dot Z}_{1}} \ \),\( \ \displaystyle {\dot Y}_{2}=\frac {1}{{\dot Z}_{2}} \ \),\( \ \displaystyle {\dot Y}_{3}=\frac {1}{{\dot Z}_{3}} \ \)を用いて,図2に示す等価回路に変換できる。ただし,図2の等価回路において,交流電流源\( \ {\dot J}_{m}= \ \fbox { (1) } \ \),\( \ m=1,2,3 \ \)である。
図1の中性点\( \ {\mathrm {N}}_{1}-{\mathrm {N}}_{2} \ \)間の電圧を\( \ {\dot V}_{4} \ \)とすれば,図1の各相の線電流\( \ {\dot I}_{m}= \ \fbox { (2) } \ \),\( \ m=1,2,3 \ \)となる。また,図2の等価回路から電圧\( \ {\dot V}_{4}= \ \fbox { (3) } \ \)となる。ただし,電圧\( \ {\dot V}_{4} \ \)は図1及び図2の向きを正とする。
図1において,電源電圧を平衡三相である\( \ {\dot V}_{1}=100 \ \mathrm {V} \ \),\( \ {\dot V}_{2}=100\mathrm {e}^{-\mathrm {j}\frac {2}{3}\pi } \ \mathrm {[V]} \ \),\( \ {\dot V}_{3}=100\mathrm {e}^{-\mathrm {j}\frac {4}{3}\pi } \ \mathrm {[V]} \ \)とし,三相負荷のインピーダンス\( \ {\dot Z}_{1}=\mathrm {j} \ \mathrm {[\Omega ]} \ \),\( \ {\dot Z}_{2}=1 \ \mathrm {\Omega } \ \),\( \ {\dot Z}_{3}=1 \ \mathrm {\Omega } \ \)とする。このとき,中性点\( \ {\mathrm {N}}_{1}-{\mathrm {N}}_{2} \ \)間の電圧\( \ {\dot V}_{4}= \ \fbox { (4) } \ \mathrm {[V]} \ \)となる。なお,\( \ {\dot V}_{2}+{\dot V}_{3}= \ \fbox { (5) } \ \)となることに注意せよ。
〔問4の解答群〕
\[
\begin{eqnarray}
&(イ)& -\frac {100+\mathrm {j}100}{2+\mathrm {j}} &(ロ)& {\dot Y}_{m}{\dot V}_{m} &(ハ)& \left( {\dot V}_{m}-{\dot V}_{4}\right) {\dot Y}_{m} \\[ 5pt ]
&(ニ)& {\dot V}_{1}+{\dot V}_{2}+{\dot V}_{3} &(ホ)& \sqrt {{\dot Y}_{m}{\dot V}_{m}} &(ヘ)& -{\dot V}_{1} \\[ 5pt ]
&(ト)& \frac {{\dot Y}_{1}{\dot V}_{1}+{\dot Y}_{2}{\dot V}_{2}+{\dot Y}_{3}{\dot V}_{3}}{{\dot Y}_{1}+{\dot Y}_{2}+{\dot Y}_{3}} &(チ)& -\frac {100-\mathrm {j}100}{2-\mathrm {j}} &(リ)& {\dot V}_{1} \\[ 5pt ]
&(ヌ)& \left( {\dot V}_{1}+{\dot V}_{2}+{\dot V}_{3}\right) {\dot Y}_{m} &(ル)& 0 &(ヲ)& \left( {\dot V}_{m}+{\dot V}_{4}\right) {\dot Y}_{m} \\[ 5pt ]
&(ワ)& -\frac {100+\mathrm {j}100}{2-\mathrm {j}} &(カ)& \frac {{\dot Y}_{m}{\dot V}_{m}}{2} &(ヨ)& \frac {{\dot Y}_{1}+{\dot Y}_{2}+{\dot Y}_{3}}{{\dot Y}_{1}{\dot V}_{1}+{\dot Y}_{2}{\dot V}_{2}+{\dot Y}_{3}{\dot V}_{3}} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
不平衡三相交流回路の計算問題です。
電圧源と電流源の等価変換もミルマンの定理も\( \ 3 \ \)種の頃から扱っている内容となります。
\( \ 1 \ \)種の問題であるからと身構えず,基本公式を思い出し解くようにして下さい。
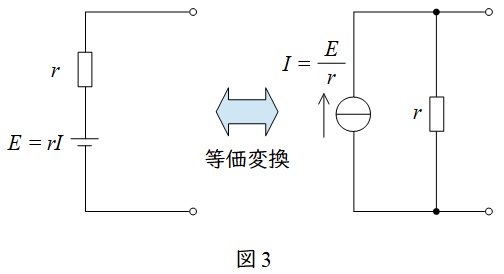
1.電圧源と電流源の等価変換
図3に示すように,電圧源と電流源は抵抗との直列接続と並列接続で等価変換をすることができます。
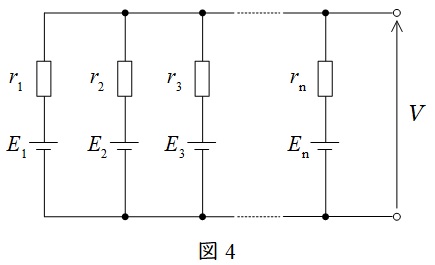
2.ミルマンの定理
図4のような,電源\( \ E_{1},E_{2},\cdots ,E_{\mathrm {n}} \ \)と抵抗\( \ r_{1},r_{2},\cdots ,r_{\mathrm {n}} \ \)が直並列された回路における全体の電圧\( \ V \ \)は,
\[
\begin{eqnarray}
V&=&\frac {\displaystyle \frac {E_{1}}{r_{1}}+\frac {E_{2}}{r_{2}}+\frac {E_{3}}{r_{3}}+\cdots +\frac {E_{\mathrm {n}}}{r_{\mathrm {n}}}}{\displaystyle \frac {1}{r_{1}}+\frac {1}{r_{2}}+\frac {1}{r_{3}}+\cdots +\frac {1}{r_{\mathrm {n}}}} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
【解答】
(1)解答:ロ
ワンポイント解説「1.電圧源と電流源の等価変換」の通り,\( \ {\dot V}_{1} \ \)と\( \ {\dot Z}_{1} \ \)を電流源に等価変換すると,
\[
\begin{eqnarray}
{\dot J}_{1}&=&\frac {{\dot V}_{1}}{{\dot Z}_{1}} \\[ 5pt ]
&=&{\dot Y}_{1}{\dot V}_{1} \\[ 5pt ]
\end{eqnarray}
\]
となり,他の二相も同様にして求められるため,\( \ {\dot J}_{m}={\dot Y}_{m}{\dot V}_{m} \ \)と求められる。
(2)解答:ハ
\( \ {\dot V}_{1} \ \)と\( \ {\dot Z}_{1} \ \)及び\( \ {\dot V}_{4} \ \)にキルヒホッフの法則を適用すれば,
\[
\begin{eqnarray}
{\dot V}_{1}-{\dot V}_{4}&=&{\dot Z}_{1}{\dot I}_{1} \\[ 5pt ]
{\dot I}_{1}&=&\frac {{\dot V}_{1}-{\dot V}_{4}}{{\dot Z}_{1}} \\[ 5pt ]
&=&\left( {\dot V}_{1}-{\dot V}_{4}\right) {\dot Y}_{1} \\[ 5pt ]
\end{eqnarray}
\]
となり,他の二相も同様にして求められるため,\( \ {\dot I}_{m}=\left( {\dot V}_{m}-{\dot V}_{4}\right) {\dot Y}_{m} \ \)と求められる。
(3)解答:ト
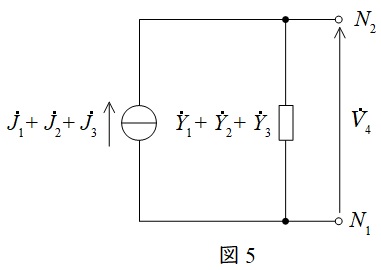
図2の回路を一つの電流源とアドミタンスに合成すると,図5のようになるため,
\[
\begin{eqnarray}
{\dot V}_{4}&=&\frac {{\dot J}_{1}+{\dot J}_{2}+{\dot J}_{3}}{{\dot Y}_{1}+{\dot Y}_{2}+{\dot Y}_{3}} \\[ 5pt ]
&=&\frac {{\dot Y}_{1}{\dot V}_{1}+{\dot Y}_{2}{\dot V}_{2}+{\dot Y}_{3}{\dot V}_{3}}{{\dot Y}_{1}+{\dot Y}_{2}+{\dot Y}_{3}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ワ
(5)解答:ヘ
三相負荷の各アドミタンスは,
\[
\begin{eqnarray}
{\dot Y}_{1}&=&\frac {1}{{\dot Z}_{1}} \\[ 5pt ]
&=&\frac {1}{\mathrm {j}} \\[ 5pt ]
&=&\frac {1}{\mathrm {j}}\times \frac {\mathrm {j}}{\mathrm {j}} \\[ 5pt ]
&=&-\mathrm {j} \ \mathrm {[S]} \\[ 5pt ]
{\dot Y}_{2}&=&{\dot Y}_{3}=1 \ \mathrm {[S]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,それぞれ(3)解答式に代入すると,
\[
\begin{eqnarray}
{\dot V}_{4}&=&\frac {{\dot Y}_{1}{\dot V}_{1}+{\dot Y}_{2}{\dot V}_{2}+{\dot Y}_{3}{\dot V}_{3}}{{\dot Y}_{1}+{\dot Y}_{2}+{\dot Y}_{3}} \\[ 5pt ]
&=&\frac {-\mathrm {j}{\dot V}_{1}+1\times {\dot V}_{2}+1\times {\dot V}_{3}}{-\mathrm {j}+1+1} \\[ 5pt ]
&=&\frac {-\mathrm {j}{\dot V}_{1}+{\dot V}_{2}+{\dot V}_{3}}{2-\mathrm {j}} \\[ 5pt ]
\end{eqnarray}
\]
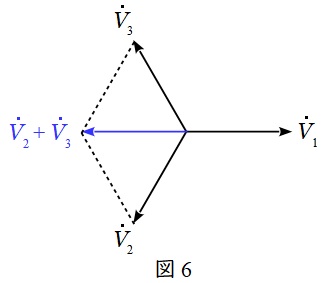
となり,図6に示す通り,\( \ {\dot V}_{2}+{\dot V}_{3}=-{\dot V}_{1} \ \)((5)解答)であるから,
\[
\begin{eqnarray}
{\dot V}_{4}&=&\frac {-\mathrm {j}{\dot V}_{1}+{\dot V}_{2}+{\dot V}_{3}}{2-\mathrm {j}} \\[ 5pt ]
&=&\frac {-\mathrm {j}{\dot V}_{1}-{\dot V}_{1}}{2-\mathrm {j}} \\[ 5pt ]
&=&\frac {-\mathrm {j}100-100}{2-\mathrm {j}} \\[ 5pt ]
&=&-\frac {100+\mathrm {j}100}{2-\mathrm {j}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん