【問題】
【難易度】★★☆☆☆(やや易しい)
次の文章は,直線電荷が作り出す電界に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
真空中に線電荷密度\( \ +\lambda \left( \lambda > 0 \right) \ \)の無限長直線電荷\( \ 1 \ \)本が距離\( \ r \ \)離れた点に作る電界の大きさ\( \ E \left( r\right) \ \)は\( \ \fbox { (1) } \ \)と求められる。ただし,真空中の誘電率を\( \ \varepsilon _{0} \ \)とする。
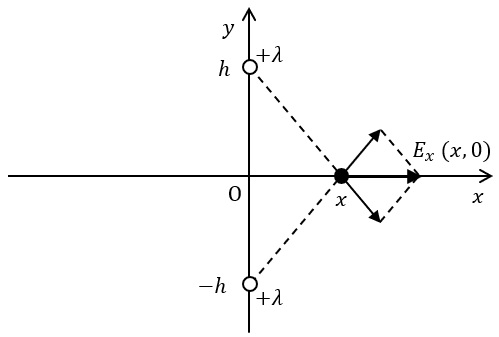
次に,真空中の\( \ xyz \ \)座標空間上に線電荷密度\( \ +\lambda \ \)の無限長直線電荷\( \ 2 \ \)本を置く。それらはともに\( \ z \ \)軸に平行で,\( \ x=0 \ \),\( \ y=±h \ \)の位置にある。図は\( \ xy \ \)平面上での断面を表し,以降は\( \ xy \ \)平面で考える。
ここで,\( \ x \ \)軸上の電界を考える。図のように二つの線電荷が\( \ x \ \)軸上に作る電界の\( \ x \ \)成分\( \ E_{x} \left( x , 0 \right) \ \)は\( \ \fbox { (2) } \ \)となる。\( \ E_{x} \left( x , 0 \right) \ \)が最大となるのは\( \ x= \ \fbox { (3) } \ \)のときで,その最大値は\( \ \fbox { (4) } \ \)である。原点\( \ \mathrm {O} \ \)を電位の基準とするとき,点\( \ \left( x_{0} , 0 \right) \ \)における電位\( \ V \left( x_{0} , 0 \right) \ \)は\( \ \fbox { (5) } \ \)である。
〔問1の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {\lambda }{2\pi \varepsilon _{0}}\ln \frac {x_{0}h}{{x_{0}}^{2}+h^{2}} &(ロ)& \frac {\lambda }{4\pi \varepsilon _{0}r^{2}} &(ハ)& \frac {\lambda }{\pi \varepsilon _{0}}\frac {hx}{\left( {x_{0}}^{2}+h^{2}\right) ^{\frac {3}{2}}} \\[ 5pt ]
&(ニ)& \frac {\lambda }{\pi \varepsilon _{0}} \frac {x}{x^{2}+h^{2}} &(ホ)& \frac {\lambda }{2\pi \varepsilon _{0}r} &(ヘ)& \frac {h}{\sqrt {3}} \\[ 5pt ]
&(ト)& \frac {\lambda }{6\pi \varepsilon _{0}h} &(チ)& \frac {\lambda }{2\pi \varepsilon _{0}}\ln \frac {h^{2}}{{x_{0}}^{2}+h^{2}} &(リ)& \frac {\lambda }{\pi \varepsilon _{0}} \frac {h}{x^{2}+h^{2}} \\[ 5pt ]
&(ヌ)& \frac {\lambda }{2\pi \varepsilon _{0}h} &(ル)& h &(ヲ)& \frac {\lambda }{3\pi \varepsilon _{0}r^{3}} \\[ 5pt ]
&(ワ)& \sqrt {3}h &(カ)& \frac {3\lambda }{2\pi \varepsilon _{0}h} &(ヨ)& \frac {\lambda }{2\pi \varepsilon _{0}}\ln \frac {{x_{0}}^{2}}{{x_{0}}^{2}+h^{2}} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
直線電荷が作る電界に関する問題です。
(5)で数学力が求められますが,電界や電位の考え方としての難易度は高くないため,完答を目指したい問題です。
\( \ 2 \ \)種以上になると線電荷の出題も増えるので,点電荷と勘違いしてしまう受験生は少ないと思いますが,勘違いしてしまうと全て誤答となってしまうので十分注意して下さい。
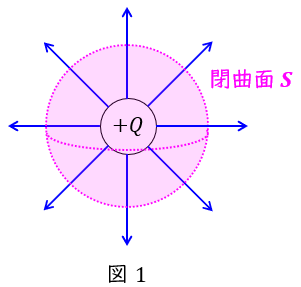
1.ガウスの法則
\( \ Q \ \mathrm {[C]} \ \)から出る電気力線は\( \ \displaystyle \frac {Q}{\varepsilon } \ \)本,電束は\( \ Q \ \)本であり,電界\( \ E \ \mathrm {[V / m]} \ \)及び電束密度\( \ D \ \mathrm {[C / m^{2}]} \ \)との関係は,任意の閉曲面において,
\[
\begin{eqnarray}
\int _{S} \boldsymbol E \cdot \mathrm {d}\boldsymbol S &=& \frac {Q}{\varepsilon } \\[ 5pt ]
\int _{S} \boldsymbol D \cdot \mathrm {d}\boldsymbol S &=& Q \\[ 5pt ]
\end{eqnarray}
\]
となり,これをガウスの法則といいます。閉曲面が球で,点電荷に蓄えられている電荷\( \ Q \ \mathrm {[C]} \ \)があれば,電界\( \ E \ \mathrm {[V / m]} \ \)は,
\[
\begin{eqnarray}
4\pi r^{2} \cdot E &=& \frac {Q}{\varepsilon } \\[ 5pt ]
E &=& \frac {Q}{4\pi \varepsilon r^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
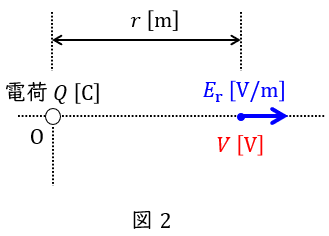
2.空間上の電位\( \ V \ \)
中心からの距離\( \ r \ \mathrm {[m]} \ \)に関する電界\( \ E_{\mathrm {r}} \ \mathrm {[V / m]} \ \)が与えられている時,その場所の電位\( \ V \ \mathrm {[V]} \ \)は無限遠を基準とすると,
\[
\begin{eqnarray}
V&=&-\int _{\infty }^{r}E_{\mathrm {r}}\mathrm {d}r \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
3.積と商の微分公式(数学)
\( \ x \ \)の関数\( \ u\left( x \right) \ \)及び\( \ v\left( x \right) \ \)があり,それぞれの微分が\( \ u^{\prime }\left( x \right) \ \)及び\( \ v^{\prime }\left( x \right) \ \)であるとき,それぞれの積と商の微分は,
\[
\begin{eqnarray}
\left\{ u\left( x \right) v\left( x \right) \right\} ^{\prime }&=&u^{\prime }\left( x \right) v\left( x \right) +u\left( x \right) v^{\prime }\left( x \right) \\[ 5pt ]
\left\{ \frac {u\left( x \right) }{v\left( x \right) }\right\} ^{\prime }&=&\frac {u^{\prime }\left( x \right) v\left( x \right) -u\left( x \right) v^{\prime }\left( x \right) }{v\left( x \right) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)解答:ホ
線電荷密度\( \ +\lambda \left( \lambda > 0 \right) \ \)の無限長直線電荷\( \ 1 \ \)本が距離\( \ r \ \)離れた点に作る電界の大きさ\( \ E \left( r\right) \ \)は,ワンポイント解説「1.ガウスの法則」の通り,
\[
\begin{eqnarray}
2\pi r E \left( r\right) &=& \frac {\lambda }{\varepsilon _{0}} \\[ 5pt ]
E \left( r\right) &=& \frac {\lambda }{2\pi \varepsilon _{0}r} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ニ
線電荷と点\( \ \left( x , 0 \right) \ \)の距離\( \ r \ \)は,
\[
\begin{eqnarray}
r &=& \sqrt {x^{2}+h^{2}} \\[ 5pt ]
\end{eqnarray}
\]
であるため,一つの線電荷が点\( \ \left( x , 0 \right) \ \)に作る電界の大きさ\( \ E_{1} \left( x , 0 \right) \ \)は,
\[
\begin{eqnarray}
E_{1} \left( x , 0 \right) &=& \frac {\lambda }{2\pi \varepsilon _{0}r} \\[ 5pt ]
&=& \frac {\lambda }{2\pi \varepsilon _{0}\sqrt {x^{2}+h^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,\( \ E_{1} \left( x , 0 \right) \ \)の\( \ x \ \)成分\( \ E_{1x} \left( x , 0 \right) \ \)は,
\[
\begin{eqnarray}
E_{1x} \left( x , 0 \right) &=& E_{1} \left( x , 0 \right) \cdot \frac {x}{r} \\[ 5pt ]
&=& \frac {\lambda }{2\pi \varepsilon _{0}\sqrt {x^{2}+h^{2}}} \frac {x}{\sqrt {x^{2}+h^{2}}} \\[ 5pt ]
&=& \frac {\lambda }{2\pi \varepsilon _{0}} \frac {x}{x^{2}+h^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となり,もう一方の線電荷が点\( \ \left( x , 0 \right) \ \)に作る電界の\( \ x \ \)成分も同じ大きさなので,二つの線電荷が点\( \ \left( x , 0 \right) \ \)に作る電界の大きさの\( \ x \ \)成分\( \ E_{x} \left( x , 0 \right) \ \)は,
\[
\begin{eqnarray}
E_{x} \left( x , 0 \right) &=& 2E_{1x} \left( x , 0 \right) \\[ 5pt ]
&=& \frac {\lambda }{\pi \varepsilon _{0}} \frac {x}{x^{2}+h^{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ル
(2)で求めた\( \ E_{x} \left( x , 0 \right) \ \)の両辺を\( \ x \ \)で微分すると,ワンポイント解説「3.積と商の微分公式(数学)」の通り,
\[
\begin{eqnarray}
\frac {\mathrm {d}E_{x} \left( x , 0 \right) }{\mathrm {d}x} &=& \frac {\lambda }{\pi \varepsilon _{0}} \frac {1\cdot \left( x^{2}+h^{2}\right) -x\cdot 2x }{\left( x^{2}+h^{2}\right) ^{2}} \\[ 5pt ]
&=& \frac {\lambda }{\pi \varepsilon _{0}} \frac {h^{2}-x^{2} }{\left( x^{2}+h^{2}\right) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ \displaystyle \frac {\mathrm {d}E_{x} \left( x , 0 \right) }{\mathrm {d}x}=0 \ \)のとき\( \ E_{x} \left( x , 0 \right) \ \)は最大となるから,
\[
\begin{eqnarray}
\frac {\lambda }{\pi \varepsilon _{0}} \frac {h^{2}-x^{2} }{\left( x^{2}+h^{2}\right) ^{2}} &=&0 \\[ 5pt ]
h^{2}-x^{2} &=& 0 \\[ 5pt ]
x^{2} &=& h^{2} \\[ 5pt ]
x &=& h \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ヌ
(2)解答式に(3)解答式を代入すると,\( \ E_{x} \left( x , 0 \right) \ \)の最大値\( \ E_{x\mathrm {m}} \left( x , 0 \right) \ \)
\[
\begin{eqnarray}
E_{x\mathrm {m}} \left( x , 0 \right) &=& \frac {\lambda }{\pi \varepsilon _{0}} \frac {h}{h^{2}+h^{2}} \\[ 5pt ]
&=& \frac {\lambda }{2\pi \varepsilon _{0}h} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:チ
(2)解答式より,原点\( \ \mathrm {O} \ \)を電位の基準とするときの点\( \ \left( x_{0} , 0 \right) \ \)における電位\( \ V \left( x_{0} , 0 \right) \ \)は,ワンポイント解説「2.空間上の電位\( \ V \ \)」の通り,
\[
\begin{eqnarray}
V \left( x_{0} , 0 \right)&=&-\int _{0 }^{x_{0}}E_{x} \left( x , 0 \right) \mathrm {d}x \\[ 5pt ]
&=&-\int _{0 }^{x_{0}} \frac {\lambda }{\pi \varepsilon _{0}} \frac {x}{x^{2}+h^{2}} \mathrm {d}x \\[ 5pt ]
&=&-\frac {\lambda }{\pi \varepsilon _{0}}\int _{0 }^{x_{0}} \frac {x}{x^{2}+h^{2}} \mathrm {d}x \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ A=x^{2}+h^{2} \ \)とおけば,\( \ \displaystyle \frac {\mathrm {d}A}{\mathrm {d}x}=2x ⇔ \mathrm {d}x =\frac {\mathrm {d}A}{2x} \ \)であり,\( \ x=0 \ \)のとき\( \ A=h^{2} \ \),\( \ x=x_{0} \ \)のとき\( \ A={x_{0}}^{2}+h^{2} \ \)となるので,
\[
\begin{eqnarray}
V \left( x_{0} , 0 \right) &=&-\frac {\lambda }{\pi \varepsilon _{0}}\int _{h^{2}}^{{x_{0}}^{2}+h^{2}} \frac {x}{A} \frac {\mathrm {d}A}{2x} \\[ 5pt ]
&=&-\frac {\lambda }{2\pi \varepsilon _{0}}\int _{h^{2}}^{{x_{0}}^{2}+h^{2}} \frac {1}{A} \mathrm {d}A \\[ 5pt ]
&=&-\frac {\lambda }{2\pi \varepsilon _{0}}\left[ \ln A \right] _{h^{2}}^{{x_{0}}^{2}+h^{2}} \\[ 5pt ]
&=&-\frac {\lambda }{2\pi \varepsilon _{0}}\left\{ \ln \left( {x_{0}}^{2}+h^{2}\right) – \ln h^{2} \right\} \\[ 5pt ]
&=&\frac {\lambda }{2\pi \varepsilon _{0}}\left\{ \ln h^{2} -\ln \left( {x_{0}}^{2}+h^{2}\right) \right\} \\[ 5pt ]
&=&\frac {\lambda }{2\pi \varepsilon _{0}}\ln \frac {h^{2}}{{x_{0}}^{2}+h^{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん