《理論》〈電子理論〉[R07:問3]時分割形乗算器の動作原理に関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，時分割形乗算器の動作原理に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

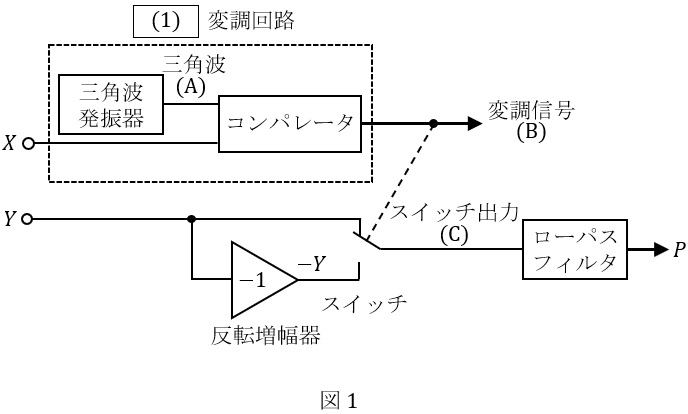
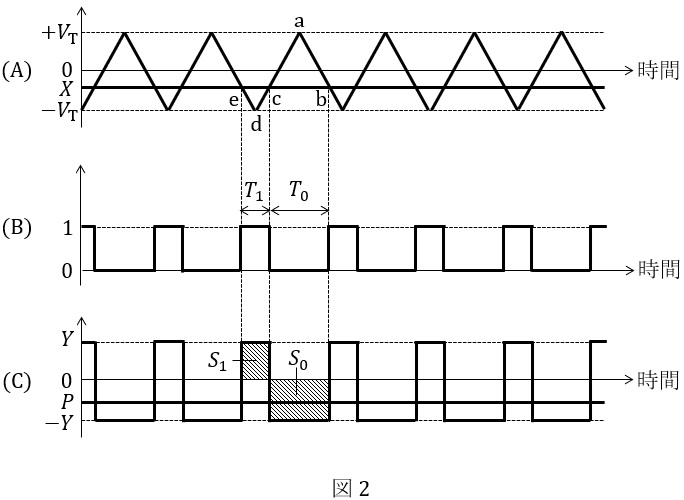
図1に示す回路は，直流電圧の$ \ X \ $及び$ \ Y \ $の積に比例した電圧$ \ P \ $を出力する時分割形乗算器である。また，図2は回路内の各信号波形を表す。

図1の破線枠内の回路は，一般に$ \ \fbox {　（１）　} \ $変調回路と呼ばれる。$ \ \fbox {　（１）　} \ $変調回路では，三角波発振器から図2$ \ \mathrm {(A)} \ $に示す振幅が$ \ ±V_{\mathrm {T}} \ $である三角波を出力し，コンパレータは，$ \ X \ $と三角波の大小関係に応じて，図2$ \ \mathrm {(B)} \ $に示す論理値$ \ 0 \ $又は$ \ 1 \ $の変調信号を出力する。ただし，$ \ -V_{\mathrm {T}} ＜ X ＜ +V_{\mathrm {T}} \ $とする。

ここで，図2$ \ \mathrm {(A)} \ $の$ \ \mathrm {△abc} \ $と$ \ \mathrm {△dec} \ $が相似であることを利用すれば，$ \ \displaystyle \frac {T_{1}}{T_{0}}= \ \fbox {　（２）　} \ $となる。これを$ \ X \ $について解けば，$ \ X= \ \fbox {　（３）　} \ $が得られる。

スイッチは変調信号に応じて接点が切り替わり，その出力波形は図2$ \ \mathrm {(C)} \ $に示す矩形波で表される。ここで，ローパスフィルタが直流のみを通過させる特性であるなら，$ \ P \ $はスイッチ出力の平均電圧になる。そこで，面積$ \ S_{0} \ $と面積$ \ S_{1} \ $に注目すれば，$ \ Y \ $，$ \ T_{0} \ $及び$ \ T_{1} \ $を用いて，$ \ P=\fbox {　（４）　} \ $が得られる。

さらに，$ \ \fbox {　（３）　} \ $及び$ \ \fbox {　（４）　} \ $から$ \ T_{0} \ $及び$ \ T_{1} \ $を消去すれば，$ \ P= \ \fbox {　（５）　} \ XY \ $となるから，本回路は積$ \ XY \ $に比例する$ \ P \ $を出力する乗算器であることが分かる。

〔問3の解答群〕
\[
\begin{eqnarray}
&（イ）&　\left( T_{1}+T_{0}\right) \left( T_{1}-T_{0}\right) V_{\mathrm {T}}　　　　　&（ロ）&　\frac {1}{V_{\mathrm {T}}}　　　　　&（ハ）&　\frac {V_{\mathrm {T}}+X}{V_{\mathrm {T}}-X} \\[ 5pt ] &（ニ）&　\frac {V_{\mathrm {T}}-X}{V_{\mathrm {T}}+X}　　　　　&（ホ）&　\left( V_{\mathrm {T}}+X\right) \left( V_{\mathrm {T}}-X\right) 　　　　　&（ヘ）&　振幅 \\[ 5pt ] &（ト）&　V_{\mathrm {T}}　　　　　&（チ）&　周波数　　　　　　　&（リ）&　\frac {T_{1}-T_{0}}{T_{1}+T_{0}}V_{\mathrm {T}} \\[ 5pt ] &（ヌ）&　\frac {T_{1}+T_{0}}{T_{1}-T_{0}}V_{\mathrm {T}}　　　　　&（ル）&　\frac {T_{1}-T_{0}}{T_{1}+T_{0}}Y　　　　　&（ヲ）&　\left( T_{1}+T_{0}\right) \left( T_{1}-T_{0}\right) Y \\[ 5pt ] &（ワ）&　2V_{\mathrm {T}}　　　　　&（カ）&　パルス幅　　　　　&（ヨ）&　\frac {T_{1}+T_{0}}{T_{1}-T_{0}}Y \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

時分割形乗算器に関する問題です。
理論科目というよりは機械科目のパワーエレクトロニクスのような問題で，問題文を読みながら考えていく必要がある問題です。
$ \ 1 \ $種では受験生にその場で考えさせる問題も出題されやすいので，しっかりと読破して解いていくようにして下さい。

【解答】

(1)解答：カ
題意より解答候補は，（ヘ）振幅，（チ）周波数，（カ）パルス幅，になると思います。
図2$ \ \mathrm {(B)} \ $の波形より，入力$ \ X \ $によりパルス幅が変化するパルス幅変調回路であることがわかります。

(2)解答：ハ
$ \ \mathrm {△abc} \ $と$ \ \mathrm {△dec} \ $が相似であるから，
\[
\begin{eqnarray}
\frac {T_{1}}{T_{0}} &=& \frac {X-\left( -V_{\mathrm {T}}\right) }{V_{\mathrm {T}}-X} \\[ 5pt ] &=& \frac {X+V_{\mathrm {T}} }{V_{\mathrm {T}}-X} \\[ 5pt ] &=& \frac {V_{\mathrm {T}}+X}{V_{\mathrm {T}}-X} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：リ
(2)解答式より，
\[
\begin{eqnarray}
\frac {T_{1}}{T_{0}} &=& \frac {V_{\mathrm {T}}+X}{V_{\mathrm {T}}-X} \\[ 5pt ] T_{1}\left( V_{\mathrm {T}}-X\right) &=&T_{0}\left( V_{\mathrm {T}}+X\right) \\[ 5pt ] V_{\mathrm {T}}T_{1}-XT_{1}&=&V_{\mathrm {T}}T_{0}+XT_{0} \\[ 5pt ] XT_{1}+XT_{0}&=&V_{\mathrm {T}}T_{1}-V_{\mathrm {T}}T_{0} \\[ 5pt ] X\left( T_{1}+T_{0}\right) &=&V_{\mathrm {T}}\left( T_{1}-T_{0}\right) \\[ 5pt ] X&=&\frac {T_{1}-T_{0}}{T_{1}+T_{0}}V_{\mathrm {T}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ル
面積$ \ S_{0} \ $と面積$ \ S_{1} \ $に注目し，平均値$ \ P \ $を求めると，
\[
\begin{eqnarray}
P &=& \frac {S_{1}-S_{0}}{T_{1}+T_{0}} \\[ 5pt ] &=& \frac {YT_{1}-YT_{0}}{T_{1}+T_{0}} \\[ 5pt ] &=& \frac {T_{1}-T_{0}}{T_{1}+T_{0}}Y \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ロ
(3)及び(4)より，
\[
\begin{eqnarray}
\frac {T_{1}-T_{0}}{T_{1}+T_{0}}=\frac {X}{V_{\mathrm {T}}} &=& \frac {P}{Y} \\[ 5pt ] P &=&\frac {1}{V_{\mathrm {T}}}XY \\[ 5pt ] \end{eqnarray}
\] と求められる。