【問題】
【難易度】★★★☆☆(普通)
次の文章は,回路の過渡現象に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
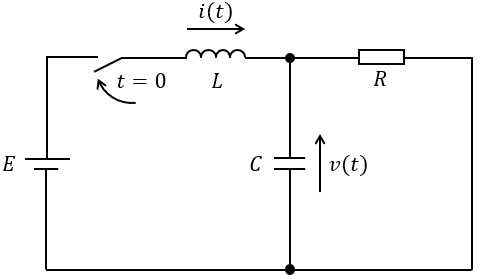
図に示す直流電圧源\( \ E \ \),インダクタンス\( \ L \ \)のコイル,静電容量\( \ C \ \)のコンデンサ,抵抗値\( \ R \ \)の抵抗,スイッチからなる回路を考える。時刻\( \ t < 0 \ \)でスイッチは開いており,コイルの磁束とコンデンサの電荷は零とする。\( \ t = 0 \ \)でスイッチを閉じた。
\( \ t ≧0 \ \)でのコイルの電流を\( \ i(t) \ \),コンデンサの電圧を\( \ v(t) \ \)とすると,回路図より\( \ i(t) \ \)と\( \ v(t) \ \)との間には次の関係式が成立する。
\[
\begin{eqnarray}
L\frac {\mathrm {d}}{\mathrm {d}t} i(t) &=& \ \fbox { (1) } \ ・・・・・・・・・・・・・・・・・・ ① \\[ 5pt ]
C\frac {\mathrm {d}}{\mathrm {d}t} v(t) &=& \ \fbox { (2) } \ ・・・・・・・・・・・・・・・・・・ ② \\[ 5pt ]
\end{eqnarray}
\]
回路の初期条件と②式から\( \ t=0 \ \)では\( \ \displaystyle \left. \frac {\mathrm {d}}{\mathrm {d}t} v(t)\right| _{t=0} = \ \fbox { (3) } \ \)である。
②式を微分した式に①式を代入すると\( \ v(t) \ \)の二階の微分方程式が得られる。\( \ v(t) \ \)の過渡解が減衰振動となるのは,その特性多項式の根が共役複素根となるときであり,条件\( \ \fbox { (4) } \ \)が成立するときである。
次に,\( \ t > 0 \ \)で\( \ v(t) \ \)が満たす不等式を導く。ここでは,詳細な導出は省略するが,①式と②式を利用して回路のエネルギー収支の式
\[
\begin{eqnarray}
\int _{0}^{t}Ei( \tau )\mathrm {d}\tau &=& \frac {1}{2}L\left[ i(t)\right] ^{2}+\frac {1}{2}C\left[ v(t)\right] ^{2}+\frac {1}{R}\int _{0}^{t}\left[ v(t)\right] ^{2}\mathrm {d}\tau \\[ 5pt ]
\end{eqnarray}
\]
を変形してゆくと,以下の式が得られる。
\[
\begin{eqnarray}
C\left\{ Ev(t)-\frac {1}{2}\left[ v(t)\right] ^{2} \right\} &=& \frac {1}{2}C^{2}L\left[ \frac {\mathrm {d}}{\mathrm {d}t} v(t)\right] ^{2} +\frac {CL}{R}\int _{0}^{t}\left[ \frac {\mathrm {d}}{\mathrm {d}\tau }v(\tau )\right] ^{2}\mathrm {d}\tau ・・・・ ③ \\[ 5pt ]
\end{eqnarray}
\]
③式の右辺の符号に注意すると,左辺のコンデンサの電圧\( \ v(t) \ \)は\( \ t > 0 \ \)で不等式\( \ \fbox { (5) } \ \)を満たすことが分かる。
〔問4の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {1}{R^{2}}-\frac {4C}{L}>0 &(ロ)& E+v(t) &(ハ)& i(t)-\frac {2v(t)}{R} \\[ 5pt ]
&(ニ)& 0<v(t)<2E &(ホ)& 0 &(ヘ)& \frac {E}{CR} \\[ 5pt ]
&(ト)& i(t)-\frac {v(t)}{R} &(チ)& -\frac {E}{CR} &(リ)& E-v(t) \\[ 5pt ]
&(ヌ)& 0<v(t)<\frac {1}{2}E &(ル)& i(t)+\frac {v(t)}{R} &(ヲ)& -E<v(t)<E \\[ 5pt ]
&(ワ)& \frac {1}{R^{2}}-\frac {4C}{L}<0 &(カ)& \frac {1}{R^{2}}-\frac {4C}{L}=0 &(ヨ)& 2E-v(t) \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
\( \ RLC \ \)直並列回路の過渡現象に関する問題です。
過渡現象といってもあまりストレートな問題ではなく,少し捻った出題をしている\( \ 1 \ \)種らしい問題です。
焦ると訳が分からなくなってしまうので,落ち着いて問題文をよく読みながら解いていくようにして下さい。
1.過渡現象における\( \ RLC \ \)それぞれの電圧
線路に流れる電流を\( \ i \ \mathrm {[A]} \ \)とし,抵抗\( \ R \ \mathrm {[\Omega ]} \ \)の電圧\( \ V_{\mathrm{R}} \ \mathrm {[V]} \ \),リアクトル\( \ L \ \mathrm {[H]} \ \)の電圧\( \ V_{\mathrm{L}} \ \mathrm {[V]} \ \),コンデンサ\( \ C \ \mathrm {[F]} \ \)の電圧\( \ V_{\mathrm{C}} \ \mathrm {[V]} \ \)とすると,
\[
\begin{eqnarray}
V_{\mathrm{R}} &=& Ri \\[ 5pt ]
V_{\mathrm{L}} &=& L\frac {\mathrm {d}i}{\mathrm {d}t} \\[ 5pt ]
V_{\mathrm{C}} &=& \frac {1}{C}\int i \mathrm {d}t =\frac {q}{C}\\[ 5pt ]
\end{eqnarray}
\]
となります。
2.過渡現象における定常解と過渡解
ⅰ.定常解を\( \ i_{\mathrm {s}} \ \),過渡解を\( \ i_{\mathrm {t}} \ \)とすると,電流値\( \ i \ \)は\( \ i=i_{\mathrm {s}}+i_{\mathrm {t}} \ \)となります。
ⅱ.定常解は電流の時間変化のない状態すなわち\( \ \displaystyle \frac {\mathrm {d}i_{\mathrm {s}}}{\mathrm {d}t}=0 \ \)とした時の解です。
ⅲ.過渡解はスイッチを入れた直後の解です。
3.自然対数の微分積分
①自然対数の微分
\[
\begin{eqnarray}
\frac {\mathrm {d}}{\mathrm {d}x} \left ( \ln {x} \right) &=&\frac {1}{x} \\[ 5pt ]
\end{eqnarray}
\]
②自然対数の積分
\[
\begin{eqnarray}
\int \frac {1}{x} \mathrm {d}x&=&\ln {x} + C \left( Cは積分定数\right) \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
\ln {x} &=&-\alpha t +C \left( Cは積分定数\right)の時, x=A\mathrm {e}^{-\alpha t} \left( A=\mathrm {e}^{C}\right)となります。 \\[ 5pt ]
\end{eqnarray}
\]
4.特性方程式
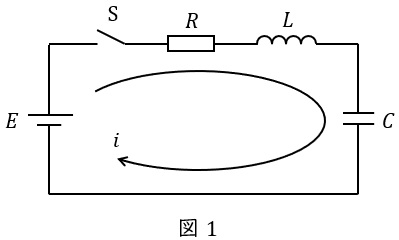
図1のような\( \ RLC \ \)回路があるとき,回路方程式は,
\[
\begin{eqnarray}
L\frac {\mathrm {d}i}{\mathrm {d}t}+Ri+\frac {1}{C}\int i \mathrm {d}t&=&E \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ \displaystyle i=\frac {\mathrm {d}q}{\mathrm {d}t} \ \)の関係があるから,
\[
\begin{eqnarray}
L\frac {\mathrm {d}^{2}q}{\mathrm {d}t^{2}}+R\frac {\mathrm {d}q}{\mathrm {d}t}+\frac {q}{C}&=&E \\[ 5pt ]
\end{eqnarray}
\]
となります。ここで,過渡解\( \ \left( E=0 \right) \ \)を求めるために\( \ \displaystyle q=A\mathrm {e}^{\alpha t} \ \) ( \( \ A \ \),\( \ \alpha \ \)は定数 )とおくと,
\[
\begin{eqnarray}
\frac {\mathrm {d}q}{\mathrm {d}t} &=& \alpha A\mathrm {e}^{\alpha t}\\[ 5pt ]
\frac {\mathrm {d}^{2}q}{\mathrm {d}t^{2}} &=& \alpha ^{2}A\mathrm {e}^{\alpha t} \\[ 5pt ]
\end{eqnarray}
\]
となるので,これを回路方程式に代入すると,
\[
\begin{eqnarray}
L\alpha ^{2}A\mathrm {e}^{\alpha t}+R\alpha A\mathrm {e}^{\alpha t}+\frac {1}{C}A\mathrm {e}^{\alpha t}&=&0 \\[ 5pt ]
L\alpha ^{2}+R\alpha +\frac {1}{C}&=&0 \\[ 5pt ]
\alpha ^{2}+\frac {R}{L}\alpha +\frac {1}{LC}&=&0 \\[ 5pt ]
\end{eqnarray}
\]
となり,これを特性方程式といいます。
【解答】
(1)解答:リ
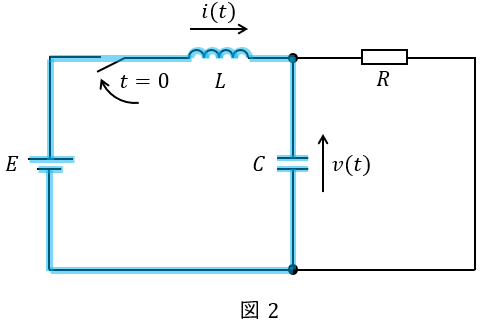
図2に示す閉回路の回路方程式より,
\[
\begin{eqnarray}
L\frac {\mathrm {d}}{\mathrm {d}t} i(t)+v(t) &=& E \\[ 5pt ]
L\frac {\mathrm {d}}{\mathrm {d}t} i(t) &=& E-v(t) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ト
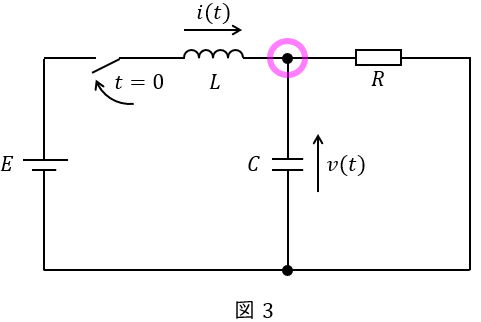
図3に示す節点にキルヒホッフの法則の電流則を適用すると,
\[
\begin{eqnarray}
i(t) &=& C\frac {\mathrm {d}}{\mathrm {d}t} v(t) +\frac {v(t)}{R} \\[ 5pt ]
C\frac {\mathrm {d}}{\mathrm {d}t} v(t) &=& i(t)-\frac {v(t)}{R} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ホ
初期条件より,\( \ i(0) =0 \ \)及び\( \ v(0) =0 \ \)であるから,(2)解答式より,
\[
\begin{eqnarray}
C\left. \frac {\mathrm {d}}{\mathrm {d}t} v(t) \right| _{t=0} &=& 0-\frac {0}{R} \\[ 5pt ]
\left. \frac {\mathrm {d}}{\mathrm {d}t} v(t) \right| _{t=0} &=& 0 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ワ
(2)解答式を\( \ t \ \)で微分すると,
\[
\begin{eqnarray}
C\frac {\mathrm {d}^{2}}{\mathrm {d}t^{2}} v(t) &=& \frac {\mathrm {d}}{\mathrm {d}t} i(t)-\frac {1}{R}\frac {\mathrm {d}}{\mathrm {d}t} v(t) \\[ 5pt ]
\frac {\mathrm {d}}{\mathrm {d}t} i(t) &=& C\frac {\mathrm {d}^{2}}{\mathrm {d}t^{2}} v(t) +\frac {1}{R}\frac {\mathrm {d}}{\mathrm {d}t} v(t) \\[ 5pt ]
\end{eqnarray}
\]
となり,これを(1)解答式を代入すると,
\[
\begin{eqnarray}
L\frac {\mathrm {d}}{\mathrm {d}t} i(t) &=& E-v(t) \\[ 5pt ]
L\left\{ C\frac {\mathrm {d}^{2}}{\mathrm {d}t^{2}} v(t) +\frac {1}{R}\frac {\mathrm {d}}{\mathrm {d}t} v(t) \right\} &=& E-v(t) \\[ 5pt ]
LC\frac {\mathrm {d}^{2}}{\mathrm {d}t^{2}} v(t) +\frac {L}{R}\frac {\mathrm {d}}{\mathrm {d}t} v(t) &=& E-v(t) \\[ 5pt ]
LC\frac {\mathrm {d}^{2}}{\mathrm {d}t^{2}} v(t) +\frac {L}{R}\frac {\mathrm {d}}{\mathrm {d}t} v(t) +v(t)&=& E \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,\( \ E=0 \ \)としたときの特性方程式は,ワンポイント解説「4.特性方程式」の通り,
\[
\begin{eqnarray}
LC\alpha ^{2} +\frac {L}{R}\alpha +1&=& 0 \\[ 5pt ]
\alpha ^{2} +\frac {1}{RC}\alpha +\frac {1}{LC}&=& 0 \\[ 5pt ]
\end{eqnarray}
\]
となるので,根を求めると,
\[
\begin{eqnarray}
\alpha &=& \frac {\displaystyle -\frac {1}{RC}±\sqrt {\left( \frac {1}{RC}\right) ^{2}-\frac {4}{LC}}}{2} \\[ 5pt ]
\end{eqnarray}
\]
となる。これより,共役複素根となる条件は,根号内が負となるときであるから,
\[
\begin{eqnarray}
\left( \frac {1}{RC}\right) ^{2}-\frac {4}{LC} &<& 0 \\[ 5pt ]
\frac {1}{R^{2}C^{2}}-\frac {4}{LC} &<& 0 \\[ 5pt ]
\frac {1}{R^{2}}-\frac {4C}{L}&<&0
\end{eqnarray}
\]
と求められる。
(5)解答:ニ
③式の右辺の各項はいずれも\( \ 2 \ \)乗の数と正の定数で構成されているため,いずれも正となる。したがって,
\[
\begin{eqnarray}
C\left\{ Ev(t)-\frac {1}{2}\left[ v(t)\right] ^{2} \right\} &>&0 \\[ 5pt ]
Ev(t)-\frac {1}{2}\left[ v(t)\right] ^{2} &>&0 \\[ 5pt ]
v(t)\left\{ E-\frac {1}{2}v(t)\right\} &>&0 \\[ 5pt ]
v(t)\left\{ 2E-v(t)\right\} &>&0 \\[ 5pt ]
v(t)\left\{ v(t)-2E\right\} &<&0 \\[ 5pt ]
0 &<&v(t)<2E \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん