《理論》〈電磁気〉[R04:問2]磁気回路のオームの法則に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，磁気回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。なお，真空の透磁率は\( \ \mu _{0} \ \)，鉄心の比透磁率は\( \ \mu _{\mathrm {r}} \ \)であり，鉄心の磁束の飽和やヒステリシス特性は無視できるものとする。

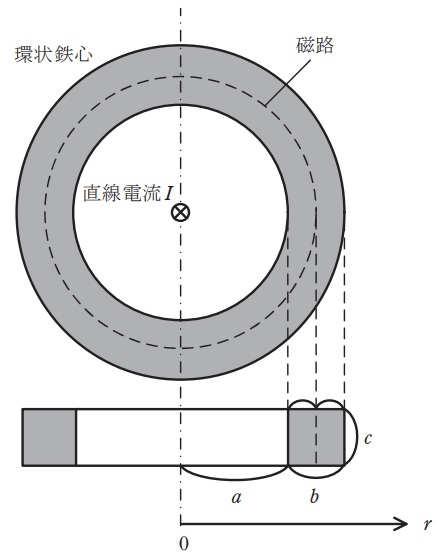
図に示すように，中央部の穴の半径が\( \ a \ \)，断面の形状が幅\( \ b \ \)，高さ\( \ c \ \)の長方形である環状鉄心があり，その中心軸上を直線電流\( \ I \ \)が流れている。アンペアの周回積分の法則を用いると，中心から距離\( \ r \ \)の鉄心内部の地点\( \ \left( a≦r≦a+b \right) \ \)の磁束密度の大きさは\( \ B\left( r \right) = \ \fbox {　 （１） 　} \ \)と求められるので，鉄心内の磁束は，
\[
\begin{eqnarray}
\mathit {\Phi }_{\mathrm {ampere}} &=& c \int _{a}^{a+b}B\left( r \right) \mathrm {d}r = \ \fbox {　 （２） 　} \\[ 5pt ] \end{eqnarray}
\] となる。

鉄心内部の磁束を簡便に取り扱う近似手法として，磁気回路が用いられる場合がある。鉄心の断面の中心を通る円周を磁路とすると，磁気抵抗は\( \ R_{\mathrm {m}}= \ \fbox {　 （３） 　} \ \)となるので，磁気回路に基づいて求めた鉄心内の磁束は，
\[
\begin{eqnarray}
\mathit {\Phi }_{\mathrm {mc}} &=& \frac {I}{R_{\mathrm {m}}} = \ \fbox {　 （４） 　} \\[ 5pt ] \end{eqnarray}
\] となる。

\( \ a=2 \ \mathrm {cm},b=1 \ \mathrm {cm},c=1 \ \mathrm {cm},\mu _{\mathrm {r}}=5 \ 000,I=1 \ \mathrm {kA} \ \)の場合を考えると，\( \ \mathit {\Phi }_{\mathrm {ampere}} \ \)と\( \ \mathit {\Phi }_{\mathrm {mc}} \ \)の値はともに\( \ \fbox {　 （５） 　} \ \mathrm {mWb} \ \)程度となるので，この条件では磁気回路による取り扱いがかなり正確であることがわかる。なお，真空の透磁率を\( \ \mu _{0}=4\pi \times 10^{-7} \ \mathrm {H / m} \ \)とし，必要であれば\( \ \ln 1.5 ≈ 0.4 \ \)を用いてもよい。

〔問2の解答群〕
\[
\begin{eqnarray}
&（イ）&　0.3　　　　　&（ロ）&　\frac {\mu _{0}\mu _{\mathrm {r}}Ibc}{2\pi a}　　　　　&（ハ）&　200 \\[ 5pt ] &（ニ）&　\frac {\pi }{\mu _{0}\mu _{\mathrm {r}}}\frac {a+b}{bc}　　　　　&（ホ）&　\frac {\mu _{0}\mu _{\mathrm {r}}Ic}{2\pi}\ln \frac {b}{a}　　　　　&（ヘ）&　\frac {\mu _{0}\mu _{\mathrm {r}}Ic}{\pi} \\[ 5pt ] &（ト）&　\frac {\mu _{0}\mu _{\mathrm {r}}Ic}{2\pi}\ln \frac {a+b}{a}　　　　　&（チ）&　\frac {I}{2\pi r}　　　　　&（リ）&　\frac {\mu _{0}\mu _{\mathrm {r}}I}{\pi}\frac {bc}{2a+b} \\[ 5pt ] &（ヌ）&　\frac {\mu _{0}\mu _{\mathrm {r}}I}{2\pi r}　　　　　&（ル）&　\frac {1}{\mu _{0}\mu _{\mathrm {r}}c}　　　　　&（ヲ）&　4 \\[ 5pt ] &（ワ）&　\frac {\mu _{0}I}{2\pi r}　　　　　&（カ）&　\frac {\pi }{\mu _{0}\mu _{\mathrm {r}}}\frac {2a+b}{bc}　　　　　&（ヨ）&　\frac {\mu _{0}\mu _{\mathrm {r}}I}{\pi}\frac {bc}{a+b} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

長方形の環状鉄心を用いた磁気回路に関する問題です。
(2)の考え方が本問の最重要ポイントですが，本問では式が与えられていますので，かなりの受験生が助けられたのではないかと思います。
基本的には(2)の積分の式は与えられない前提で解けるようにして下さい。

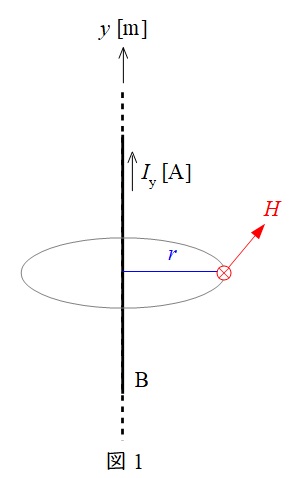
1.アンペールの周回積分の法則
図1のように無限長直線電流\( \ I_{\mathrm {y}} \ \)が流れているとき，電線から距離\( \ r \ \)の位置での磁界の強さ\( \ H \ \)は，
\[
\begin{eqnarray}
H&=&\frac {I_{\mathrm {y}}}{2\pi r} \\[ 5pt ] \end{eqnarray}
\] となります。

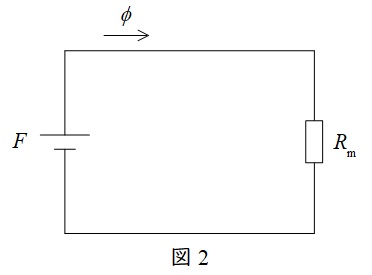
2.磁気回路のオームの法則
中心長さ\( \ l \ \)の環状鉄心に巻き数\( \ N \ \)のコイルが巻かれ，そこに電流\( \ I \ \)が流れている時，鉄心内の磁界の強さ\( \ H \ \)は，アンペールの周回積分の法則より，
\[
\begin{eqnarray}
NI&=&Hl \\[ 5pt ] H&=&\frac {NI}{l} \\[ 5pt ] \end{eqnarray}
\] であるから，鉄心内の磁束密度\( \ B \ \)は，鉄心内の透磁率\( \ \mu \ \)とすると，
\[
\begin{eqnarray}
B&=&\mu H \\[ 5pt ] &=&\frac {\mu NI}{l} \\[ 5pt ] \end{eqnarray}
\] となります。鉄心内の磁束\( \ \phi \ \)は，鉄心の断面積\( \ S \ \)とすると，
\[
\begin{eqnarray}
\phi &=&BS \\[ 5pt ] &=&\frac {\mu NIS}{l} \\[ 5pt ] &=&\frac {NI}{\displaystyle \frac {l}{\mu S}} \\[ 5pt ] \end{eqnarray}
\] となり，起磁力\( \ F=NI \ \)，磁気抵抗\( \ R_{\mathrm {m}}=\displaystyle \frac {l}{\mu S} \ \)とすると，
\[
\begin{eqnarray}
\phi &=&\frac {F}{R_{\mathrm {m}}} \\[ 5pt ] \end{eqnarray}
\] となり，磁気回路のオームの法則が成立します。

【解答】

(1)解答：ヌ
直線電流\( \ I \ \)が中心から距離\( \ r \ \)に作る磁界の大きさ\( \ H \ \)は，ワンポイント解説「1.アンペールの周回積分の法則」の通り，
\[
\begin{eqnarray}
H &=&\frac {I}{2\pi r} \\[ 5pt ] \end{eqnarray}
\] であるため，鉄心内部の地点\( \ \left( a≦r≦a+b \right) \ \)の磁束密度の大きさ\( \ B\left( r \right) \ \)は，
\[
\begin{eqnarray}
B\left( r \right) &=&\mu _{0}\mu _{\mathrm {r}}H \\[ 5pt ] &=&\mu _{0}\mu _{\mathrm {r}}\cdot \frac {I}{2\pi r} \\[ 5pt ] &=&\frac {\mu _{0}\mu _{\mathrm {r}}I}{2\pi r} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ト
題意より，鉄心内の磁束\( \ \mathit {\Phi }_{\mathrm {ampere}} \ \)は，
\[
\begin{eqnarray}
\mathit {\Phi }_{\mathrm {ampere}} &=& c \int _{a}^{a+b}B\left( r \right) \mathrm {d}r \\[ 5pt ] &=& c \int _{a}^{a+b}\frac {\mu _{0}\mu _{\mathrm {r}}I}{2\pi r} \mathrm {d}r \\[ 5pt ] &=& \frac {\mu _{0}\mu _{\mathrm {r}}Ic}{2\pi } \int _{a}^{a+b}\frac {1}{r} \mathrm {d}r \\[ 5pt ] &=& \frac {\mu _{0}\mu _{\mathrm {r}}Ic}{2\pi } \left[ \ln r \right] _{a}^{a+b} \\[ 5pt ] &=& \frac {\mu _{0}\mu _{\mathrm {r}}Ic}{2\pi } \left\{ \ln \left( a+b\right) -\ln a \right\} \\[ 5pt ] &=& \frac {\mu _{0}\mu _{\mathrm {r}}Ic}{2\pi}\ln \frac {a+b}{a} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：カ
環状鉄心の断面積\( \ S \ \)は，
\[
\begin{eqnarray}
S &=&bc \\[ 5pt ] \end{eqnarray}
\] であり，環状鉄心の平均磁路長\( \ l \ \)は，
\[
\begin{eqnarray}
l &=&2\pi \left( a+\frac {b}{2}\right) \\[ 5pt ] \end{eqnarray}
\] であるから，磁気抵抗\( \ R_{\mathrm {m}} \ \)は，ワンポイント解説「2.磁気回路のオームの法則」の通り，
\[
\begin{eqnarray}
R_{\mathrm {m}} &=&\frac {l}{\mu _{0}\mu _{\mathrm {r}}S} \\[ 5pt ] &=&\frac {\displaystyle 2\pi \left( a+\frac {b}{2}\right) }{\mu _{0}\mu _{\mathrm {r}}bc} \\[ 5pt ] &=&\frac {\displaystyle \pi \left( 2a+b\right) }{\mu _{0}\mu _{\mathrm {r}}bc} \\[ 5pt ] &=&\frac {\pi }{\mu _{0}\mu _{\mathrm {r}}}\frac {2a+b}{bc} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：リ
磁気回路のオームの法則より，鉄心内の磁束\( \ \mathit {\Phi }_{\mathrm {mc}} \ \)は，
\[
\begin{eqnarray}
\mathit {\Phi }_{\mathrm {mc}} &=& \frac {I}{R_{\mathrm {m}}} \\[ 5pt ] &=& \frac {I}{\displaystyle \frac {\pi }{\mu _{0}\mu _{\mathrm {r}}}\frac {2a+b}{bc}} \\[ 5pt ] &=& \frac {\mu _{0}\mu _{\mathrm {r}}I}{\pi}\frac {bc}{2a+b} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ヲ
(2)解答式に\( \ a=2 \ \mathrm {cm},b=1 \ \mathrm {cm},c=1 \ \mathrm {cm}, \mu _{\mathrm {r}}=5 \ 000,I=1 \ \mathrm {kA},\mu _{0}=4\pi \times 10^{-7} \ \mathrm {H / m} \ \)を代入すると\( \ \mathit {\Phi }_{\mathrm {ampere}} \ \)は，
\[
\begin{eqnarray}
\mathit {\Phi }_{\mathrm {ampere}}&=& \frac {\mu _{0}\mu _{\mathrm {r}}Ic}{2\pi}\ln \frac {a+b}{a} \\[ 5pt ] &=& \frac {4\pi \times 10^{-7}\times 5 \ 000 \times 1\times 10^{3}\times 1\times 10^{-2}}{2\pi}\ln \frac {2\times 10^{-2}+1\times 10^{-2}}{2\times 10^{-2}} \\[ 5pt ] &=& 1\times 10^{-2}\times \ln 1.5 \\[ 5pt ] &≒& 1\times 10^{-2}\times 0.4 \\[ 5pt ] &=& 0.004 \ \mathrm {[Wb]}　→　4 \ \mathrm {[mWb]} \\[ 5pt ] \end{eqnarray}
\] となり，同様に(4)解答式に\( \ a=2 \ \mathrm {cm},b=1 \ \mathrm {cm},c=1 \ \mathrm {cm}, \mu _{\mathrm {r}}=5 \ 000,I=1 \ \mathrm {kA},\mu _{0}=4\pi \times 10^{-7} \ \mathrm {H / m} \ \)を代入すると\( \ \mathit {\Phi }_{\mathrm {mc}} \ \)は，
\[
\begin{eqnarray}
\mathit {\Phi }_{\mathrm {mc}} &=& \frac {\mu _{0}\mu _{\mathrm {r}}I}{\pi}\frac {bc}{2a+b} \\[ 5pt ] &=& \frac {4\pi \times 10^{-7}\times 5 \ 000 \times 1\times 10^{3}}{\pi}\frac {1\times 10^{-2}\times 1\times 10^{-2}}{2\times 2\times 10^{-2}+1\times 10^{-2}} \\[ 5pt ] &=& 0.004 \ \mathrm {[Wb]}　→　4 \ \mathrm {[mWb]} \\[ 5pt ] \end{eqnarray}
\] と求められる。