Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
次の文章は,半導体内の電気伝導に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選びなさい。なお,電子の電荷量(絶対値)を\( \ e \ \)とする。
断面積が\( \ S \ \),長さが\( \ l \ \)の円柱の\( \ \mathrm {n} \ \)形半導体の両端に,大きさが\( \ V \ \)の直流電圧を加えた。電圧によって半導体中に一様な電界が生成されるとすると,その電界\( \ E \ \)は,\( \ E= \ \fbox { (1) } \ \)であり,電子は力\( \ F= \ \fbox { (2) } \ \)で加速される。電子の有効質量を\( \ m^{*} \ \)とすると,電子の加速度は\( \ \fbox { (3) } \ \)となるが,散乱を考えると,電子の速度は最終的に電界に比例する平均速度\( \ v \ \)となる。\( \ v \ \)と電界の関係は,移動度\( \ \mu \ \)を用いて\( \ v=\mu E \ \)と表される。
半導体中の電子濃度を\( \ n \ \)とすると,この半導体を流れる電流は,\( \ v \ \)を用いて,\( \ I=\fbox { (4) } \ \)と表せる。そこで,電圧\( \ V \ \)と電流\( \ I \ \)の関係は\( \ I= \ \fbox { (5) } \ \)と表すことができる。
〔問4の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {eV}{m^{*}} &(ロ)& \frac {\mu nV}{l} &(ハ)& eVl \\[ 5pt ]
&(ニ)& evnS &(ホ)& vnS &(ヘ)& \frac {e\mu nVS}{l} \\[ 5pt ]
&(ト)& eVm^{*} &(チ)& \frac {e\mu nV}{l} &(リ)& eE \\[ 5pt ]
&(ヌ)& \frac {eE}{m^{*}} &(ル)& evn &(ヲ)& \frac {V}{l} \\[ 5pt ]
&(ワ)& Vl &(カ)& eV &(ヨ)& \frac {V}{S}
\end{eqnarray}
\]
【ワンポイント解説】
真空電子理論の公式をきちんと理解していれば,難なく解けると思いますが,(4)の電流密度\( \ J \ \)と電流\( \ I \ \)を間違えると(5)も間違えてしまうため,注意が必要です。
1.半導体中の電流\( \ I \ \)と電流密度\( \ J \ \)
断面積\( \ S \ \)の半導体に一様に電流が流れるとします。
半導体中の電子の電荷を\( \ e \ \),電子濃度を\( \ n \ \),平均速度を\( \ v \ \)とすると,電流密度\( \ J \ \)は,
\[
\begin{eqnarray}
J&=&evn \\[ 5pt ]
\end{eqnarray}
\]
となり,電流\( \ I \ \)は,
\[
\begin{eqnarray}
I &=& JS \\[ 5pt ]
&=& evnS \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)解答:ヲ
問題文の内容を整理すると,図1のようになる。
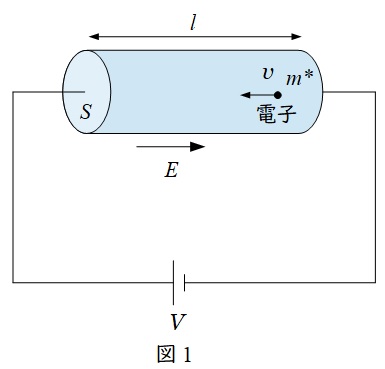
半導体中の電界は一様であるから,
\[
\begin{eqnarray}
E&=&\frac {V}{l} \\[ 5pt ]
\end{eqnarray}
\]
となる。
(2)解答:リ
電子の電荷量が\( \ e \ \)であるから,
\[
\begin{eqnarray}
F&=&eE \\[ 5pt ]
\end{eqnarray}
\]
となる。
(3)解答:ヌ
運動方程式より加速度を\( \ a \ \)とすると,\( \ F=m^{*}a \ \)の関係があるから,
\[
\begin{eqnarray}
a &=& \frac {F}{m^{*}} \\[ 5pt ]
&=& \frac {eE}{m^{*}} \\[ 5pt ]
\end{eqnarray}
\]
となる。
(4)解答:ニ
半導体中の電流を\( \ I \ \)とすると,ワンポイント解説の通り,
\[
\begin{eqnarray}
I&=&evnS \\[ 5pt ]
\end{eqnarray}
\]
となる。
(5)解答:ヘ
\( \ v=\mu E \ \),\( \ \displaystyle E=\frac {V}{l} \ \)であるから,
\[
\begin{eqnarray}
I &=& evnS \\[ 5pt ]
&=& e\mu EnS \\[ 5pt ]
&=& \frac {e\mu nVS}{l}
\end{eqnarray}
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは