Contents
【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,環状ソレノイドコイル中の磁界に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。なお,コイルが作り出す磁界は環状ソレノイドの円周方向を向いており,コイルの内部にのみ存在するものとする。
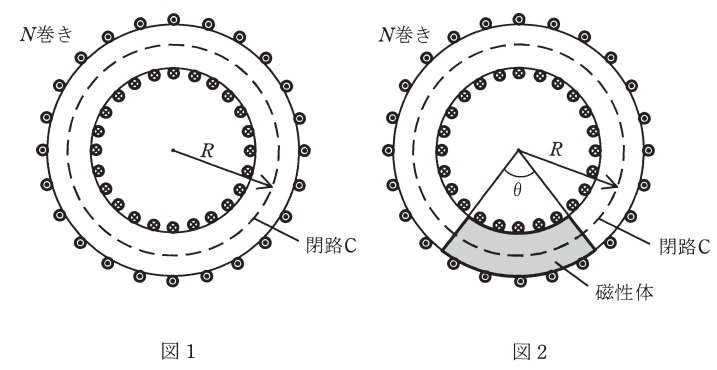
図1に示すように\( \ N \ \)巻きの巻線が密に巻かれた環状ソレノイドコイルを考える。コイル内部は真空(透磁率は\( \ \mu _{0} \ \))となっており,コイルに電流\( \ I \ \)が流れている。半径\( \ R \ \)の円周状の閉路\( \ \mathrm {C} \ \)に沿ってアンペールの法則を適用すると,閉路\( \ \mathrm {C} \ \)上の磁束密度は\( \ B=\fbox { (1) } \ \)となり,\( \ R \ \)の増加に対して\( \ \fbox { (2) } \ \)。
次に,図2に示すように環状ソレノイドコイルの内部の角度\( \ \theta \ \)の領域を透磁率\( \ \mu \ \)の磁性体(ただし,\( \ \mu > \mu _{0} \ \))で満たす。真空領域と磁性体領域で磁束密度は一定であると考えられるので、真空領域の磁界\( \ H_{0} \ \)と磁性体領域の磁界\( \ H_{1} \ \)の比は\( \ H_{0}:H_{1}=\fbox { (3) } \ \)となり,磁性体中には真空領域の磁束密度と\( \ \fbox { (4) } \ \)向きの磁化\( \ M \ \)が発生する。コイルに流れる電流\( \ I \ \)とすると,閉路\( \ \mathrm {C} \ \)上の磁束密度は\( \ \fbox { (5) } \ \)となる。
〔問2の解答群〕
\[
\begin{eqnarray}
&(イ)& \mu : \mu _{0} &(ロ)& \frac {\mu _{0} NI}{2\pi} &(ハ)& Bの値は減少する \\[ 5pt ]
&(ニ)& 1:1 &(ホ)& \frac {\mu _{0} NI}{2\pi R} &(ヘ)& 垂直な \\[ 5pt ]
&(ト)& Bの値は増加する &(チ)& \frac {NI^{2}}{\displaystyle \frac {\theta R}{\mu }+\frac {\left( 2\pi -\theta \right) R}{\mu _{0}}} &(リ)& 同じ \\[ 5pt ]
&(ヌ)& \left[\theta R \mu +\left( 2\pi -\theta \right) R\mu _{0} \right] NI &(ル)& \mu_{0} : \mu &(ヲ)& 2\pi R\mu _{0} NI \\[ 5pt ]
&(ワ)& Bの値は変化しない &(カ)& \frac {NI}{\displaystyle \frac {\theta R}{\mu }+\frac {\left( 2\pi -\theta \right) R}{\mu _{0}}} &(ヨ)& 逆
\end{eqnarray}
\]
【ワンポイント解説】
環状ソレノイド自体が出題されにくい問題ですが,本問ではそこに磁性体を挿入するため,難易度がやや高くなっています。
1.アンペールの周回積分の法則
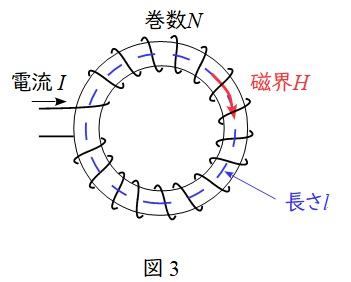
図3の示すような,電流\( \ I \ \)が流れている環状ソレノイドの中心に発生する磁界の大きさ\( \ H \ \)には,アンペールの周回積分の法則が適用され,
\[
\begin{eqnarray}
NI&=&\int H \mathrm {d}l \\[ 5pt ]
\end{eqnarray}
\]
が成立します。本問においては,
\[
\begin{eqnarray}
NI=2\pi R H ⇔ H=\frac {NI}{2\pi R} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.磁束密度\( \ B \ \)と磁界の強さ\( \ H \ \)の関係
透磁率が\( \ \mu \ \)の時,磁束密度\( \ B \ \)と磁界の大きさ\( \ H \ \)の関係は,
\[
\begin{eqnarray}
B&=&\mu H \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)解答:ホ
図1での磁界の強さ\( \ H \ \)とすると,ワンポイント解説「1.アンペールの周回積分の法則」より,
\[
\begin{eqnarray}
NI&=&2\pi R H \\[ 5pt ]
\end{eqnarray}
\]
であるから,
\[
\begin{eqnarray}
H&=&\frac {NI}{2\pi R} \\[ 5pt ]
\end{eqnarray}
\]
となる。ワンポイント解説「2.磁束密度\( \ B \ \)と磁界の強さ\( \ H \ \)の関係」より,
\[
\begin{eqnarray}
B&=&\mu _{0}H \\[ 5pt ]
&=&\frac {\mu _{0}NI}{2\pi R} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ハ
(1)の解答式より,\( \ \displaystyle B\propto \frac {1}{R} \ \)であるから,\( \ R \ \)の増加に対して,\( \ B \ \)は反比例して減少する。
(3)解答:イ
ワンポイント解説「2.磁束密度\( \ B \ \)と磁界の強さ\( \ H \ \)の関係」から,
\[
\begin{eqnarray}
H_{0}&=&\frac {B}{\mu _{0}} &・・・・・・・・・・ ①& \\[ 5pt ]
H_{1}&=&\frac {B}{\mu } &・・・・・・・・・・ ②& \\[ 5pt ]
\end{eqnarray}
\]
となるから,
\[
\begin{eqnarray}
H_{0}:H_{1}&=&\frac {B}{\mu _{0}}:\frac {B}{\mu } \\[ 5pt ]
\end{eqnarray}
\]
となる。双方に,\(\displaystyle \frac {\mu _{0} \mu }{B}\)を掛けると,
\[
\begin{eqnarray}
H_{0}:H_{1}&=&{\mu }:{\mu _{0}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:リ
(3)より\( \ H_{0} > H_{1} \ \)となるから,磁性体には磁界(磁束密度)と同方向の磁化が発生する。
(5)解答:カ
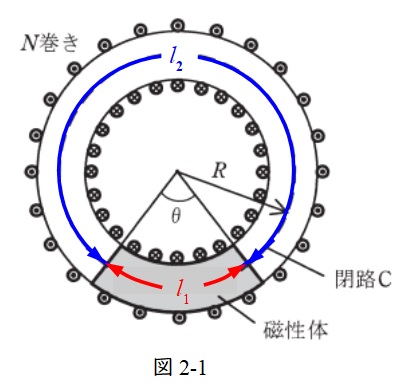
図2-1の通り,磁性体内の長さを\( \ l_{1} \ \),真空領域の長さを\( \ l_{2} \ \)とすると,
\[
\begin{eqnarray}
l_{1} &=& 2\pi R \times \frac {\theta }{2\pi } \\[ 5pt ]
&=& \theta R \\[ 5pt ]
l_{2} &=& 2\pi R \times \frac {2\pi -\theta }{2\pi } \\[ 5pt ]
&=& \left( 2\pi -\theta \right)R \\[ 5pt ]
\end{eqnarray}
\]
となる。ワンポイント解説「1.アンペールの周回積分の法則」より,より,
\[
\begin{eqnarray}
NI &=& \int H \mathrm {d}l \\[ 5pt ]
&=& \int H_{1} \mathrm {d}l_{1} +\int H_{0} \mathrm {d}l_{2} \\[ 5pt ]
&=& H_{1} l_{1}+H_{0} l_{2} \\[ 5pt ]
\end{eqnarray}
\]
であり,①,②より\( \ \displaystyle H_{0}=\frac {B}{\mu _{0}},H_{1}=\frac {B}{\mu } \ \)であるから,
\[
\begin{eqnarray}
NI&=&\frac {B}{\mu }\theta R+\frac {B}{\mu _{0}}\left( 2\pi -\theta \right)R \\[ 5pt ]
\end{eqnarray}
\]
となる。\( \ B \ \)について整理すると,
\[
\begin{eqnarray}
B&=&\frac {NI}{\displaystyle \frac {\theta R}{\mu }+\frac {\left( 2\pi -\theta \right) R}{\mu _{0}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは