Contents
【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,正弦波交流電圧源に接続された,抵抗終端リアクタンス回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
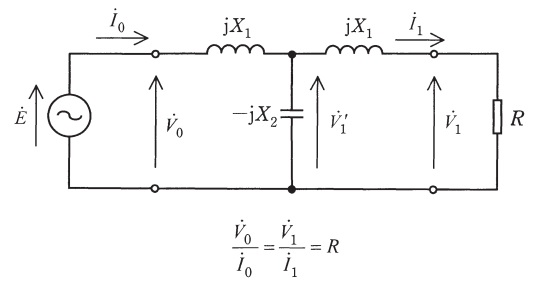
図のように,抵抗\( \ R \ \)で終端した\( \ 2 \ \)端子対リアクタンス回路に正弦波交流電圧源\( \ \dot E \ \)を接続すると,回路の端子対で等式\( \ \displaystyle \frac {\dot V_{0}}{\dot I_{0}}=\frac {\dot V_{1}}{\dot I_{1}}=R \ \)が成立した。\( \ \displaystyle \frac {\dot V_{0}}{\dot I_{0}}=\frac {\dot V_{1}}{\dot I_{1}}=R \ \)を満たす素子値\( \ X_{1} \ \),\( \ X_{2} \ \),\( \ R \ \)の組み合わせは,\( \ X_{1}\neq X_{2} \ \)の場合も含めて無数に存在する。このとき,図の\( \ -jX_{2} \ \)に現れる電圧を\( \ \dot V_{1}’ \ \)とおくと,電圧の比\( \ \displaystyle \frac {\dot V_{1}’}{\dot V_{0}} \ \),\( \ \displaystyle \frac {\dot V_{1}}{\dot V_{1}’} \ \)はインピーダンスの比により,
\[
\begin{eqnarray}
&&\frac {\dot V_{1}’}{\dot V_{0}}=\frac {\fbox { (1) }}{R} ,\frac {\dot V_{1}}{\dot V_{1}’}=\frac {R}{\fbox { (2) }} ・・・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
で与えられる。
もし,リアクタンス回路の素子値が\( \ X_{1}=X_{2}=\sqrt {3} \Omega \ \)なら,\( \ \displaystyle \frac {\dot V_{0}}{\dot I_{0}}=\frac {\dot V_{1}}{\dot I_{1}}=R \ \)より,\( \ R=\fbox { (3) } \ \Omega \ \)であり,電圧の比\( \ \displaystyle \frac {\dot V_{1}}{\dot V_{0}} \ \)は
\[
\begin{eqnarray}
&&\frac {\dot V_{1}}{\dot V_{0}}=\frac {\fbox { (1) }}{\fbox { (2) }}=\mathrm {e}^{\mathrm {j} \ \fbox { (4) }} ・・・・・・・・・・・ ② \\[ 5pt ]
\end{eqnarray}
\]
となる。電圧\( \ \dot V_{0} \ \),\( \ \dot V_{1}’ \ \),\( \ \dot V_{1} \ \)の大きさの関係は,①,②式より\( \ \fbox { (5) } \ \)となる。
〔問3の解答群〕
\[
\begin{eqnarray}
&(イ)& \left| \dot V_{0} \right|=\left| \dot V_{1} \right|=\left| \dot V_{1}’ \right| &(ロ)& -\frac {\pi }{4} &(ハ)& R-\mathrm {j}X_{2} \\[ 5pt ]
&(ニ)& \frac {\pi }{3} &(ホ)& R+\mathrm {j}\left( X_{2}-X_{1}\right) &(ヘ)& \left| \dot V_{0} \right|=\left| \dot V_{1} \right|>\left| \dot V_{1}’ \right| \\[ 5pt ]
&(ト)& 1 &(チ)& R-\mathrm {j}X_{1} &(リ)& R+\mathrm {j}\left( X_{1}-X_{2}\right) \\[ 5pt ]
&(ヌ)& \left| \dot V_{0} \right|=\left| \dot V_{1} \right|<\left| \dot V_{1}' \right| &(ル)& 2 &(ヲ)& R+\mathrm {j}X_{1} \\[ 5pt ]
&(ワ)& R+\mathrm {j}X_{2} &(カ)& -\frac {\pi }{2} &(ヨ)& \sqrt {3}
\end{eqnarray}
\]
【ワンポイント解説】
普通の電気回路ではなく,二種らしくやや特殊な問題となっている上計算量も多いため,難易度がやや高めです。キルヒホッフの法則以外に本問では以下の公式を使用します。
1.オイラーの公式
オイラーの公式は,
\[
\begin{eqnarray}
\mathrm {e}^{\mathrm {j}\theta }&=&\cos \theta + \mathrm {j}\sin \theta \\[ 5pt ]
\end{eqnarray}
\]
となり,例えば,
\[
\begin{eqnarray}
\mathrm {e}^{-\mathrm {j}\frac {\pi }{2} } &=& \cos \left( -\frac {\pi }{2}\right) + \mathrm {j}\sin \left( -\frac {\pi }{2}\right) \\[ 5pt ]
&=& 0+\mathrm {j}(-1)\\[ 5pt ]
&=& -\mathrm {j}
\end{eqnarray}
\]
となります。
【解答】
(1)解答:チ
キルヒホッフの法則より,\( \ \dot V_{1}’ \ \)を\( \ \dot V_{0} \ \),\( \ \dot I_{0} \ \)を用いて表すと,
\[
\begin{eqnarray}
\dot V_{1}’&=&\dot V_{0}-\mathrm {j}X_{1}\dot I_{0} ・・・・・・・・・・・ ③ \\[ 5pt ]
\end{eqnarray}
\]
となる。題意より,\( \ \displaystyle \frac {\dot V_{0}}{\dot I_{0}}=R \ \)すなわち\( \ \displaystyle {\dot I_{0}}=\frac {\dot V_{0}}{R} \ \)であるから,これを上式に代入すると,
\[
\begin{eqnarray}
\dot V_{1}’ &=& \dot V_{0}-\mathrm {j}X_{1}\frac {\dot V_{0}}{R} \\[ 5pt ]
\frac {\dot V_{1}’}{\dot V_{0}} &=& 1-\frac {\mathrm {j} X_{1}}{R} \\[ 5pt ]
\frac {\dot V_{1}’}{\dot V_{0}} &=& \frac {R-\mathrm {j} X_{1}}{R} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ヲ
(1)と同様にキルヒホッフの法則より,\( \ \dot V_{1}’ \ \)を\( \ \dot V_{1} \ \),\( \ \dot I_{1} \ \)を用いて表すと,
\[
\begin{eqnarray}
\dot V_{1}’&=&\dot V_{1}+\mathrm {j}X_{1}\dot I_{1} ・・・・・・・・・・・ ④ \\[ 5pt ]
\end{eqnarray}
\]
となる。題意より,\( \ \displaystyle \frac {\dot V_{1}}{\dot I_{1}}=R \ \)すなわち\( \ \displaystyle {\dot I_{1}}=\frac {\dot V_{1}}{R} \ \)であるから,これを上式に代入すると,
\[
\begin{eqnarray}
\dot V_{1}’ &=& \dot V_{1}+\mathrm {j}X_{1}\frac {\dot V_{1}}{R} \\[ 5pt ]
\dot V_{1}’ &=& \frac {R+\mathrm {j} X_{1}}{R}\dot V_{1} \\[ 5pt ]
\frac {\dot V_{1}}{\dot V_{1}’} &=& \frac {R}{R+\mathrm {j} X_{1}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ヨ
\( \ -\mathrm {j}X_{2} \ \)を流れる電流は\( \ \dot I_{0}-\dot I_{1} \ \)であるから,
\[
\begin{eqnarray}
\dot V_{1}’&=&-\mathrm {j}X_{2}\left( \dot I_{0}-\dot I_{1}\right) ・・・・・・・・・ ⑤ \\[ 5pt ]
\end{eqnarray}
\]
である。次に,③,④を変形する。
\[
\begin{eqnarray}
\dot V_{1}’&=&\dot V_{0}-\mathrm {j}X_{1}\dot I_{0} &・・・・・・・・・・・ ③& \\[ 5pt ]
\dot V_{1}’&=&\dot V_{1}+\mathrm {j}X_{1}\dot I_{1} &・・・・・・・・・・・ ④& \\[ 5pt ]
\end{eqnarray}
\]
であり,題意より\( \ \dot V_{0}=R\dot I_{0} \ \),\( \ \dot V_{1}=R\dot I_{1} \ \)であるため,
\[
\begin{eqnarray}
\dot V_{1}’ &=& R\dot I_{0}-\mathrm {j}X_{1}\dot I_{0} \\[ 5pt ]
&=& \left( R-\mathrm {j}X_{1}\right) \dot I_{0} \\[ 5pt ]
\dot I_{0} &=& \frac {\dot V_{1}’}{R-\mathrm {j}X_{1}} ・・・・・・・・・・・・ ③’ \\[ 5pt ]
\dot V_{1}’ &=& R\dot I_{1}+\mathrm {j}X_{1}\dot I_{1} \\[ 5pt ]
&=& \left( R+\mathrm {j}X_{1}\right) \dot I_{1} \\[ 5pt ]
\dot I_{1} &=& \frac {\dot V_{1}’}{R+\mathrm {j}X_{1}} ・・・・・・・・・・・・ ④’ \\[ 5pt ]
\end{eqnarray}
\]
となる。\(③’,④’\)を⑤に代入すると,
\[
\begin{eqnarray}
\dot V_{1}’&=&-\mathrm {j}X_{2}\left( \frac {\dot V_{1}’}{R-\mathrm {j}X_{1}}-\frac {\dot V_{1}’}{R+\mathrm {j}X_{1}}\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,両辺\( \ \dot V_{1}’ \ \)で割って\( \ R \ \)について整理すると,
\[
\begin{eqnarray}
1 &=& -\mathrm {j}X_{2}\left( \frac {1}{R-\mathrm {j}X_{1}}-\frac {1}{R+\mathrm {j}X_{1}}\right) \\[ 5pt ]
1 &=& -\mathrm {j}X_{2}\left[ \frac {\left( R+\mathrm {j}X_{1}\right) -\left( R-\mathrm {j}X_{1}\right) }{\left( R-\mathrm {j}X_{1}\right) \left( R+\mathrm {j}X_{1}\right) }\right] \\[ 5pt ]
1 &=& -\mathrm {j}X_{2}\left( \frac {\mathrm {j}2X_{1} }{R^{2}+X_{1}^{2} }\right) \\[ 5pt ]
1 &=& \frac {2X_{1}X_{2}}{R^{2}+X_{1}^{2} } \\[ 5pt ]
R^{2}+X_{1}^{2} &=& 2X_{1}X_{2} \\[ 5pt ]
R^{2} &=& 2X_{1}X_{2}-X_{1}^{2} \\[ 5pt ]
R &=& \sqrt {2X_{1}X_{2}-X_{1}^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,\( \ X_{1}=X_{2}=\sqrt {3} \ \)を代入すれば,
\[
\begin{eqnarray}
R&=&\sqrt {2\times \sqrt {3}\times \sqrt {3}-\left( \sqrt {3}\right) ^{2}} \\[ 5pt ]
&=&\sqrt {3} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:カ
題意より,\( \ \displaystyle\frac {\dot V_{1}}{\dot V_{0}}=\frac {R-\mathrm {j} X_{1}}{R+\mathrm {j} X_{1}} \ \)であり,これに\( \ R=X_{1}=\sqrt {3} \ \)を代入すると,
\[
\begin{eqnarray}
\frac {\dot V_{1}}{\dot V_{0}} &=& \frac {\sqrt {3}-\mathrm {j} \sqrt {3}}{\sqrt {3}+\mathrm {j} \sqrt {3}} \\[ 5pt ]
&=& \frac {1-\mathrm {j}}{1+\mathrm {j}}
\end{eqnarray}
\]
となり,さらに分母分子に\( \ 1-\mathrm {j} \ \)を掛けると,
\[
\begin{eqnarray}
\frac {\dot V_{1}}{\dot V_{0}} &=& \frac {\left( 1-\mathrm {j}\right) \left( 1-\mathrm {j}\right) }{\left( 1+\mathrm {j}\right) \left( 1-\mathrm {j}\right) } \\[ 5pt ]
&=& \frac {1-\mathrm {j}2-1}{1+1} \\[ 5pt ]
&=& -\mathrm {j}
\end{eqnarray}
\]
と求められる。よって,ワンポイント解説「2.オイラーの公式」より\(\displaystyle -\mathrm {j}=e^{-\mathrm {j}\frac {\pi }{2} }\)となる。
(5)解答:ヌ
\( \ \dot V_{0} \ \)を基準とすると,(1),(4)の解答より,
\[
\begin{eqnarray}
\dot V_{1}’ &=& \frac {R-\mathrm {j} X_{1}}{R}\dot V_{0} \\[ 5pt ]
&=& \frac {\sqrt {3}-\mathrm {j} \sqrt {3}}{\sqrt {3}}\dot V_{0} \\[ 5pt ]
&=& \left( 1-\mathrm {j}\right)\dot V_{0} \\[ 5pt ]
\dot V_{1}&=&-\mathrm {j}\dot V_{0} \\[ 5pt ]
\end{eqnarray}
\]
であるから,
\[
\begin{eqnarray}
\left| \dot V_{1}’\right| &=& \sqrt {1^{2}+1^{2}}\left| \dot V_{0}\right| \\[ 5pt ]
&=& \sqrt {2}\left| \dot V_{0}\right| \\[ 5pt ]
\left| \dot V_{1}\right| &=& \sqrt {1^{2}}\left| \dot V_{0}\right| \\[ 5pt ]
&=& \left| \dot V_{0}\right| \\[ 5pt ]
\end{eqnarray}
\]
となり,
\[
\begin{eqnarray}
\left| \dot V_{0} \right|=\left| \dot V_{1} \right|<\left| \dot V_{1}' \right| \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは