《理論》〈電気及び電子計測〉[R05:問8]熱電形の交流電力計の測定原理に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

次の文章は，熱電形の交流電力計に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。

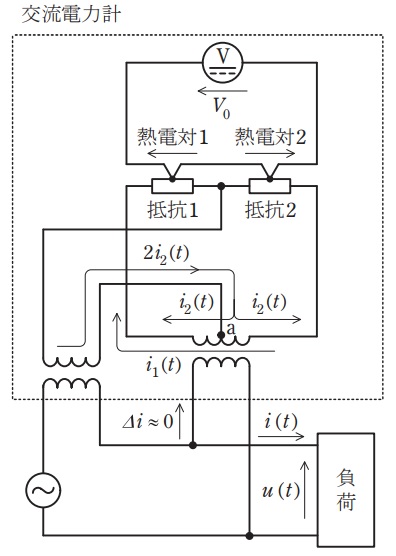
図示した交流電力計は，理想変圧器，理想変流器，抵抗値がともに\( \ R \ \)である二つの抵抗，二つの熱電対及び直流電圧計で構成されている。なお，変圧器の一次巻線に流れる電流\( \ \mathit {\Delta }i \ \)は十分小さい。また，節点\( \ \mathrm {a} \ \)は変圧器の二次巻線の中点である。

時刻\( \ t \ \)における負荷への入力電圧\( \ u\left( t\right) \ \)及び電流\( \ i\left( t\right) \ \)を次式で表すものとする。なお，電圧に対する電流の位相角を\( \ \theta \ \)，角周波数及び周期をそれぞれ\( \ \omega \ \)及び\( \ T \ \)で表す。
\[
\begin{eqnarray}
u\left( t\right) &=& \sqrt {2}U \sin \omega t \\[ 5pt ] i\left( t\right) &=& \sqrt {2}I \sin \left( \omega t -\theta \right) \\[ 5pt ] \end{eqnarray}
\] 熱電対とは，異種の金属同士を接続し，その接点に温度差を与えたときに熱起電力が生じる\( \ \fbox {　 （１） 　} \ \)効果を応用した温度センサである。本回路では，抵抗のジュール熱によって生じる温度上昇に比例した直流電圧に変換している。なお，二つの熱電対は同形式であり，図中の「熱電対\( \ 1 \ \)」「熱電対\( \ 2 \ \)」の下に記した矢印の向きに起電力が生じるように接続されている。

\( \ i_{1} \left( t\right) \ \)は，時刻\( \ t \ \)における理想変圧器の二次電圧と抵抗から定まる電流であり，\( \ u \left( t\right) \ \)すなわち理想変圧器の一次電圧に比例する。また，\( \ 2i_{2} \left( t\right) \ \)は，時刻\( \ t \ \)における理想変流器の二次電流であり，\( \ i \left( t\right) \ \)すなわち理想変流器の一次電流に比例する。

まず，\( \ i_{1} \left( t\right) \ \)及び\( \ i_{2} \left( t\right) \ \)を用いて抵抗\( \ 1 \ \)及び抵抗\( \ 2 \ \)で消費する電力を求めると，それぞれ\( \ \fbox {　 （２） 　} \ \)及び\( \ \fbox {　 （３） 　} \ \)となる。各抵抗では電力消費に伴い温度が上昇することから，熱電対\( \ 1 \ \)及び熱電対\( \ 2 \ \)に起電力が生じ，直流電圧計は次式に示す\( \ V_{0} \ \)を指示する。
\[
\begin{eqnarray}
V_{0}&∝& \ \fbox {　 （２） 　} \ – \ \fbox {　 （３） 　} \ = \ \fbox {　 （４） 　} \ \\[ 5pt ] \end{eqnarray}
\] \( \ u \left( t\right) \ \)と\( \ i_{1} \left( t\right) \ \)，\( \ i \left( t\right) \ \)と\( \ i_{2} \left( t\right) \ \)が比例関係にあることを考慮すると，\( \ V_{0} \ \)は次式に示したとおり負荷の消費電力に比例する。
\[
\begin{eqnarray}
V_{0}&∝&\frac {1}{T}\int _{0}^{T} \ \fbox {　 （５） 　} \ \mathrm {d}T=UI \cos \theta \\[ 5pt ] \end{eqnarray}
\] 以上が，熱電形の交流電力計の測定原理である。

〔問8の解答群〕
\[
\begin{eqnarray}
&（イ）&　ペルチェ　　　　　&（ロ）&　ホール　　　　　&（ハ）&　ゼーベック \\[ 5pt ] &（ニ）&　\frac {R}{T}\int _{0}^{T} \left[ i_{1}\left( t\right) -i_{2}\left( t\right) \right] \mathrm {d}t　　　　　&（ホ）&　\frac {1}{RT}\int _{0}^{T} \left[ i_{1}\left( t\right) -i_{2}\left( t\right) \right] ^{2} \mathrm {d}t　　　　　&（ヘ）&　\frac {4}{RT}\int _{0}^{T} i_{1}\left( t\right) i_{2}\left( t\right) \mathrm {d}t \\[ 5pt ] &（ト）&　\frac {R}{T}\int _{0}^{T} \left[ i_{1}\left( t\right) +i_{2}\left( t\right) \right] \mathrm {d}t　　　　　&（チ）&　\frac {4R}{T}\int _{0}^{T} i_{1}\left( t\right) i_{2}\left( t\right) \mathrm {d}t　　　　　&（リ）&　\frac {R}{T}\int _{0}^{T} \left[ i_{1}\left( t\right) +i_{2}\left( t\right) \right] ^{2} \mathrm {d}t \\[ 5pt ] &（ヌ）&　\frac {2R}{T}\int _{0}^{T} i_{2}\left( t\right) \mathrm {d}t　　　　　&（ル）&　\frac {R}{T}\int _{0}^{T} \left[ i_{1}\left( t\right) -i_{2}\left( t\right) \right] ^{2} \mathrm {d}t　　　　　&（ヲ）&　\frac {1}{RT}\int _{0}^{T} \left[ i_{1}\left( t\right) +i_{2}\left( t\right) \right] ^{2} \mathrm {d}t \\[ 5pt ] &（ワ）&　u \left( t\right) i \left( t\right) 　　　　　&（カ）&　i_{2}^{2} \left( t\right) 　　　　　&（ヨ）&　i_{1}^{2} \left( t\right) \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

熱電形の交流電力計の測定原理を数式で導き出す問題です。
（１）は知識問題ですが，そこからは長い問題文を読解し，計算を進めていく能力が求められます。
慌てずに落ち着いて解くことが重要です。

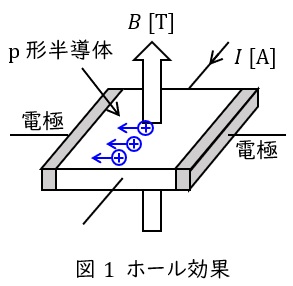
1.ホール効果
半導体に直流電流を流し，さらに半導体の表面に対して垂直に磁界をかけると，フレミングの左手の法則により半導体内の正孔及び電子に力が加わり，主に多数キャリヤが移動することで半導体の内部に電界が生じる現象です。

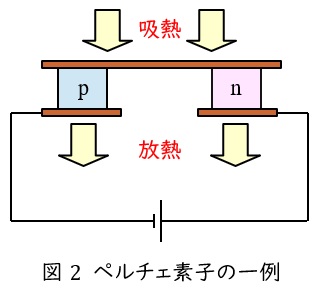
2.ペルチェ効果
異なる金属や半導体を接合して，電圧をかけると，吸熱もしくは発熱を発生する現象です。図2が代表的な半導体を使用したペルチェ素子で，電流の向きを逆にすると，発熱と吸熱も入れ替わります。

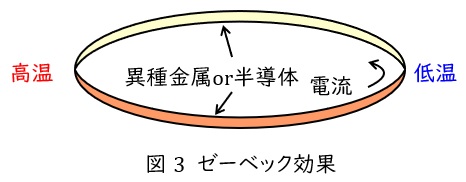
3.ゼーベック効果
異なる金属や半導体を図3のように接合して閉回路を作り，一端を高温（温接点），もう一端を低温（冷接点）とすると，熱起電力が発生し電流が流れる現象を言います。

4.平均値と実効値の定義
\( \ f( \theta ) \ \)を周期\( \ T \ \)の周期関数であるとしたとき，平均値と実効値は以下の通りとなります。
①平均値\( \ F_{\mathrm {av}} \ \)
定義式は，
\[
\begin{eqnarray}
F_{\mathrm {av}}&=&\frac {1}{T}\int _{0}^{T}f( \theta ) \mathrm {d}\theta \\[ 5pt ] \end{eqnarray}
\] であり，これを正弦波\( \ v\left( t \right) =V_{\mathrm {m}}\sin \omega t \ \)に適用すると，
\[
\begin{eqnarray}
V_{\mathrm {av}} &=&\frac {1}{\pi }\int _{0}^{\pi }V_{\mathrm {m}}\sin \omega t \mathrm {d}\omega t \\[ 5pt ] &=&\frac {V_{\mathrm {m}}}{\pi }\left[ -\cos \omega t \right] _{0}^{\pi } \\[ 5pt ] &=&\frac {V_{\mathrm {m}}}{\pi }\left[ 1+1 \right] \\[ 5pt ] &=&\frac {2}{\pi }V_{\mathrm {m}}
\end{eqnarray}
\] となります。

②実効値\( \ F \ \)　
定義式は，
\[
\begin{eqnarray}
F&=&\sqrt {\frac {1}{T} \int _{0}^{T} f( \theta ) ^{2} \mathrm {d}\theta } \\[ 5pt ] \end{eqnarray}
\] であり，これを正弦波\( \ v\left( t \right) =V_{\mathrm {m}}\sin \omega t \ \)に適用すると，
\[
\begin{eqnarray}
V &=&\sqrt {\frac {1}{\pi }\int _{0}^{\pi }{V_{\mathrm {m}}}^{2}\sin ^{2}\omega t \mathrm {d}\omega t} \\[ 5pt ] &=&V_{\mathrm {m}}\sqrt {\frac {1}{\pi }\int _{0}^{\pi }\frac {1-\cos 2\omega t}{2} \mathrm {d}\omega t} \\[ 5pt ] &=&V_{\mathrm {m}}\sqrt {\frac {1}{\pi }\left[ \frac {1}{2}\omega t -\frac {1}{4}\sin 2\omega t \right] _{0}^{\pi } } \\[ 5pt ] &=&V_{\mathrm {m}}\sqrt {\frac {1}{\pi }\left[ \frac {1}{2}\pi -0 -0 +0 \right] _{0}^{\pi } } \\[ 5pt ] &=&\frac {V_{\mathrm {m}}}{\sqrt {2}}
\end{eqnarray}
\] となります。

【解答】

(1)解答：ハ
題意より解答候補は，（イ）ペルチェ，（ロ）ホール，（ハ）ゼーベック，になると思います。
ワンポイント解説「3.ゼーベック効果」の通り，異種の金属同士を接続し，その接点に温度差を与えたときに熱起電力が生じるのはゼーベック効果といいます。

(2)解答：リ
問題図より，抵抗\( \ 1 \ \)に流れる電流は\( \ i_{1} \left( t\right) +i_{2} \left( t\right) \ \)であり，抵抗値は\( \ R \ \)であるから，時刻\( \ t \ \)における抵抗\( \ 1 \ \)での消費電力\( \ P_{1}\left( t \right) \ \)の瞬時値は，
\[
\begin{eqnarray}
P_{1}\left( t \right) &=&R\left\{ i_{1} \left( t\right) +i_{2} \left( t\right) \right\} ^{2} \\[ 5pt ] \end{eqnarray}
\] となるので，その平均値\( \ P_{\mathrm {1a}}\left( t \right) \ \)は，ワンポイント解説「4.平均値と実効値の定義」より，
\[
\begin{eqnarray}
P_{\mathrm {1a}}\left( t \right) &=&\frac {1}{T}\int _{0}^{T}P_{1}\left( t \right) \mathrm {d}t \\[ 5pt ] &=&\frac {1}{T}\int _{0}^{T} R\left\{ i_{1} \left( t\right) +i_{2} \left( t\right) \right\} ^{2}\mathrm {d}t \\[ 5pt ] &=&\frac {R}{T}\int _{0}^{T} \left\{ i_{1} \left( t\right) +i_{2} \left( t\right) \right\} ^{2}\mathrm {d}t \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ル
(2)と同様に，抵抗\( \ 2 \ \)に流れる電流は\( \ i_{1} \left( t\right) -i_{2} \left( t\right) \ \)であるから，抵抗\( \ 2 \ \)での消費電力の平均値\( \ P_{\mathrm {2a}}\left( t \right) \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {2a}}\left( t \right) &=&\frac {R}{T}\int _{0}^{T} \left\{ i_{1} \left( t\right) -i_{2} \left( t\right) \right\} ^{2}\mathrm {d}t \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：チ
（２）及び（３）解答式より，
\[
\begin{eqnarray}
V_{0}&∝&\frac {R}{T}\int _{0}^{T} \left\{ i_{1} \left( t\right) +i_{2} \left( t\right) \right\} ^{2}\mathrm {d}t -\frac {R}{T}\int _{0}^{T} \left\{ i_{1} \left( t\right) -i_{2} \left( t\right) \right\} ^{2}\mathrm {d}t \\[ 5pt ] &=&\frac {R}{T}\int _{0}^{T} \left[ \left\{ i_{1} \left( t\right) +i_{2} \left( t\right) \right\} ^{2}- \left\{ i_{1} \left( t\right) -i_{2} \left( t\right) \right\} ^{2}\right] \mathrm {d}t \\[ 5pt ] &=&\frac {R}{T}\int _{0}^{T} \left[ \left\{ {i_{1} \left( t\right) }^{2}+2i_{1} \left( t\right) i_{2} \left( t\right) +{i_{2} \left( t\right) }^{2}\right\} – \left\{ {i_{1} \left( t\right) }^{2}-2i_{1} \left( t\right) i_{2} \left( t\right) +{i_{2} \left( t\right) }^{2}\right\} \right] \mathrm {d}t \\[ 5pt ] &=&\frac {R}{T}\int _{0}^{T} 4i_{1} \left( t\right)i_{2} \left( t\right) \mathrm {d}t \\[ 5pt ] &=&\frac {4R}{T}\int _{0}^{T} i_{1} \left( t\right)i_{2} \left( t\right) \mathrm {d}t \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ワ
題意より，\( \ i_{1} \left( t\right) =k_{1}u \left( t\right) \ \)及び\( \ i_{2} \left( t\right) =k_{2}i \left( t\right) \ \)（ただし，\( \ k_{1} \ \)及び\( \ k_{2} \ \)は定数）とおけるので，それぞれ（４）解答式に代入すると，
\[
\begin{eqnarray}
V_{0}&∝&\frac {4R}{T}\int _{0}^{T} i_{1} \left( t\right)i_{2} \left( t\right) \mathrm {d}t \\[ 5pt ] &=&\frac {4R}{T}\int _{0}^{T} k_{1}u \left( t\right) \cdot k_{2}i \left( t\right) \mathrm {d}t \\[ 5pt ] &=&\frac {4k_{1}k_{2}R}{T}\int _{0}^{T} u \left( t\right) i \left( t\right) \mathrm {d}t \\[ 5pt ] &∝&\frac {1}{T}\int _{0}^{T} u \left( t\right) i \left( t\right) \mathrm {d}t \\[ 5pt ] \end{eqnarray}
\] と求められる。