《機械・制御》〈回転機〉[H22:問1]三相突発短絡試験による同期発電機の定数測定法に関する論説問題

【問題】

【難易度】★★★★★（難しい）

三相突発短絡試験による円筒界磁形同期発電機の定数測定法に関して，次の問に答えよ。

(1)　三相突発短絡試験による定数測定法とは，同期発電機を無負荷定格回転速度で運転し，電機子定格電圧の$\ 15～30 \ \mathrm {％} \ $の電圧が発生した状態で電機子端子三相を開閉器で突発短絡し，電機子電流及び界磁電流の変化をオシログラフで記録し，直軸初期過渡リアクタンス，直軸過渡リアクタンス，短絡初期過渡時定数及び短絡過渡時定数を求める方法である。

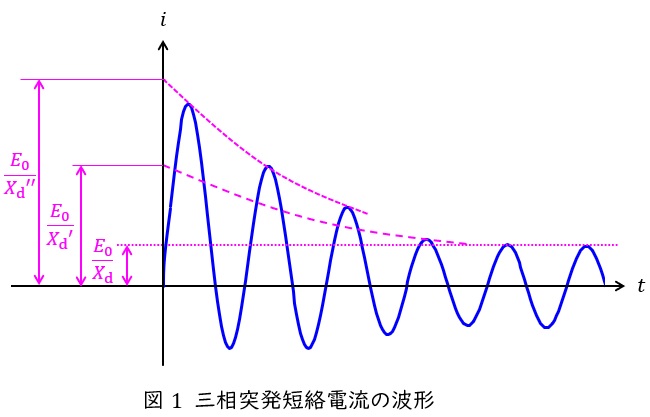
無負荷で電圧が発生している同期発電機の端子を三相突発短絡させた場合の突発短絡相電流$\ i_{\mathrm {ph}} \ $は次式で表され，交流分の振幅は大きな初期過渡状態から時間の経過とともに減衰して過渡状態を経て持続短絡状態になる。
$$\begin{eqnarray} i_{\mathrm {ph}}&=&\left[ \left( \ \fbox {$\hskip 1em $ $\mathrm {A}$ $\hskip 1em $} \ \right) \mathrm {exp} \left( \frac {-t}{T_{\mathrm {d}}^{\prime \prime }}\right) +\left( \ \fbox {$\hskip 1em $ $\mathrm {B}$ $\hskip 1em $} \ \right) \mathrm {exp} \left( \frac {-t}{T_{\mathrm {d}}^{\prime }}\right) +\left( \ \fbox {$\hskip 1em $ $\mathrm {C}$ $\hskip 1em $} \ \right) \right] \cos \left( \omega t-\alpha \right) +i_{\mathrm {dc}} \\[ 5pt ] \end{eqnarray}$$ ここで，$\ T_{\mathrm {d}}^{\prime \prime } \ $：短絡初期過渡時定数，$\ T_{\mathrm {d}}^{\prime } \ $：短絡過渡時定数，
　　　　$\ \omega \ $：$\ 2\pi f\left( f \right. \ $は周波数$\ \left. \right) \ $，$\ t \ $：時間，$\ \alpha \ $：短絡瞬時の電圧の位相角，
　　　　$\ i_{\mathrm {dc}} \ $：過渡直流電流

上記の突発短絡相電流の交流分の振幅の$\ \mathrm {A} \ $，$\ \mathrm {B} \ $及び$\ \mathrm {C} \ $の式を直軸初期過渡リアクタンス$\ X_{\mathrm {d}}^{\prime \prime } \ $，直軸過渡リアクタンス$\ X_{\mathrm {d}}^{\prime } \ $，直軸同期リアクタンス$\ X_{\mathrm {d}} \ $及び短絡前の電機子相電圧（波高値）$\ E_{\mathrm {0}} \ $を用いて示しなさい。

(2)　突発短絡相電流$\ i_{\mathrm {ph}} \ $の交流分に関して，振幅の減衰曲線を振幅の第$\ 1 \ $項，第$\ 2 \ $項及び第$\ 3 \ $項の時間特性が判るように図で示しなさい。図を答案用紙に書き写して答えよ。さらに，直軸初期過渡リアクタンス$\ X_{\mathrm {d}}^{\prime \prime } \ $及び直軸過渡リアクタンス$\ X_{\mathrm {d}}^{\prime } \ $の算出式を$\ E_{\mathrm {0}} \ $，$\ \mathrm {A} \ $，$\ \mathrm {B} \ $及び$\ \mathrm {C} \ $を用いて示しなさい。

【ワンポイント解説】

非常に専門性の高い問題です。
同期機の専門書やJEC-2130等に記載がある内容ですが，電験のテキストには記載がない内容です。
ほとんどの受験生が選択しなかった内容と思いますので，参考程度として良い問題かと思います。

1.三相突発短絡試験による定数測定法
無負荷で電圧が発生している同期発電機の端子を三相突発短絡させた場合の突発短絡相電流$\ i_{\mathrm {ph}} \ $の波形は図1のようになり，最初は持続短絡電流よりも大きな突発短絡電流が流れ，時間の経過とともに減衰し，最終的には持続短絡電流が流れるようになります。
この波形を定量的に表すと，短絡前の電機子相電圧（波高値）$\ E_{\mathrm {0}} \ $，直軸初期過渡リアクタンス$\ X_{\mathrm {d}}^{\prime \prime } \ $，直軸過渡リアクタンス$\ X_{\mathrm {d}}^{\prime } \ $，直軸同期リアクタンス$\ X_{\mathrm {d}} \ $，短絡初期過渡時定数$\ T_{\mathrm {d}}^{\prime \prime } \ $，短絡過渡時定数$\ T_{\mathrm {d}}^{\prime } \ $，角周波数$\ \omega \ $，時間$\ t \ $，短絡瞬時の電圧の位相角$\ \alpha \ $，過渡直流電流$\ i_{\mathrm {dc}} \ $とすれば，
$$\begin{eqnarray} i_{\mathrm {ph}}&=&\left[ \left( \frac {E_{0}}{X_{\mathrm {d}}^{\prime \prime }}-\frac {E_{0}}{X_{\mathrm {d}}^{\prime }} \right) \mathrm {exp} \left( \frac {-t}{T_{\mathrm {d}}^{\prime \prime }}\right) +\left( \frac {E_{0}}{X_{\mathrm {d}}^{\prime }}-\frac {E_{0}}{X_{\mathrm {d}}} \right) \mathrm {exp} \left( \frac {-t}{T_{\mathrm {d}}^{\prime }}\right) +\left( \frac {E_{0}}{X_{\mathrm {d}}} \right) \right] \cos \left( \omega t-\alpha \right) +i_{\mathrm {dc}} \\[ 5pt ] \end{eqnarray}$$ となります。第一項の$\ \displaystyle \frac {E_{0}}{X_{\mathrm {d}}^{\prime \prime }}-\frac {E_{0}}{X_{\mathrm {d}}^{\prime }} \ $，第二項の$\ \displaystyle \frac {E_{0}}{X_{\mathrm {d}}^{\prime }}-\frac {E_{0}}{X_{\mathrm {d}}} \ $，第三項の$\ \displaystyle \frac {E_{0}}{X_{\mathrm {d}}} \ $がグラフのどの部分に対応するかを検討するとイメージがつきやすいです。

【解答】

(1)
突発短絡相電流$\ i_{\mathrm {ph}} \ $の交流分に関して，振幅の第$\ 1 \ $項，第$\ 2 \ $項に相当する部分は過渡交流分を表し，$\ T_{\mathrm {d}}^{\prime \prime }≪T_{\mathrm {d}}^{\prime } \ $であるから短絡瞬時の値は$\ X_{\mathrm {d}}^{\prime \prime } \ $によって制限され，時定数$\ T_{\mathrm {d}}^{\prime \prime } \ $で急速に減衰し，ついで，$\ X_{\mathrm {d}}^{\prime } \ $によって制限され，時定数$\ T_{\mathrm {d}}^{\prime } \ $で次第に減衰する。第$\ 3 \ $項に相当する部分は持続短絡電流で$\ X_{\mathrm {d}} \ $で制限され最後にこの値に落ちつく。したがって，突発短絡相電流$\ i_{\mathrm {ph}} \ $の交流分の振幅の$\ \mathrm {A} \ $，$\ \mathrm {B} \ $及び$\ \mathrm {C} \ $は次の式で表される。
$$\begin{eqnarray} \mathrm {A}&=&\displaystyle \frac {E_{0}}{X_{\mathrm {d}}^{\prime \prime }}-\frac {E_{0}}{X_{\mathrm {d}}^{\prime }} \\[ 5pt ] \mathrm {B}&=&\displaystyle \frac {E_{0}}{X_{\mathrm {d}}^{\prime }}-\frac {E_{0}}{X_{\mathrm {d}}} \\[ 5pt ] \mathrm {C}&=&\displaystyle \frac {E_{0}}{X_{\mathrm {d}}} \\[ 5pt ] \end{eqnarray}$$ (2)
突発短絡相電流$\ i_{\mathrm {ph}} \ $の交流分の振幅の減衰曲線を示す。

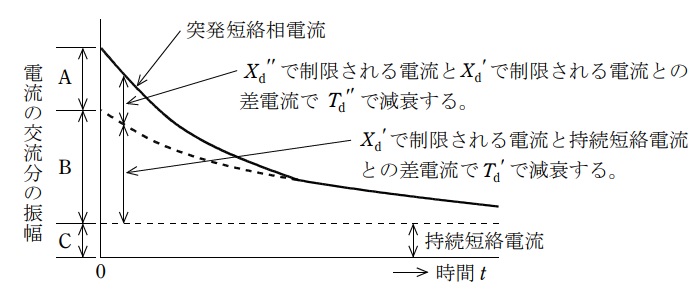
ワンポイント解説「1.三相突発短絡試験による定数測定法」の通り，
$$\begin{eqnarray} \frac {E_{0}}{X_{\mathrm {d}}^{\prime \prime }}&=&\mathrm {A}+\mathrm {B}+\mathrm {C} \\[ 5pt ] \frac {E_{0}}{X_{\mathrm {d}}^{\prime }}&=&\mathrm {B}+\mathrm {C} \\[ 5pt ] \frac {E_{0}}{X_{\mathrm {d}}}&=&\mathrm {C} \\[ 5pt ] \end{eqnarray}$$ であるから，それぞれ$\ X_{\mathrm {d}}^{\prime \prime } \ $，$\ X_{\mathrm {d}}^{\prime } \ $，$\ X_{\mathrm {d}} \ $について整理すると，
$$\begin{eqnarray} X_{\mathrm {d}}^{\prime \prime }&=&\frac {E_{0}}{\mathrm {A}+\mathrm {B}+\mathrm {C}} \\[ 5pt ] X_{\mathrm {d}}^{\prime }&=&\frac {E_{0}}{\mathrm {B}+\mathrm {C}} \\[ 5pt ] X_{\mathrm {d}}&=&\frac {E_{0}}{\mathrm {C}} \\[ 5pt ] \end{eqnarray}$$ と求められる。