《法規》〈電気施設管理〉[H28:問7] 特別高圧架空電線の想定荷重の計算方法に関する空欄穴埋問題

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，特別高圧架空電線の想定荷重の計算方法に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。

a　電線の張力計算に用いる想定荷重は，電線が\( \ \fbox {　 （１） 　} \ \)である場合を除き，水平荷重\( \ W_{\mathrm{W}} \ \mathrm { [ N/m ] } \ \)と垂直荷重\( \ W_{\mathrm{V}} \ \mathrm { [ N/m ] } \ \)の合成荷重\( \ W_{\mathrm{S}} \ \mathrm { [ N/m ] } \ \)を用いる。合成荷重\( \ W_{\mathrm{S}} \ \mathrm { [ N/m ] } \ \)は，次式で示される。
\[
W_{\mathrm{S}}=\fbox {　 （２） 　}
\] b　水平荷重\( \ W_{\mathrm{W}} \ \mathrm { [ N/m ] } \ \)としては風圧荷重をとる。甲種，乙種及び丙種の3種の風圧荷重があり，甲種風圧荷重を適用する場合，電線の垂直投影面に加わる風圧は，多導体では\( \ \fbox {　 （３） 　} \ \)による低減を考慮し単導体の\( \ 90 \ ％ \ \)として\( \ \fbox {　 （４） 　} \ \)\(\mathrm {Pa} \ \)をとる。ただし，多導体とは，構成する電線が2条ごとに水平に配列され，かつ，当該電線相互間の距離が電線の外径の\( \ 20 \ \)倍以下のものに限る。
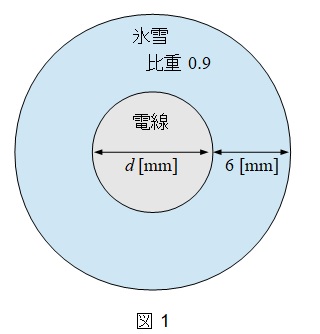
c　垂直荷重\( \ W_{\mathrm{V}} \ \mathrm { [ N/m ] } \ \)としては電線重量\( \ W_{\mathrm{C}} \ \mathrm { [ N/m ] } \ \)をとる。ただし，乙種風圧荷重を適用する場合は，外径\( \ d \ \mathrm { [ mm ] } \ \)の電線の周囲に厚さ\( \ 6 \ \mathrm { mm } \ \)，比重\( \ 0.9 \ \)の氷雪が付着した時の被氷重量も見込むものとし，この場合の垂直荷重\( \ W_{\mathrm{V}} \ \mathrm { [ N/m ] } \ \)は，次式で示される。
\[
W_{\mathrm{V}}=\fbox {　 （５） 　}
\]

〔問7の解答群〕
\[
\begin{eqnarray}
&（イ）&　W_{\mathrm{C}}+0.9\times \pi \times 6 \times \left( d+2\times 6\right) \times 10^{-3}\times 9.8　　　&（ロ）&　980 \\[ 5pt ] &（ハ）&　ケーブル　　　&（ニ）&　電線相互の干渉 \\[ 5pt ] &（ホ）&　W_{\mathrm{V}}+W_{\mathrm{W}}　　　&（ヘ）&　0.9\times \pi \times 6 \times \left( d^{2}+ 6\right) \times 10^{-3}\times 9.8 \\[ 5pt ] &（ト）&　銅　線　　　&（チ）&　構造規模の効果 \\[ 5pt ] &（リ）&　\frac {W_{\mathrm{V}}+W_{\mathrm{W}}}{2}　　　&（ヌ）&　\sqrt{W_{\mathrm{V}}^{2}+W_{\mathrm{W}}^{2}} \\[ 5pt ] &（ル）&　880　　　&（ヲ）&　風の収束 \\[ 5pt ] &（ワ）&　鋼　線　　　&（カ）&　1080 \\[ 5pt ] &（ヨ）&　W_{\mathrm{C}}+0.9\times \pi \times 6 \times \left( d+ 6\right) \times 10^{-3}\times 9.8
\end{eqnarray}
\]

【ワンポイント解説】

計算問題が易しいので，比較的点数の取りやすい問題であると思います。多導体以外の垂直投影面に加わる圧力\( \ 980 \ \mathrm {Pa} \ \)は覚えておきましょう。

【解答】

(1)解答：ハ
題意より，解答候補は（ハ）ケーブル，（ト）銅線，（ワ）鋼線となりますが，電線の張力計算はケーブルである場合を除き問題文aのような計算をします。

(2)解答：ヌ
水平荷重\( \ W_{\mathrm{W}} \ \mathrm { [ N/m ] } \ \)と垂直荷重\( \ W_{\mathrm{V}} \ \mathrm { [ N/m ] } \ \)の合成荷重は三平方の定理より，
\[
W_{\mathrm{S}}=\sqrt{W_{\mathrm{V}}^{2}+W_{\mathrm{W}}^{2}}
\] となります。

(3)解答：ニ
題意より，解答候補は（ニ）電線相互の干渉，（チ）構造規模の効果，（ヲ）風の収束となりますが，最も効果が高いと思われるのは（ニ）電線相互の干渉となります。

(4)解答：ル
多導体以外の垂直投影面に加わる圧力\( \ 980\mathrm {Pa} \ \)であり，多導体ではその90％となるので，
\[
980\times 0.9 ≒ 880 \ \mathrm { [ Pa ] }
\] となります。

(5)解答：ヨ
題意に沿って電線の断面のイメージを描くと図1のようになる。
図1において単位長さあたりの氷雪の体積\( \ V_{\mathrm{I}} \ \mathrm { [ m^{3} ] } \ \)は，
\[
\begin{eqnarray}
V_{\mathrm{I}}&=& \pi \cdot \left[ \left( \frac {d}{2}+6 \right) \times 10^{-3} \right]^{2}-\pi \cdot \left( \frac {d}{2}\times 10^{-3} \right) ^{2} \\[ 5pt ] &=&\pi \cdot \left( \frac {d^{2}}{4}+6d + 36\right) \times 10^{-6}-\pi \cdot \left( \frac {d}{2} \right) ^{2}\times 10^{-6} \\[ 5pt ] &=&\pi \cdot \left( 6d + 36\right) \times 10^{-6} \ \mathrm { [ m^{3} ] }
\end{eqnarray}
\] となるので，単位長さ当たりの氷雪荷重\( \ W_{\mathrm{I}} \ \mathrm { [ N/m ] } \ \)は，
\[
\begin{eqnarray}
W_{\mathrm{I}}&=&V_{\mathrm{I}}\times 0.9\times 10^{3} \times 9.8 \\[ 5pt ] &=&\pi \cdot \left( 6d + 36\right) \times 10^{-6}\times 0.9\times 10^{3} \times 9.8 \\[ 5pt ] &=&0.9\times \pi \times 6 \times \left( d+ 6\right) \times 10^{-3}\times 9.8 \ \mathrm { [ N/m ] }
\end{eqnarray}
\] と求められる。よって，垂直荷重\( \ W_{\mathrm{V}} \ \)は，電線重量\( \ W_{\mathrm{C}} \ \)と氷雪荷重\( \ W_{\mathrm{I}} \ \)の合計となるので，
\[
\begin{eqnarray}
W_{\mathrm{V}}&=&W_{\mathrm{C}}+W_{\mathrm{I}} \\[ 5pt ] &=&W_{\mathrm{C}}+0.9\times \pi \times 6 \times \left( d+ 6\right) \times 10^{-3}\times 9.8 \ \mathrm { [ N/m ] }
\end{eqnarray}
\] と求められる。