Contents
【問題】
【難易度】★★★☆☆(普通)
次の文章は,回路の過渡現象に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる式,数値又は図を解答群の中から選び,その記号をマークシートに記入しなさい。
図のように,抵抗\( \ R \ \),静電容量\( \ C \ \),電圧源\( \ E \ \)及びスイッチ\( \ \mathrm {S} \ \)を接続した回路がある。
時間\( \ t<0 \ \)においてスイッチ\( \ \mathrm {S} \ \)は\( \ \mathrm {a} \ \)側にあり,回路は定常状態であるとする。時刻\( \ t=0 \ \)においてスイッチ\( \ \mathrm {S} \ \)を\( \ \mathrm {a} \ \)側から\( \ \mathrm {b} \ \)側に切り替えた。時間\( \ t>0 \ \)における静電容量\( \ C \ \)の両端の電圧の時間的変化を表す式は,
\[
\begin{eqnarray}
v &=&E\times ( \ \fbox { (1) } \ – \ \fbox { (2) } \ ) ・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
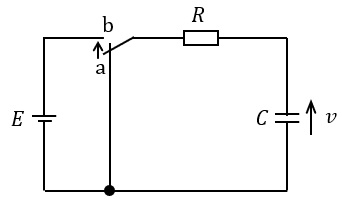
となり,その様子を表す図は\( \ \fbox { (3) } \ \)である。
\( \ v \ \)が\( \ \displaystyle \frac {2}{3}E \ \)となるまでの時間\( \ T \ \)は,
\[
\begin{eqnarray}
T &=& \ \fbox { (4) } \ ・・・・・・・・・・・・・・・・・・ ② \\[ 5pt ]
\end{eqnarray}
\]
である。静電容量\( \ C \ \)が\( \ C_{1} \ \),\( \ C_{2} \ \)の場合について時間\( \ T \ \)を測定すると,\( \ C_{1} \ \)のとき\( \ T=T_{1} \ \),\( \ C_{2} \ \)のとき\( \ T=T_{2} \ \)であった。したがって,
\[
\begin{eqnarray}
C_{2} &=&C_{1}\times \ \fbox { (5) } ・・・・・・・・・・・・・・・ ③ \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ C_{2} \ \)を\( \ C_{1} \ \),\( \ T_{1} \ \),\( \ T_{2} \ \)を用いて表すことができる。
〔問4の解答群〕
\[
\begin{eqnarray}
&(イ)& \mathrm {e}^{-\frac {t}{CR}} &(ロ)& CR \log_{\mathrm {e}}3 &(ハ)& \frac {T_{1}}{T_{2}} \\[ 5pt ]
&(ニ)& \mathrm {e}^{-CRt} &(ホ)& \frac {T_{2}}{T_{1}}\log_{\mathrm {e}}3 &(ヘ)& \frac {1}{3} \\[ 5pt ]
&(ト)& 0 &(チ)& \mathrm {e}^{\frac {t}{CR}} &(リ)& 1 \\[ 5pt ]
&(ヌ)& \frac {T_{2}}{T_{1}} &(ル)& \frac {1}{3}\mathrm {e}^{CR} &(ヲ)& \frac {1}{CR} \log_{\mathrm {e}}3 \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
\( \ RC \ \)直列回路の過渡現象に関する問題です。
\( \ 2 \ \)種の理論では,毎回のように出題される過渡現象ですが,微分方程式の解法はパターン化されていますので,ぜひ多くの問題を解いて慣れるようにして下さい。
1.過渡現象における\( \ RLC \ \)それぞれの電圧
過渡現象における\( \ RLC \ \)それぞれの電圧は,線路に流れる電流を\( \ i \ \)とし,抵抗\( \ R \ \)の電圧\( \ v_{\mathrm{R}} \ \),リアクトル\( \ L \ \)の電圧\( \ v_{\mathrm{L}} \ \),リアクトル\( \ C \ \)の電圧\( \ v_{\mathrm{C}} \ \)とすると,
\[
\begin{eqnarray}
v_{\mathrm{R}} &=& Ri \\[ 5pt ]
v_{\mathrm{L}} &=& L\frac {\mathrm {d}i}{\mathrm {d}t} \\[ 5pt ]
v_{\mathrm{C}} &=& \frac {1}{C}\int i \mathrm {d}t \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.過渡現象における定常解と過渡解
ⅰ.定常解を\( \ i_{\mathrm {s}} \ \),過渡解を\( \ i_{\mathrm {t}} \ \)とすると,一般解\( \ i \ \)は\( \ i=i_{\mathrm {s}}+i_{\mathrm {t}} \ \)となります。
ⅱ.定常解は電流の時間変化のない状態すなわち\( \ \displaystyle \frac {\mathrm {d}i_{\mathrm {s}}}{\mathrm {d}t}=0 \ \)とした時の解です。
ⅲ.過渡解はスイッチをオンまたはオフした直後の解で,直前の電圧や電流から変化する時の解です。
3.自然対数の微分積分
①自然対数の微分
\[
\begin{eqnarray}
\frac {\mathrm {d}}{\mathrm {d}x} \left( \ln {x}\right) &=&\frac {1}{x} \\[ 5pt ]
\end{eqnarray}
\]
②自然対数の積分
\[
\begin{eqnarray}
\int \frac {1}{x} \mathrm {d}x &=&\ln {x} + C \left( Cは積分定数\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,
\[
\begin{eqnarray}
\ln {x}&=&-\alpha t +C \left( Cは積分定数\right) \\[ 5pt ]
\end{eqnarray}
\]
となった場合,両辺とも対数を外すと,
\[
\begin{eqnarray}
x&=&A\mathrm {e}^{-\alpha t} \left( A=\mathrm {e}^{C}\right) \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)解答:リ
スイッチ\( \ \mathrm {S} \ \)を\( \ \mathrm {a} \ \)側から\( \ \mathrm {b} \ \)側に切り替えたときの回路方程式は,ワンポイント解説「1.過渡現象における\( \ RLC \ \)それぞれの電圧」の通り,
\[
\begin{eqnarray}
Ri+\frac {1}{C}\int i \mathrm {d}t&=&E \\[ 5pt ]
\end{eqnarray}
\]
であり,\( \ \displaystyle i=\frac {\mathrm {d}q}{\mathrm {d}t} \ \)の関係があるから,
\[
\begin{eqnarray}
R\frac {\mathrm {d}q}{\mathrm {d}t}+\frac {q}{C}&=&E \\[ 5pt ]
\end{eqnarray}
\]
となる。上式を\( \ E=0 \ \)として過渡解\( \ q_{\mathrm {t}} \ \)を求めると,ワンポイント解説「2.過渡現象における定常解と過渡解」及び「3.自然対数の微分積分」の通り,
\[
\begin{eqnarray}
R\frac {\mathrm {d}q_{\mathrm {t}}}{\mathrm {d}t}+\frac {q_{\mathrm {t}}}{C}&=&0 \\[ 5pt ]
R\frac {\mathrm {d}q_{\mathrm {t}}}{\mathrm {d}t}&=&-\frac {q_{\mathrm {t}}}{C} \\[ 5pt ]
\frac {1}{q_{\mathrm {t}}}\mathrm {d}q_{\mathrm {t}}&=&-\frac {1}{CR}\mathrm {d}t \\[ 5pt ]
\int \frac {1}{q_{\mathrm {t}}}\mathrm {d}q_{\mathrm {t}}&=&-\int \frac {1}{CR}\mathrm {d}t \\[ 5pt ]
\ln q_{\mathrm {t}}&=&- \frac {1}{CR}t + C^{\prime} \left( C^{\prime} \ は積分定数\right) \\[ 5pt ]
q_{\mathrm {t}}&=&A\mathrm {e}^{- \frac {1}{CR}t} \left( A=\mathrm {e}^{C^{\prime}} \right) \\[ 5pt ]
\end{eqnarray}
\]
となる。一方,\( \ \displaystyle \frac {\mathrm {d}q}{\mathrm {d}t}=0 \ \)として定常解\( \ q_{\mathrm {s}} \ \)を求めると,ワンポイント解説「2.過渡現象における定常解と過渡解」の通り,
\[
\begin{eqnarray}
\frac {q_{\mathrm {s}}}{C}&=&E \\[ 5pt ]
q_{\mathrm {s}}&=&CE \\[ 5pt ]
\end{eqnarray}
\]
となるので,一般解\( \ q \ \)は,
\[
\begin{eqnarray}
q&=&q_{\mathrm {s}}+q_{\mathrm {t}} \\[ 5pt ]
&=&CE+A\mathrm {e}^{- \frac {1}{CR}t} \\[ 5pt ]
\end{eqnarray}
\]
となる。\( \ t=0 \ \)において蓄えられる電荷\( \ q=0 \ \)であるから,
\[
\begin{eqnarray}
0&=&CE+A\mathrm {e}^{- \frac {1}{CR}\times 0} \\[ 5pt ]
0&=&CE+A \\[ 5pt ]
A&=&-CE \\[ 5pt ]
\end{eqnarray}
\]
となり,
\[
\begin{eqnarray}
q&=&CE-CE\mathrm {e}^{- \frac {1}{CR}t} \\[ 5pt ]
&=&CE\left( 1-\mathrm {e}^{- \frac {1}{CR}t}\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。\( \ q=Cv \ \)の関係から,
\[
\begin{eqnarray}
v&=&\frac {q}{C} \\[ 5pt ]
&=&\frac {CE\left( 1-\mathrm {e}^{- \frac {1}{CR}t}\right)}{C} \\[ 5pt ]
&=&E\left( 1-\mathrm {e}^{- \frac {1}{CR}t}\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,(1)は\( \ 1 \ \)と求められる。
(2)解答:イ
(1)解答式より,(2)は\( \ \mathrm {e}^{- \frac {1}{CR}t} \ \)と求められる。
(3)解答:ヨ
(1)解答式について,
\[
\begin{eqnarray}
v\left( 0\right)&=&E\left( 1-\mathrm {e}^{- \frac {1}{CR}\times 0}\right) \\[ 5pt ]
&=&E\left( 1-1\right) \\[ 5pt ]
&=&0 \\[ 5pt ]
v\left( \infty \right)&=&E\left( 1-\mathrm {e}^{- \frac {1}{CR}\times \infty}\right) \\[ 5pt ]
&=&E\left( 1-0\right) \\[ 5pt ]
&=&E \\[ 5pt ]
\end{eqnarray}
\]
であるから,これを満たす図は(ヨ)となる。
(4)解答:ロ
(1)解答式に,\( \ t=T \ \)及び\( \ \displaystyle v=\frac {2}{3}E \ \)を代入し,\( \ T \ \)について整理すると,
\[
\begin{eqnarray}
\frac {2}{3}E&=&E\left( 1-\mathrm {e}^{- \frac {1}{CR}T}\right) \\[ 5pt ]
\frac {2}{3}&=&1-\mathrm {e}^{- \frac {1}{CR}T} \\[ 5pt ]
\mathrm {e}^{- \frac {1}{CR}T}&=&\frac {1}{3} \\[ 5pt ]
– \frac {1}{CR}T&=&\log _{\mathrm {e}}\frac {1}{3} \\[ 5pt ]
&=&-\log _{\mathrm {e}}3 \\[ 5pt ]
\frac {1}{CR}T&=&\log _{\mathrm {e}}3 \\[ 5pt ]
T&=&CR\log _{\mathrm {e}}3 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ヌ
題意より,
\[
\begin{eqnarray}
T_{1}&=&C_{1}R\log _{\mathrm {e}}3 \\[ 5pt ]
T_{2}&=&C_{2}R\log _{\mathrm {e}}3 \\[ 5pt ]
\end{eqnarray}
\]
なので,第\( \ 1 \ \)式と第\( \ 2 \ \)式の比をとると,
\[
\begin{eqnarray}
\frac {T_{1}}{T_{2}}&=&\frac {C_{1}R\log _{\mathrm {e}}3}{C_{2}R\log _{\mathrm {e}} 3} \\[ 5pt ]
\frac {T_{1}}{T_{2}}&=&\frac {C_{1}}{C_{2}} \\[ 5pt ]
C_{2}&=&C_{1}\times \frac {T_{2}}{T_{1}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは