Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
次の文章は,電気回路の過渡現象に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
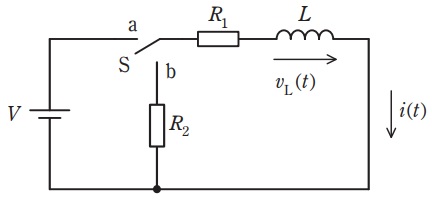
時刻\( \ t<0 \ \)では,図の回路のスイッチ\( \ \mathrm {S} \ \)は\( \ \mathrm {a} \ \)側にあり,回路は定常状態にある。この回路において,\( \ t=0 \ \)でスイッチ\( \ \mathrm {S} \ \)を\( \ \mathrm {b} \ \)側に切り替えるものとする。
図に示すように回路の電流を\( \ i\left( t \right) \ \)とすれば,\( \ t≧0 \ \)では,次式の回路方程式が成り立つ。
\[
\begin{eqnarray}
\ \fbox { (1) } \ &=&0 \\[ 5pt ]
\end{eqnarray}
\]
\( \ t=0 \ \)で\( \ i\left( 0 \right) = \ \fbox { (2) } \ \)であることに注意して,この回路方程式を解けば,
\[
\begin{eqnarray}
i\left( t \right) &=& \ \fbox { (3) } \ \\[ 5pt ]
\end{eqnarray}
\]
を得る。このとき時定数は\( \ \fbox { (4) } \ \)である。
また,\( \ t≧0 \ \)において,コイル\( \ L \ \)に発生する起電力\( \ v_{\mathrm {L}}\left( t \right) \ \)は次式で与えられる。
\[
\begin{eqnarray}
v_{\mathrm {L}}\left( t \right) &=&-L\frac {\mathrm {d}i\left( t \right) }{\mathrm {d}t}= \ \fbox { (5) } \ \\[ 5pt ]
\end{eqnarray}
\]
〔問5の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {R_{1}+R_{2}}{R_{1}}V\mathrm {e}^{-\left( \frac {R_{1}+R_{2}}{L}\right) t} &(ロ)& \frac {L}{R_{1}} &(ハ)& L\frac {\mathrm {d}i\left( t \right) }{\mathrm {d}t}+R_{1}i\left( t \right) \\[ 5pt ]
&(ニ)& \frac {R_{2}}{R_{1}}V\mathrm {e}^{-\left( \frac {R_{1}}{L}\right) t} &(ホ)& L\frac {\mathrm {d}i\left( t \right) }{\mathrm {d}t}+\left( R_{1}+R_{2}\right) i\left( t \right) &(ヘ)& \frac {L}{R_{1}+R_{2}} \\[ 5pt ]
&(ト)& L\frac {\mathrm {d}i\left( t \right) }{\mathrm {d}t}+R_{2}i\left( t \right) &(チ)& \frac {V}{R_{1}}\mathrm {e}^{-\left( \frac {L}{R_{1}+R_{2}}\right) t} &(リ)& \frac {R_{1}+R_{2}}{R_{1}}V\mathrm {e}^{-\left( \frac {L}{R_{1}+R_{2}}\right) t} \\[ 5pt ]
&(ヌ)& \frac {V}{R_{1}}\mathrm {e}^{-\left( \frac {R_{1}+R_{2}}{L}\right) t} &(ル)& \frac {R_{1}+R_{2}}{L} &(ヲ)& \frac {V}{R_{1}+R_{2}} \\[ 5pt ]
&(ワ)& \frac {V}{R_{1}+R_{2}}\mathrm {e}^{-\left( \frac {R_{1}}{L}\right) t} &(カ)& \frac {V}{R_{1}} &(ヨ)& \frac {V}{R_{2}} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
\( \ RL \ \)回路の過渡現象に関する問題です。
本問は例年の過渡現象の問題と比較すると幾分計算量は少なめの問題かと思います。
それぞれの素子がどのような働きをし,電流がどのようになるか,また微分積分の知識は必須となりますので,必ず理解するようにしましょう。
1.過渡現象における\( \ RLC \ \)それぞれの電圧
過渡現象における\( \ RLC \ \)それぞれの電圧は,線路に流れる電流を\( \ i \ \)とし,抵抗\( \ R \ \)の電圧\( \ v_{\mathrm{R}} \ \),リアクトル\( \ L \ \)の電圧\( \ v_{\mathrm{L}} \ \),リアクトル\( \ C \ \)の電圧\( \ v_{\mathrm{C}} \ \)とすると,
\[
\begin{eqnarray}
v_{\mathrm{R}} &=& Ri \\[ 5pt ]
v_{\mathrm{L}} &=& L\frac {\mathrm {d}i}{\mathrm {d}t} \\[ 5pt ]
v_{\mathrm{C}} &=& \frac {1}{C}\int i \mathrm {d}t \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.過渡現象における定常解と過渡解
ⅰ.定常解を\( \ i_{\mathrm {s}} \ \),過渡解を\( \ i_{\mathrm {t}} \ \)とすると,一般解\( \ i \ \)は\( \ i=i_{\mathrm {s}}+i_{\mathrm {t}} \ \)となります。
ⅱ.定常解は電流の時間変化のない状態すなわち\( \ \displaystyle \frac {\mathrm {d}i_{\mathrm {s}}}{\mathrm {d}t}=0 \ \)とした時の解です。
ⅲ.過渡解はスイッチをオンまたはオフした直後の解で,直前の電圧や電流から変化する時の解です。
3.自然対数の微分積分
①自然対数の微分
\[
\begin{eqnarray}
\frac {\mathrm {d}}{\mathrm {d}x} \left( \ln {x}\right) &=&\frac {1}{x} \\[ 5pt ]
\end{eqnarray}
\]
②自然対数の積分
\[
\begin{eqnarray}
\int \frac {1}{x} \mathrm {d}x &=&\ln {x} + C \left( Cは積分定数\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,
\[
\begin{eqnarray}
\ln {x}&=&-\alpha t +C \left( Cは積分定数\right) \\[ 5pt ]
\end{eqnarray}
\]
となった場合,両辺とも対数を外すと,
\[
\begin{eqnarray}
x&=&A\mathrm {e}^{-\alpha t} \left( A=\mathrm {e}^{C}\right) \\[ 5pt ]
\end{eqnarray}
\]
となります。
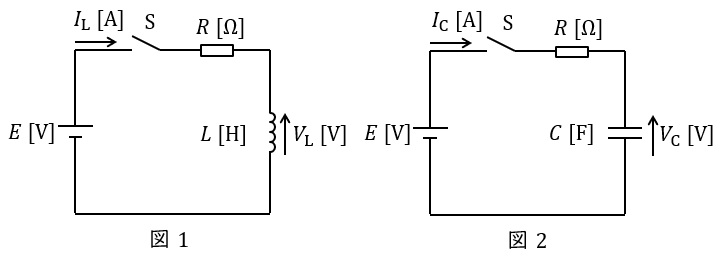
4.時定数
図1や図2のような回路が与えられるとき,図1のリアクトル電圧\( \ V_{\mathrm {L}} \ \mathrm {[V]} \ \)及び回路を流れる電流\( \ I_{\mathrm {L}} \ \mathrm {[A]} \ \),図2のコンデンサ電圧\( \ V_{\mathrm {C}} \ \mathrm {[V]} \ \)及び回路を流れる電流\( \ I_{\mathrm {C}} \ \mathrm {[A]} \ \)はそれぞれ,
\[
\begin{eqnarray}
V_{\mathrm {L}} &=&E\mathrm {e}^{-\frac {R}{L}t} \\[ 5pt ]
I_{\mathrm {L}} &=&\frac {E}{R}\left( 1-\mathrm {e}^{-\frac {R}{L}t}\right) \\[ 5pt ]
V_{\mathrm {C}} &=&E\left( 1-\mathrm {e}^{-\frac {t}{CR}}\right) \\[ 5pt ]
I_{\mathrm {C}} &=&\frac {E}{R}\mathrm {e}^{-\frac {t}{CR}} \\[ 5pt ]
\end{eqnarray}
\]
で求められ,上式の\( \ \mathrm {e} \ \)の指数が\( \ -1 \ \)(約\( \ 63.2 \ \mathrm {[%]} \ \)の変化)となる時間を時定数\( \ \tau \ \mathrm {[s]} \ \)と呼び\( \ \displaystyle \tau =\frac {L}{R} \ \)及び\( \ \tau =CR \ \)となります。
【解答】
(1)解答:ホ
スイッチ\( \ \mathrm {S} \ \)を\( \ \mathrm {b} \ \)側に切り替えたときの回路方程式は,
\[
\begin{eqnarray}
L\frac {\mathrm {d}i\left( t \right) }{\mathrm {d}t}+R_{1}i\left( t \right) +R_{2}i\left( t \right) &=&0 \\[ 5pt ]
L\frac {\mathrm {d}i\left( t \right) }{\mathrm {d}t}+\left( R_{1}+R_{2}\right) i\left( t \right) &=&0 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:カ
\( \ \mathrm {S} \ \)は\( \ \mathrm {a} \ \)側にあり,回路が定常状態であるときの電流が\( \ i\left( 0 \right) \ \)であるから,リアクトルは短絡と考えれば良いので,
\[
\begin{eqnarray}
i\left( 0 \right) &=&\frac {V}{R_{1}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ヌ
(1)解答式の微分方程式を解くと,
\[
\begin{eqnarray}
L\frac {\mathrm {d}i\left( t \right) }{\mathrm {d}t}+\left( R_{1}+R_{2}\right) i\left( t \right) &=&0 \\[ 5pt ]
L\frac {\mathrm {d}i\left( t \right) }{\mathrm {d}t}&=&-\left( R_{1}+R_{2}\right) i\left( t \right) \\[ 5pt ]
\frac {1}{i\left( t \right) }\mathrm {d}i\left( t \right) &=&-\frac {R_{1}+R_{2}}{L}\mathrm {d}t \\[ 5pt ]
\int \frac {1}{i\left( t \right) }\mathrm {d}i\left( t \right) &=&-\frac {R_{1}+R_{2}}{L}\int \mathrm {d}t \\[ 5pt ]
\ln i\left( t \right) &=&-\frac {R_{1}+R_{2}}{L}t+C \left( C \ は積分定数 \right) \\[ 5pt ]
i\left( t \right) &=&A\mathrm {e}^{-\left( \frac {R_{1}+R_{2}}{L}\right) t} \left( A \ は積分定数 \right) \\[ 5pt ]
\end{eqnarray}
\]
となり,(2)解答式より,\( \ \displaystyle i\left( 0 \right) =\frac {V}{R_{1}} \ \)であるから,
\[
\begin{eqnarray}
i\left( 0 \right) &=&A\mathrm {e}^{-\left( \frac {R_{1}+R_{2}}{L}\right) \times 0} \\[ 5pt ]
\frac {V}{R_{1}} &=&A \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
i\left( t \right) &=&\frac {V}{R_{1}}\mathrm {e}^{-\left( \frac {R_{1}+R_{2}}{L}\right) t} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ヘ
ワンポイント解説「4.時定数」の通り,時定数\( \ \displaystyle \tau =\frac {L}{R_{1}+R_{2}} \ \)と求められる。
(5)解答:イ
題意より,
\[
\begin{eqnarray}
v_{\mathrm {L}}\left( t \right) &=&-L\frac {\mathrm {d}i\left( t \right) }{\mathrm {d}t}=-L\frac {\mathrm {d}}{\mathrm {d}t}\left\{ \frac {V}{R_{1}}\mathrm {e}^{-\left( \frac {R_{1}+R_{2}}{L}\right) t}\right\} \\[ 5pt ]
\end{eqnarray}
\]
であるから,\( \ \displaystyle X= -\left( \frac {R_{1}+R_{2}}{L}\right) t \ \)とおくと,\( \ \displaystyle i\left( X \right) =\frac {V}{R_{1}}\mathrm {e}^{X} \ \)となるので,
\[
\begin{eqnarray}
v_{\mathrm {L}}\left( t \right) &=&-L\frac {\mathrm {d}i\left( t \right) }{\mathrm {d}t} \\[ 5pt ]
&=&-L\frac {\mathrm {d}X}{\mathrm {d}t}\cdot \frac {\mathrm {d}i\left( X \right) }{\mathrm {d}X} \\[ 5pt ]
&=&-L\left( -\frac {R_{1}+R_{2}}{L}\right)\cdot \frac {V}{R_{1}}\mathrm {e}^{X} \\[ 5pt ]
&=&\frac {R_{1}+R_{2}}{R_{1}}V\mathrm {e}^{-\left( \frac {R_{1}+R_{2}}{L}\right) t} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは