Contents
【問題】
【難易度】★★★☆☆(普通)
配電線のループ系統に関して,次の問に答えよ。
異なる配電用変圧器に接続されているこう長\( \ 1 \ \mathrm {km} \ \)の三相高圧配電線\( \ \mathrm {A} \ \)と\( \ \mathrm {B} \ \)の末端に開閉器が設置されている。開閉器を投入しループ系統にした場合,下記(1)~(3)の設問に答えよ。
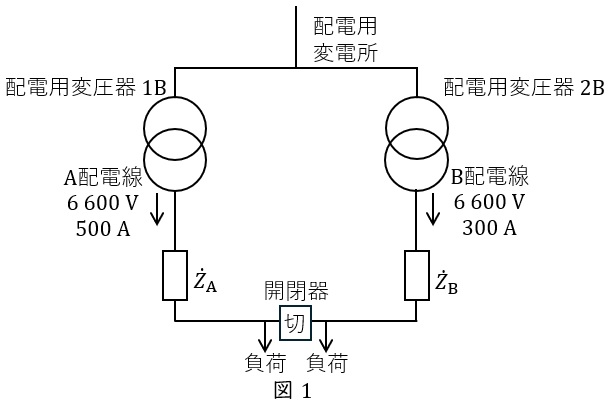
(1) 図1の系統において,開閉器投入後の\( \ \mathrm {A} \ \)配電線と\( \ \mathrm {B} \ \)配電線の送り出し電流の大きさを求めよ。
なお,配電用変電所から末端負荷に向かう電流の向きを正とする。
また,配電系統の条件を下記に示す。
・配電用変圧器\( \ \left( \mathrm {1B,2B} \right) \ \)の送り出し電圧は,\( \ 6 \ 600 \ \mathrm {V} \ \)とする。
・配電用変圧器の送り出し電圧は,開閉器投入前後で変化しない。
・配電用変圧器\( \ \left( \mathrm {1B,2B} \right) \ \)のインピーダンスは,無視できる。
・開閉器投入前の\( \ \mathrm {A} \ \)配電線,\( \ \mathrm {B} \ \)配電線の送り出しのそれぞれの電圧と電流の位相差は小さく,零としてよい。
・負荷は全てそれぞれの配電線の末端に接続されている。
・負荷電流は,開閉器投入前後で変化しない。
・\( \ \mathrm {A} \ \)配電線のインピーダンス:\( \ {\dot Z}_{\mathrm {A}} \ \mathrm {[\Omega / km]} \ \),\( \ \mathrm {B} \ \)配電線のインピーダンス:\( \ {\dot Z}_{\mathrm {B}} \ \mathrm {[\Omega / km]} \ \),\( \ {\dot Z}_{\mathrm {A}}={\dot Z}_{\mathrm {B}}={\dot Z} \ \mathrm {[\Omega / km]} \ \)
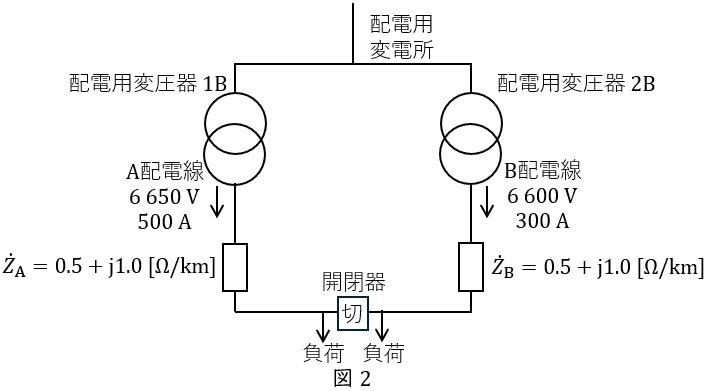
(2) 小問(1)において,図2の系統のように送り出し電圧が異なる場合,開閉器投入後の\( \ \mathrm {A} \ \)配電線と\( \ \mathrm {B} \ \)配電線の送り出し電流の大きさを求めよ。
なお,小問(1)からの配電系統の条件の違いを下記に示す。
・配電用変圧器\( \ \left( \mathrm {1B,2B} \right) \ \)の送り出し電圧は,\( \ \mathrm {1B}:6 \ 650 \ \mathrm {V} \ \),\( \ \mathrm {2B}:6 \ 600 \ \mathrm {V} \ \)とする。
・\( \ {\dot Z}_{\mathrm {A}}={\dot Z}_{\mathrm {B}}={\dot Z}=0.5+\mathrm {j}1.0 \ \mathrm {[\Omega / km]} \ \)
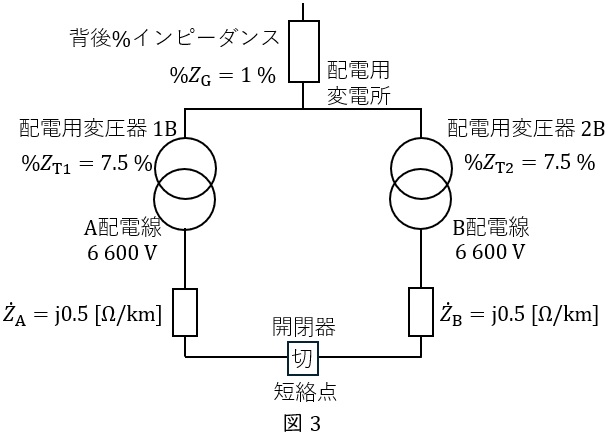
(3) 図3の系統において,開閉器投入後の三相短絡電流を求めよ。なお,短絡箇所は開閉器とする。
また,配電系統の条件を下記に示す。
・配電用変圧器\( \ \left( \mathrm {1B,2B} \right) \ \)の送り出し電圧は,\( \ 6 \ 600 \ \mathrm {V} \ \)とする。
・基準容量:\( \ 6 \ 600 \ \mathrm {V} \ \),\( \ 10 \ \mathrm {MV\cdot A} \ \)ベース
・背後%インピーダンス(抵抗成分は無視):\( \ %Z_{\mathrm {G}} =1 \ \mathrm {%} \ \)
・配電用変圧器%インピーダンス(抵抗成分は無視):\( \ %Z_{\mathrm {T1}}=%Z_{\mathrm {T2}}=%Z_{\mathrm {T}}=7.5 \ \mathrm {%} \ \)
・\( \ {\dot Z}_{\mathrm {A}}={\dot Z}_{\mathrm {B}}={\dot Z}=\mathrm {j}0.5 \ \mathrm {[\Omega / km]} \ \)(抵抗成分は無視)
【ワンポイント解説】
連系開閉器で接続される配電線のループ系統に関する問題です。
考え方は易しめですが,高い計算力を必要とする問題です。
電験の二次試験では,複素数を含むことでかなり計算量が多くなる問題があります。計算間違いに注意して丁寧に解き,確実に得点できるようにしましょう。
1.ループ配電系統の考え方
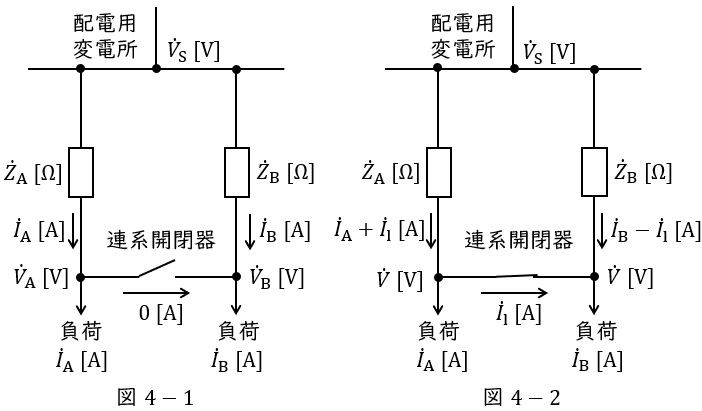
図4-1及び図4-2に示すように,配電用変電所の同一バンクから異なる配電線で供給され,連系開閉器で接続されているループ配電系統について考えます。連系開閉器投入前の状態が図4-1の通りであるとすると,連系開閉器投入前の各電圧の関係は,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {A}} &=&{\dot V}_{\mathrm {S}}-{\dot Z}_{\mathrm {A}}{\dot I}_{\mathrm {A}} \\[ 5pt ]
{\dot V}_{\mathrm {B}} &=&{\dot V}_{\mathrm {S}}-{\dot Z}_{\mathrm {B}}{\dot I}_{\mathrm {B}} \\[ 5pt ]
\end{eqnarray}
\]
であり,\( \ {\dot V}_{\mathrm {A}}≠{\dot V}_{\mathrm {B}} \ \)のとき,連系開閉器を投入すると電圧\( \ {\dot V}_{\mathrm {A}} \ \)と\( \ {\dot V}_{\mathrm {B}} \ \)が等しくなるようにループ電流が流れます。
このときの電圧を\( \ {\dot V} \ \mathrm {[V]} \ \),\( \ \mathrm {A} \ \)から\( \ \mathrm {B} \ \)に向かうループ電流が\( \ {\dot I}_{\mathrm {l}} \ \mathrm {[A]} \ \)であるとすると,配電系統全体では図4-2に示すように変化し,
\[
\begin{eqnarray}
\dot V &=&{\dot V}_{\mathrm {S}}-{\dot Z}_{\mathrm {A}}\left( {\dot I}_{\mathrm {A}}+{\dot I}_{\mathrm {l}}\right) \\[ 5pt ]
\dot V &=&{\dot V}_{\mathrm {S}}-{\dot Z}_{\mathrm {B}}\left( {\dot I}_{\mathrm {B}}-{\dot I}_{\mathrm {l}}\right) \\[ 5pt ]
\end{eqnarray}
\]
すなわち,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {S}}-{\dot Z}_{\mathrm {A}}\left( {\dot I}_{\mathrm {A}}+{\dot I}_{\mathrm {l}}\right) &=&{\dot V}_{\mathrm {S}}-{\dot Z}_{\mathrm {B}}\left( {\dot I}_{\mathrm {B}}-{\dot I}_{\mathrm {l}}\right) \\[ 5pt ]
{\dot Z}_{\mathrm {A}}\left( {\dot I}_{\mathrm {A}}+{\dot I}_{\mathrm {l}}\right) &=&{\dot Z}_{\mathrm {B}}\left( {\dot I}_{\mathrm {B}}-{\dot I}_{\mathrm {l}}\right) \\[ 5pt ]
\end{eqnarray}
\]
が成立します。
2.オーム法から百分率インピーダンス法への変換
基準容量を\( \ P_{\mathrm {n}} \ \mathrm {[V\cdot A]} \ \),基準電圧を\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \),基準電流を\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)とすると,
\[
\begin{eqnarray}
%Z&=&\frac {ZI_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}\times 100 (定義) \\[ 5pt ]
&=&\frac {\sqrt {3}ZI_{\mathrm {n}}}{V_{\mathrm {n}}}\times 100 \\[ 5pt ]
&=&\frac {\sqrt {3}ZV_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}}\times 100 \\[ 5pt ]
&=&\frac {P_{\mathrm {n}}Z}{V_{\mathrm {n}}^{2}}\times 100 (∵P_{\mathrm {n}}=\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} ) \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.百分率インピーダンスの短絡電流計算
百分率インピーダンスを\( \ %Z \ \mathrm {[%]} \ \)とすると,三相短絡電流\( \ I_{\mathrm {s}} \ \mathrm {[A]} \ \)は,基準電流\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)を用いて,
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {I_{\mathrm {n}}}{%Z/100} \\[ 5pt ]
&=&\frac {100I_{\mathrm {n}}}{%Z} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
※百分率インピーダンスの定義式等を用いて\( \ \displaystyle I_{\mathrm {s}}=\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}} \ \)から上式を求めることはできますが,試験時には暗記しておいた方が良いと思います。
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}{Z_{\mathrm {s}} \ \mathrm {[\Omega ]}} \\[ 5pt ]
&=&\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}} \\[ 5pt ]
&=&\frac {V_{\mathrm {n}}I_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}I_{\mathrm {n}}} \\[ 5pt ]
&=&\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}I_{\mathrm {n}}}\times I_{\mathrm {n}} \\[ 5pt ]
&=&\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}I_{\mathrm {n}}\times 100}\times 100I_{\mathrm {n}} \\[ 5pt ]
&=&\frac {100I_{\mathrm {n}}}{%Z_{\mathrm {s}}} \\[ 5pt ]
\end{eqnarray}
\]
【解答】
(1)図1の系統において,開閉器投入後の\( \ \mathrm {A} \ \)配電線と\( \ \mathrm {B} \ \)配電線の送り出し電流の大きさ
ワンポイント解説「1.ループ配電系統の考え方」の通り,開閉器投入後は\( \ {\dot Z}_{\mathrm {A}} \ \)及び\( \ {\dot Z}_{\mathrm {B}} \ \)での電圧降下が等しくなり,問題の条件より\( \ {\dot Z}_{\mathrm {A}}={\dot Z}_{\mathrm {B}}=\dot Z \ \)なので,各配電線を流れる電流の大きさは等しくなる。
したがって,各配電線の送り出し電流\( \ I_{\mathrm {A}} \ \mathrm {[A]} \ \)及び\( \ I_{\mathrm {B}} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {A}}=I_{\mathrm {B}} &=&\frac {500+300}{2} \\[ 5pt ]
&=&400 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
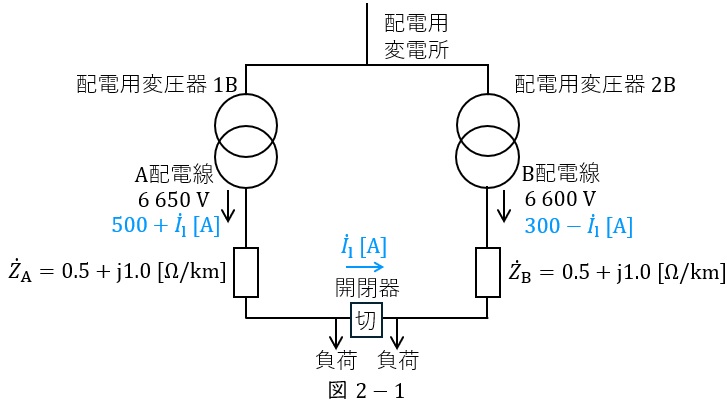
(2)図2における開閉器投入後の\( \ \mathrm {A} \ \)配電線と\( \ \mathrm {B} \ \)配電線の送り出し電流の大きさ
開閉器投入後の状態を図2-1に示す。
ワンポイント解説「1.ループ配電系統の考え方」の通り,開閉器投入後各配電線の電圧は等しくなるから,
\[
\begin{eqnarray}
\frac {6 \ 650}{\sqrt {3}}-{\dot Z}_{\mathrm {A}}\left( 500+{\dot I}_{\mathrm {l}}\right) &=&\frac {6 \ 600}{\sqrt {3}}-{\dot Z}_{\mathrm {B}}\left( 300-{\dot I}_{\mathrm {l}}\right) \\[ 5pt ]
\frac {6 \ 650}{\sqrt {3}}-\left( 0.5+\mathrm {j}1.0 \right) \left( 500+{\dot I}_{\mathrm {l}}\right) &=&\frac {6 \ 600}{\sqrt {3}}-\left( 0.5+\mathrm {j}1.0\right) \left( 300- {\dot I}_{\mathrm {l}} \right) \\[ 5pt ]
\left( 0.5+\mathrm {j}1.0\right) \left( 500+{\dot I}_{\mathrm {l}}\right)-\left( 0.5+\mathrm {j}1.0\right) \left( 300-{\dot I}_{\mathrm {l}}\right) &=&\frac {6 \ 650}{\sqrt {3}}-\frac {6 \ 600}{\sqrt {3}} \\[ 5pt ]
\left( 0.5+\mathrm {j}1.0\right) \left\{ \left( 500+{\dot I}_{\mathrm {l}}\right)- \left( 300-{\dot I}_{\mathrm {l}}\right) \right\} &=&\frac {50}{\sqrt {3}} \\[ 5pt ]
\left( 0.5+\mathrm {j}1.0\right) \left( 200+2{\dot I}_{\mathrm {l}}\right) &≒&28.868 \\[ 5pt ]
200+2{\dot I}_{\mathrm {l}} &=&\frac {28.868}{0.5+\mathrm {j}1.0} \\[ 5pt ]
&=&\frac {28.868}{0.5+\mathrm {j}1.0}\times \frac {0.5-\mathrm {j}1.0}{0.5-\mathrm {j}1.0} \\[ 5pt ]
&=&\frac {14.434-\mathrm {j}28.868}{0.25+1.0} \\[ 5pt ]
&≒&11.547-\mathrm {j}23.094 \\[ 5pt ]
2{\dot I}_{\mathrm {l}} &=&-200+\left(11.547-\mathrm {j}23.094\right) \\[ 5pt ]
&≒&-188.45-\mathrm {j}23.094 \\[ 5pt ]
{\dot I}_{\mathrm {l}}&=&-94.225-\mathrm {j}11.547 \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,各配電線の送り出し電流\( \ {{\dot I}_{\mathrm {A}}}^{\prime } \ \mathrm {[A]} \ \)及び\( \ {{\dot I}_{\mathrm {B}}}^{\prime } \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
{{\dot I}_{\mathrm {A}}}^{\prime } &=&500+{\dot I}_{\mathrm {l}} \\[ 5pt ]
&=&500-94.225-\mathrm {j}11.547 \\[ 5pt ]
&≒&405.78-\mathrm {j}11.547 \\[ 5pt ]
{{\dot I}_{\mathrm {B}}}^{\prime } &=&300-{\dot I}_{\mathrm {l}} \\[ 5pt ]
&=&300-\left( -94.225-\mathrm {j}11.547\right) \\[ 5pt ]
&≒&394.23+\mathrm {j}11.547 \\[ 5pt ]
\end{eqnarray}
\]
となるので,その大きさ\( \ {I_{\mathrm {A}}}^{\prime } \ \mathrm {[A]} \ \)及び\( \ {I_{\mathrm {B}}}^{\prime } \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
{I_{\mathrm {A}}}^{\prime } &=&\sqrt {405.78^{2}+11.547^{2}} \\[ 5pt ]
&≒&405.94 → 406 \ \mathrm {[A]} \\[ 5pt ]
{I_{\mathrm {B}}}^{\prime } &=&\sqrt {394.23^{2}+11.547^{2}} \\[ 5pt ]
&≒&394.40 → 394 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)図3の系統における開閉器投入後の三相短絡電流
配電線の百分率インピーダンス\( \ %Z_{\mathrm {A}}=%Z_{\mathrm {B}}=%Z \ \mathrm {[%]} \ \)は,長さが\( \ 1 \ \mathrm {km} \ \)であるから,ワンポイント解説「2.オーム法から百分率インピーダンス法への変換」の通り,
\[
\begin{eqnarray}
%Z &=&\frac {P_{\mathrm {n}}Z}{V_{\mathrm {n}}^{2}}\times 100 \\[ 5pt ]
&=&\frac {10\times 10^{6}\times 0.5}{6 \ 600^{2}}\times 100 \\[ 5pt ]
&≒&11.478 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,短絡点からみた百分率インピーダンス\( \ %Z_{\mathrm {s}} \ \mathrm {[%]} \ \)は,
\[
\begin{eqnarray}
%Z_{\mathrm {s}} &=&%Z_{\mathrm {G}}+\frac {\left( %Z_{\mathrm {T1}}+%Z_{\mathrm {A}}\right) \left( %Z_{\mathrm {T2}}+%Z_{\mathrm {B}}\right) }{\left( %Z_{\mathrm {T1}}+%Z_{\mathrm {A}}\right) +\left( %Z_{\mathrm {T2}}+%Z_{\mathrm {B}}\right) } \\[ 5pt ]
&=&%Z_{\mathrm {G}}+\frac {\left( %Z_{\mathrm {T}}+%Z\right) \left( %Z_{\mathrm {T}}+%Z\right) }{2\left( %Z_{\mathrm {T}}+%Z\right) } \\[ 5pt ]
&=&%Z_{\mathrm {G}}+\frac {%Z_{\mathrm {T}}+%Z}{2} \\[ 5pt ]
&=&1+\frac {7.5+11.478}{2} \\[ 5pt ]
&=&10.489 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
となる。また,基準電流\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {n}} &=&\frac {P_{\mathrm {n}}}{\sqrt {3}V_{\mathrm {n}}} \\[ 5pt ]
&=&\frac {10\times 10^{6}}{\sqrt {3}\times 6 \ 600} \\[ 5pt ]
&≒&874.77 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
なので,三相短絡電流\( \ I_{\mathrm {s}} \ \mathrm {[A]} \ \)は,ワンポイント解説「3.百分率インピーダンスの短絡電流計算」の通り,
\[
\begin{eqnarray}
I_{\mathrm {s}} &=&\frac {100I_{\mathrm {n}}}{%Z_{\mathrm {s}}} \\[ 5pt ]
&=&\frac {100\times 874.77}{10.489} \\[ 5pt ]
&≒&8 \ 339.9 → 8 \ 340 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは