Contents
【問題】
【難易度】★★★☆☆(普通)
次の文章は,回路の過渡現象に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる式又は数値を解答群の中から選び,その記号をマークシートに記入しなさい。
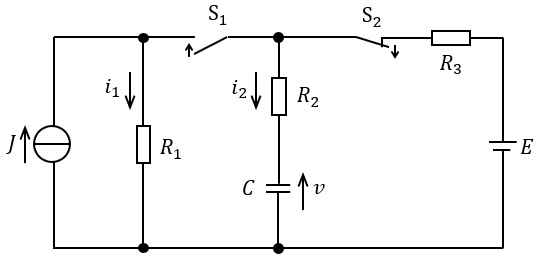
図のように,抵抗\( \ R_{1} \ \),\( \ R_{2} \ \),\( \ R_{3} \ \),静電容量\( \ C \ \)及び電圧源\( \ E \ \),電流源\( \ J \ \)を接続した回路がある。
スイッチを次のように開閉したとき,抵抗\( \ R_{1} \ \),\( \ R_{2} \ \)に流れる電流\( \ i_{1} \ \),\( \ i_{2} \ \)と静電容量\( \ C \ \)の両端の電圧\( \ v \ \)の時間的変化を求めたい。
時間\( \ t < 0 \ \)ではスイッチ\( \ \mathrm {S_{1}} \ \)は開いた状態,スイッチ\( \ \mathrm {S_{2}} \ \)は閉じた状態にあり,回路は定常状態であるとする。このとき\( \ v \ \)は\( \ \fbox { (1) } \ \)である。
時刻\( \ t = 0 \ \)において,スイッチ\( \ \mathrm {S_{1}} \ \)を閉じると同時にスイッチ\( \ \mathrm {S_{2}} \ \)を開いた。この状態での時間\( \ t > 0 \ \)における電流\( \ i_{1} \ \),\( \ i_{2} \ \)の時間的変化を求めることを考える。電圧,電流の時間的変化を求める回路方程式は次式となる。
\[
\begin{eqnarray}
J &=&i_{1}+i_{2} & \ ・・・・・・・・・・・・・・・・・・・・・・・ ①& \\[ 5pt ]
R_{1}i_{1}&=&R_{2}i_{2}+v & \ ・・・・・・・・・・・・・・・・・・・・・・・ ②& \\[ 5pt ]
i_{2}&=&C\frac {\mathrm {d}v}{\mathrm {d}t} & \ ・・・・・・・・・・・・・・・・・・・・・・・ ③& \\[ 5pt ]
\end{eqnarray}
\]
これらの式より電圧\( \ v \ \)に関する微分方程式が得られる。この式を初期条件を考慮して解くと,\( \ v \ \)は次式で表される。
\[
\begin{eqnarray}
v &=& \ \fbox { (1) } \ \times \mathrm {e}^{ \ \fbox { (2) } \ \times t}+ \ \fbox { (3) } \ \times \left( 1-\mathrm {e}^{ \ \fbox { (2) } \ \times t} \right) &・・・ ④& \\[ 5pt ]
\end{eqnarray}
\]
①〜④式より\( \ i_{1} \ \),\( \ i_{2} \ \)を求めることができ,特に定常状態においては\( \ i_{1} \ \)は\( \ \fbox { (4) }\times J \ \), \( \ i_{2} \ \)は\( \ \fbox { (5) }\times J \ \)となる。
〔問4の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {R_{3}}{R_{2}+R_{3}}E &(ロ)& \frac {R_{2}}{R_{1}+R_{2}} &(ハ)& E \\[ 5pt ]
&(ニ)& -\frac {1}{C\left( R_{1}+R_{2}\right) } &(ホ)& \left( \frac {1}{R_{1}}+\frac {1}{R_{2}}\right) J &(ヘ)& \frac {R_{1}}{R_{2}} \\[ 5pt ]
&(ト)& -\frac {\left( R_{1}+R_{2}\right) }{C} &(チ)& 0 &(リ)& \left( R_{1}+R_{2}\right) J \\[ 5pt ]
&(ヌ)& \frac {R_{2}}{R_{1}} &(ル)& R_{1}J &(ヲ)& \frac {R_{1}}{R_{1}+R_{2}} \\[ 5pt ]
&(ワ)& -\frac {C}{R_{1}+R_{2}} &(カ)& \frac {R_{2}}{R_{2}+R_{3}}E &(ヨ)& 1 \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
電源に電圧源と電流源を持つ\( \ RC \ \)直並列回路の過渡現象に関する問題です。
本問は電流ではなく電圧の微分方程式なので例年と少し異なりますが,過渡現象に関する微分方程式の計算は\( \ 2 \ \)種では必須の内容となります。
慣れてしまえば得点源となり得る分野ですので,しっかりと解法を理解するようにしましょう。
1.過渡現象における\( \ RLC \ \)それぞれの電圧
過渡現象における\( \ RLC \ \)それぞれの電圧は,線路に流れる電流を\( \ i \ \)とし,抵抗\( \ R \ \)の電圧\( \ v_{\mathrm{R}} \ \),リアクトル\( \ L \ \)の電圧\( \ v_{\mathrm{L}} \ \),リアクトル\( \ C \ \)の電圧\( \ v_{\mathrm{C}} \ \)とすると,
\[
\begin{eqnarray}
v_{\mathrm{R}} &=& Ri \\[ 5pt ]
v_{\mathrm{L}} &=& L\frac {\mathrm {d}i}{\mathrm {d}t} \\[ 5pt ]
v_{\mathrm{C}} &=& \frac {1}{C}\int i \mathrm {d}t \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.過渡現象における定常解と過渡解
ⅰ.定常解を\( \ i_{\mathrm {s}} \ \),過渡解を\( \ i_{\mathrm {t}} \ \)とすると,一般解\( \ i \ \)は\( \ i=i_{\mathrm {s}}+i_{\mathrm {t}} \ \)となります。
ⅱ.定常解は電流の時間変化のない状態すなわち\( \ \displaystyle \frac {\mathrm {d}i_{\mathrm {s}}}{\mathrm {d}t}=0 \ \)とした時の解です。
ⅲ.過渡解はスイッチをオンまたはオフした直後の解で,直前の電圧や電流から変化する時の解です。
3.自然対数の微分積分
①自然対数の微分
\[
\begin{eqnarray}
\frac {\mathrm {d}}{\mathrm {d}x} \left( \ln {x}\right) &=&\frac {1}{x} \\[ 5pt ]
\end{eqnarray}
\]
②自然対数の積分
\[
\begin{eqnarray}
\int \frac {1}{x} \mathrm {d}x &=&\ln {x} + C \left( Cは積分定数\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,
\[
\begin{eqnarray}
\ln {x}&=&-\alpha t +C \left( Cは積分定数\right) \\[ 5pt ]
\end{eqnarray}
\]
となった場合,両辺とも対数を外すと,
\[
\begin{eqnarray}
x&=&A\mathrm {e}^{-\alpha t} \left( A=\mathrm {e}^{C}\right) \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)解答:ハ
\( \ t < 0 \ \)においては,定常状態であるため,コンデンサ\( \ C \ \)は充電され電流を流さない。
したがって,電源電圧\( \ E \ \)は全てコンデンサ\( \ C \ \)に加わるため,\( \ v \left( 0\right) =E \ \)と求められる。
(2)解答:ニ
①式より,
\[
\begin{eqnarray}
i_{1} &=&J-i_{2} \\[ 5pt ]
\end{eqnarray}
\]
であるため,これを②式に代入すると,
\[
\begin{eqnarray}
R_{1}\left( J-i_{2}\right) &=&R_{2}i_{2}+v \\[ 5pt ]
R_{1}J-R_{1}i_{2} &=&R_{2}i_{2}+v \\[ 5pt ]
\left( R_{1}+R_{2}\right) i_{2} &=&R_{1}J-v \\[ 5pt ]
\end{eqnarray}
\]
となるので,これに③式を代入すれば,
\[
\begin{eqnarray}
\left( R_{1}+R_{2}\right) C\frac {\mathrm {d}v}{\mathrm {d}t} &=&R_{1}J-v \\[ 5pt ]
\left( R_{1}+R_{2}\right) C\frac {\mathrm {d}v}{\mathrm {d}t} +v&=&R_{1}J \\[ 5pt ]
\end{eqnarray}
\]
となる。この微分方程式の過渡解を\( \ v_{t} \ \)とすれば,
\[
\begin{eqnarray}
\left( R_{1}+R_{2}\right) C\frac {\mathrm {d}v_{t}}{\mathrm {d}t} +v_{t}&=&0 \\[ 5pt ]
\left( R_{1}+R_{2}\right) C\frac {\mathrm {d}v_{t}}{\mathrm {d}t} &=&-v_{t} \\[ 5pt ]
\frac {1}{v_{t}}\mathrm {d}v_{t} &=&-\frac {1}{\left( R_{1}+R_{2}\right)C}\mathrm {d}t \\[ 5pt ]
\end{eqnarray}
\]
と変数分離でき,両辺積分すると,ワンポイント解説「3.自然対数の微分積分」の通り,
\[
\begin{eqnarray}
\int \frac {1}{v_{t}}\mathrm {d}v_{t} &=&-\int \frac {1}{\left( R_{1}+R_{2}\right)C}\mathrm {d}t \\[ 5pt ]
\ln v_{t}&=&-\frac {1}{\left( R_{1}+R_{2}\right)C}t+C^{\prime } \left( C^{\prime } \ は積分定数\right) \\[ 5pt ]
v_{t}&=&A\mathrm {e}^{-\frac {1}{\left( R_{1}+R_{2}\right)C}t} \left( A \ は積分定数\right) \\[ 5pt ]
\end{eqnarray}
\]
となる。一方,微分方程式の定常解を\( \ v_{s} \ \)とすれば,
\[
\begin{eqnarray}
v_{s}&=&R_{1}J \\[ 5pt ]
\end{eqnarray}
\]
となるので,一般解\( \ v \ \)は,ワンポイント解説「2.過渡現象における定常解と過渡解」の通り,
\[
\begin{eqnarray}
v&=&v_{s}+v_{t} \\[ 5pt ]
&=&R_{1}J+A\mathrm {e}^{-\frac {1}{\left( R_{1}+R_{2}\right)C}t} \\[ 5pt ]
\end{eqnarray}
\]
となる。(1)解答式より,初期条件\( \ v \left( 0\right) =E \ \)であるため,
\[
\begin{eqnarray}
E&=&R_{1}J+A \\[ 5pt ]
A&=&E-R_{1}J \\[ 5pt ]
\end{eqnarray}
\]
となり,
\[
\begin{eqnarray}
v&=&v_{s}+v_{t} \\[ 5pt ]
&=&R_{1}J+\left( E-R_{1}J\right)\mathrm {e}^{-\frac {1}{\left( R_{1}+R_{2}\right)C}t} \\[ 5pt ]
&=&R_{1}J+ E\mathrm {e}^{-\frac {1}{\left( R_{1}+R_{2}\right)C}t}-R_{1}J\mathrm {e}^{-\frac {1}{\left( R_{1}+R_{2}\right)C}t} \\[ 5pt ]
&=& E\mathrm {e}^{-\frac {1}{\left( R_{1}+R_{2}\right)C}t}+R_{1}J\left\{ 1-\mathrm {e}^{-\frac {1}{\left( R_{1}+R_{2}\right)C}t}\right\} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。したがって,(2)は\( \ \displaystyle -\frac {1}{C\left( R_{1}+R_{2}\right) } \ \)となる。
(3)解答:ル
(2)解答式より,(3)は\( \ R_{1}J \ \)と求められる。
(4)解答:ヨ
(5)解答:チ
(2)より,定常状態\( \ v_{s}=R_{1}J \ \)で一定であるため,③式より,
\[
\begin{eqnarray}
i_{2s}&=&C\frac {\mathrm {d}v_{s}}{\mathrm {d}t} \\[ 5pt ]
&=&0 \\[ 5pt ]
\end{eqnarray}
\]
となり,これと①式より,
\[
\begin{eqnarray}
J &=&i_{1s}+i_{2s} \\[ 5pt ]
i_{1s}&=&J-i_{2s} \\[ 5pt ]
&=&J \\[ 5pt ]
\end{eqnarray}
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは