《理論》〈電子理論〉[H19:問8]トランジスタの電流帰還バイアス回路に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

次の文章は，トランジスタ回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる数値を解答群の中から選び，その記号をマークシートに記入しなさい。

図1のトランジスタ回路において，\( \ v_{in} \ \)は正弦波入力信号電圧，\( \ v_{o1} \ \)，\( \ v_{o2} \ \)は正弦波出力信号電圧である。いま，ベース直流電流\( \ I_{B} \ \)が抵抗\( \ R_{A} \ \)を流れる直流電流\( \ I_{A} \ \)に比較して十分小さいと仮定すると，ベースの直流電圧は\( \ V_{B}= \ \fbox {　 （１） 　} \ \mathrm {[V]} \ \)となる。さらに，トランジスタのベース－エミッタ間の直流電圧を\( \ V_{BE}= 0.7 \ \mathrm {[V]} \ \)と仮定すると，エミッタ直流電流は\( \ I_{E}= \ \fbox {　 （２） 　} \ \mathrm {[mA]} \ \)と求められる。

ここで，トランジスタの交流等価回路が図2で表され，また，すべてのコンデンサを正弦波交流信号の周波数において短絡と見なすと，\( \ v_{o1} \ \)を出力電圧としたときの電圧増幅度は，\( \ \displaystyle \frac {v_{o1}}{v_{in}}≒ \ \fbox {　 （３） 　} \ \)倍である。さらに，出力電圧を\( \ v_{o2} \ \)とするときの電圧増幅度は，\( \ \displaystyle \frac {v_{o2}}{v_{in}}≒ \ \fbox {　 （４） 　} \ \)倍である。したがって，\( \ v_{o1} \ \)と\( \ v_{o2} \ \)の位相差は\( \ \fbox {　 （５） 　} \ \)である。

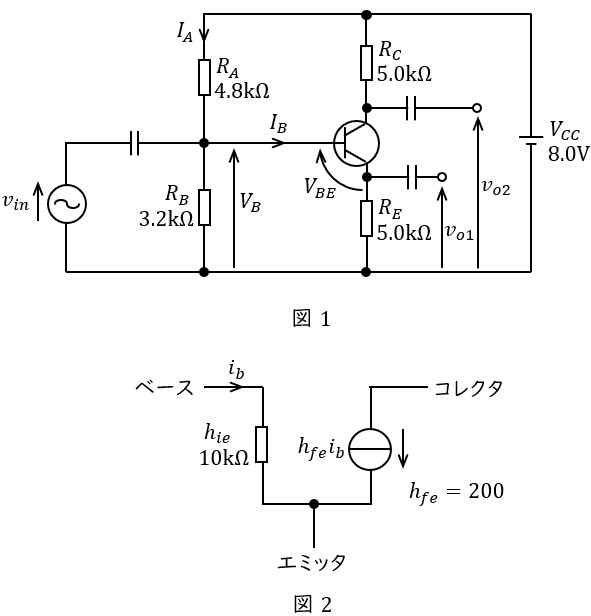
〔問8の解答群〕
\[
\begin{eqnarray}
&（イ）&　1.0　　　　　　　&（ロ）&　8.0　　　　　　　&（ハ）&　0.8 \\[ 5pt ] &（ニ）&　100　　　　　&（ホ）&　0^{\circ }　　　　　&（ヘ）&　3.2 \\[ 5pt ] &（ト）&　2.0　　　　　&（チ）&　0.5　　　　　&（リ）&　-100 \\[ 5pt ] &（ヌ）&　4.8 　　　　　&（ル）&　180^{\circ }　　　　　&（ヲ）&　0.1 \\[ 5pt ] &（ワ）&　90^{\circ }　　　　　&（カ）&　1.5　　　　　&（ヨ）&　-1.0 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

電流帰還バイアス回路の回路演算に関する問題です。
本問のような電流帰還バイアス回路の問題は図2のように等価回路が与えられるため，基本的な電気回路の公式以外特別な知識は必要ありません。したがって，解法を理解することが重要です。
解法手順もほぼ決まっていますので，本問でしっかりと理解して類題が出題されても解けるようにしておきましょう。

【解答】

(1)解答：ヘ
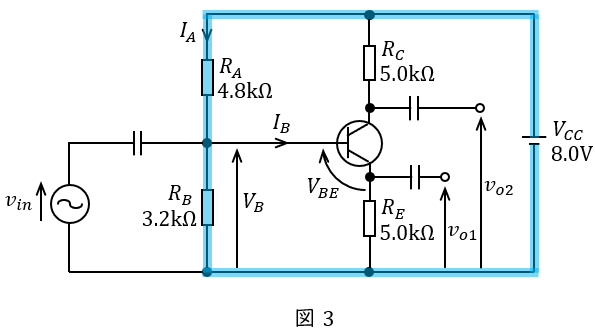
ベース直流\( \ I_{B} \ \)が十分に小さいとしたとき，図3に示す閉回路に分圧の法則を適用すると，
\[
\begin{eqnarray}
V_{B} &=&\frac {R_{B}}{R_{A}+R_{B}}V_{CC} \\[ 5pt ] &=&\frac {3.2}{4.8+3.2}\times 8.0 \\[ 5pt ] &=&3.2 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：チ
\( \ V_{BE}= 0.7 \ \mathrm {[V]} \ \)とすると，エミッタの直流電圧\( \ V_{E} \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
V_{E} &=&V_{B}-V_{BE} \\[ 5pt ] &=&3.2-0.7 \\[ 5pt ] &=&2.5 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となるから，エミッタ直流電流\( \ I_{E} \ \mathrm {[mA]} \ \)は，
\[
\begin{eqnarray}
I_{E} &=&\frac {V_{E}}{R_{E}} \\[ 5pt ] &=&\frac {2.5}{5.0\times 10^{3}} \\[ 5pt ] &=&0.5\times 10^{-3} \ \mathrm {[A]}　→　0.5 \ \mathrm {[mA]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：イ
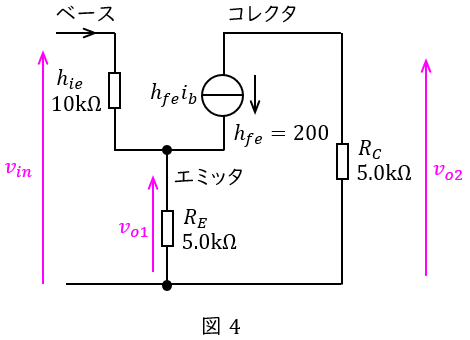
正弦波交流信号のみを考えたとき，コンデンサ及び直流電圧源は短絡と考えればよいので，等価回路は図4のようになる。
図4より，エミッタに流れる電流\( \ i_{e} \ \)は，
\[
\begin{eqnarray}
i_{e} &=&i_{b}+h_{fe}i_{b} \\[ 5pt ] &=&i_{b}+200i_{b} \\[ 5pt ] &=&201i_{b} \\[ 5pt ] \end{eqnarray}
\] となり，これより\( \ \displaystyle \frac {v_{o1}}{v_{in}} \ \)は，
\[
\begin{eqnarray}
\frac {v_{o1}}{v_{in}} &=&\frac {R_{E}i_{e}}{h_{ie}i_{b}+R_{E}i_{e}} \\[ 5pt ] &=&\frac {5.0\times 10^{3}\times 201i_{b}}{10.0\times 10^{3}i_{b}+5.0\times 10^{3}\times 201i_{b}} \\[ 5pt ] &=&\frac {5.0\times 201}{10.0+5.0\times 201} \\[ 5pt ] &≒&0.99　→　1.0 \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ヨ
(3)と同様に図4より\( \ \displaystyle \frac {v_{o2}}{v_{in}} \ \)は，
\[
\begin{eqnarray}
\frac {v_{o2}}{v_{in}} &=&\frac {-R_{C}h_{fe}i_{b}}{h_{ie}i_{b}+R_{E}i_{e}} \\[ 5pt ] &=&-\frac {5.0\times 10^{3}\times 200i_{b}}{10.0\times 10^{3}i_{b}+5.0\times 10^{3}\times 201i_{b}} \\[ 5pt ] &=&-\frac {5.0\times 200}{10.0+5.0\times 201} \\[ 5pt ] &≒&-0.99　→　-1.0 \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ル
(3)及び(4)解答式より，\( \ v_{o1} \ \)と\( \ v_{o2} \ \)は大きさがほぼ同じで向きが逆なので，位相差は\( \ 180^{\circ } \ \)と求められる。