《電力・管理》〈変電〉[R07:問3]百分率インピーダンスを用いた電圧降下と短絡容量計算に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

図のような一次側が\( \ 154 \ \mathrm {kV} \ \)，二次側が\( \ 77 \ \mathrm {kV} \ \)の変圧器\( \ 3 \ \)台で連系された\( \ \mathrm {B} \ \)変電所がある。この変電所が\( \ 40 \ \mathrm {km} \ \)の\( \ 1 \ \)回線送電線で\( \ \mathrm {A} \ \)変電所から受電しているとき，次の問に答えよ。なお，各変圧器のインピーダンスと各変電所から電源側を見たインピーダンスはリアクタンスのみとし，その値は自己容量基準で図に示すとおりである。また，\( \ \mathrm {B} \ \)変電所の一次側の電圧は\( \ 154 \ \mathrm {kV} \ \)一定で，送電線のリアクタンス\( \ X_{\mathrm {L}} \ \)は\( \ 100 \ \mathrm {MV\cdot A} \ \)，\( \ 154 \ \mathrm {kV} \ \)基準で\( \ 0.16 \ \mathrm {％ / km} \ \)とし，抵抗，アドミタンスは無視するものとする。

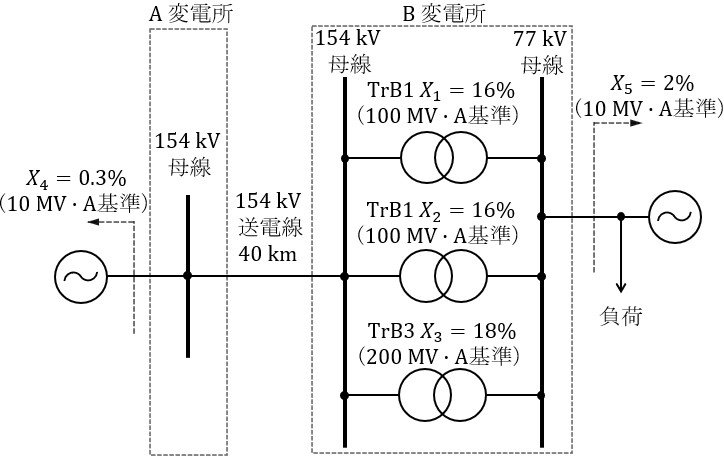
(1)　\( \ \mathrm {B} \ \)変電所の一次側母線が\( \ 100 \ \mathrm {MW}+\mathrm {j}20 \ \mathrm {Mvar} \ \)（遅れ無効電力を正）で受電しているとき，送電端の\( \ \mathrm {A} \ \)変電所の送り出し電圧\( \ \mathrm {[kV]} \ \)を求めよ。ただし，電圧計算の近似式は用いないこと。

(2)　\( \ 77 \ \mathrm {kV} \ \)母線の短絡容量\( \ P_{\mathrm {s}} \ \mathrm {[MV\cdot A]} \ \)を求めよ。なお，単位法における基準容量は\( \ 100 \ \mathrm {MV\cdot A} \ \)として計算せよ。

【ワンポイント解説】

百分率インピーダンスを用いた電圧降下と短絡容量計算に関する問題です。
考え方は難解ではありませんが，計算量が多いため，慎重かつ正確性が求められる問題です。難解な令和7年電力・管理科目において合否を分ける重要な問題と言えるかもしれません。
平成29年問3でも類題が出題されていますので，本問を学習した後チャレンジしてみて下さい。

1.オーム法から百分率インピーダンス法への変換
基準容量を\( \ P_{\mathrm {n}} \ \mathrm {[V\cdot A]} \ \)，基準電圧を\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \)，基準電流を\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)とすると，\( \ Z \ \mathrm {[\Omega ]} \ \)の百分率インピーダンス（パーセントインピーダンス）\( \ ％Z \ \mathrm {[％]} \ \)は，
\[
\begin{eqnarray}
％Z&=&\frac {ZI_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}\times 100 (定義) \\[ 5pt ] &=&\frac {\sqrt {3}ZI_{\mathrm {n}}}{V_{\mathrm {n}}}\times 100 \\[ 5pt ] &=&\frac {\sqrt {3}ZV_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}}\times 100 \\[ 5pt ] &=&\frac {P_{\mathrm {n}}Z}{V_{\mathrm {n}}^{2}}\times 100　　 (∵P_{\mathrm {n}}=\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} ) \\[ 5pt ] \end{eqnarray}
\] となります。

2.百分率インピーダンスの容量換算
「1.オーム法からパーセントインピーダンス法への変換」の通り，百分率インピーダンスは基準容量に比例します。したがって，基準容量\( \ P_{\mathrm {A}} \ \mathrm {[V\cdot A]} \ \)から\( \ P_{\mathrm {B}} \ \mathrm {[V\cdot A]} \ \)へ変換する場合の百分率インピーダンスは，
\[
\begin{eqnarray}
％Z_{\mathrm {B}}&=&\frac {P_{\mathrm {B}}}{P_{\mathrm {A}}}％Z_{\mathrm {A}} \\[ 5pt ] \end{eqnarray}
\] となります。

3.百分率インピーダンスによる短絡電流と短絡容量の計算
百分率インピーダンスを\( \ ％Z \ \mathrm {[％]} \ \)とすると，三相短絡電流\( \ I_{\mathrm {s}} \ \mathrm {[A]} \ \)は，基準電流\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)を用いて，
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {I_{\mathrm {n}}}{％Z／100} \\[ 5pt ] &=&\frac {100I_{\mathrm {n}}}{％Z} \\[ 5pt ] \end{eqnarray}
\] で求められます。また，短絡容量\( \ P_{\mathrm {s}} \ \mathrm {[V\cdot A]} \ \)は，基準容量\( \ P_{\mathrm {n}} \ \mathrm {[A]} \ \)を用いて，
\[
\begin{eqnarray}
P_{\mathrm {s}}&=&\frac {100P_{\mathrm {n}}}{％Z} \\[ 5pt ] \end{eqnarray}
\] で求められます。

※百分率インピーダンスの定義式等を用いて\( \ \displaystyle I_{\mathrm {s}}=\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}} \ \)から上式を求めることはできますが，試験時には暗記しておいた方が良いと思います。
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}{Z_{\mathrm {s}} \ \mathrm {[\Omega ]}} \\[ 5pt ] &=&\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}} \\[ 5pt ] &=&\frac {V_{\mathrm {n}}I_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}I_{\mathrm {n}}} \\[ 5pt ] &=&\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}I_{\mathrm {n}}}\times I_{\mathrm {n}} \\[ 5pt ] &=&\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}I_{\mathrm {n}}\times 100}\times 100I_{\mathrm {n}} \\[ 5pt ] &=&\frac {100I_{\mathrm {n}}}{％Z_{\mathrm {s}}} \\[ 5pt ] \end{eqnarray}
\]

4.複素電力
三相線路において，送電端電圧（相電圧）を\( \ {\dot E}_{\mathrm {s}} \ \mathrm {[V]} \ \)，受電端電圧（相電圧）を\( \ {\dot E}_{\mathrm {r}} \ \mathrm {[V]} \ \)，線路電流を\( \ \dot I \ \mathrm {[A]} \ \)とすると，受電端への送電電力\( \ P+\mathrm {j}Q \ \mathrm {[V\cdot A]} \ \)は遅れ無効電力を正とすると，
\[
\begin{eqnarray}
P+\mathrm {j}Q&=&3{\dot E}_{\mathrm {r}}\overline {\dot I} \\[ 5pt ] \end{eqnarray}
\] で求められます。ただし，\( \ \overline {\dot I} \ \)は\( \ \dot I \ \)の共役複素数であり，\( \ \dot I =I_{\mathrm {r}}+\mathrm {j}I_{\mathrm {i}} \ \)であるとき，\( \ \overline {\dot I}=I_{\mathrm {r}}-\mathrm {j}I_{\mathrm {i}} \ \)となります。

【解答】

(1)送電端の\( \ \mathrm {A} \ \)変電所の送り出し電圧\( \ \mathrm {[kV]} \ \)
\( \ 154 \ \mathrm {kV} \ \)送電線の百分率インピーダンス\( \ ％X_{\mathrm {l}} \ \mathrm {[％]} \ \)は，
\[
\begin{eqnarray}
％X_{\mathrm {l}} &=&0.16\times 40 \\[ 5pt ] &=&6.4 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] であるため，送電線のリアクタンス\( \ X_{\mathrm {l}} \ \mathrm {[\Omega ]} \ \)は，基準容量\( \ P_{\mathrm {n}}=100 \ \mathrm {[MV\cdot A]} \ \)，基準電圧\( \ V_{\mathrm {n}}=154 \ \mathrm {[kV]} \ \)であるから，ワンポイント解説「1.オーム法から百分率インピーダンス法への変換」の通り，
\[
\begin{eqnarray}
％X_{\mathrm {l}} &=&\frac {P_{\mathrm {n}}X_{\mathrm {l}}}{V_{\mathrm {n}}^{2}}\times 100 \\[ 5pt ] X_{\mathrm {l}}&=&\frac {％X_{\mathrm {l}}V_{\mathrm {n}}^{2}}{100P_{\mathrm {n}}} \\[ 5pt ] &=&\frac {6.4\times \left( 154\times 10^{3}\right) ^{2}}{100\times 100\times 10^{6}} \\[ 5pt ] &≒&15.178 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となる。送電線を流れる電流\( \ \dot I _{\mathrm {l}} \ \mathrm {[A]} \ \)は，受電電力\( \ P+\mathrm {j}Q=100+\mathrm {j}20 \ \mathrm {[MV\cdot A]} \ \)，\( \ \mathrm {B} \ \)変電所の一次側の電圧\( \ V_{\mathrm {r}}=154 \ \mathrm {[kV]} \ \)であるから，ワンポイント解説「4.複素電力」の通り，
\[
\begin{eqnarray}
P+\mathrm {j}Q&=&\sqrt {3}{\dot V}_{\mathrm {r}}\overline {\dot I_{\mathrm {l}}} \\[ 5pt ] \overline {\dot I_{\mathrm {l}}}&=&\frac {P+\mathrm {j}Q}{\sqrt {3}{\dot V}_{\mathrm {r}}} \\[ 5pt ] \dot I_{\mathrm {l}}&=&\frac {P-\mathrm {j}Q}{\sqrt {3}\overline {{\dot V}_{\mathrm {r}}}} \\[ 5pt ] &=&\frac {100\times 10^{6}-\mathrm {j}20\times 10^{6}}{\sqrt {3}\times 154\times 10^{3}} \\[ 5pt ] &≒&374.90-\mathrm {j}74.981 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，送電端電圧\( \ \dot V_{\mathrm {s}} \ \mathrm {[kV]} \ \)は，
\[
\begin{eqnarray}
\frac {\dot V_{\mathrm {s}}}{\sqrt {3}}&=&\frac {\dot V_{\mathrm {r}}}{\sqrt {3}}+\mathrm {j}X_{\mathrm {l}}\dot I_{\mathrm {l}} \\[ 5pt ] \dot V_{\mathrm {s}}&=&\dot V_{\mathrm {r}}+\mathrm {j}\sqrt {3}X_{\mathrm {l}}\dot I_{\mathrm {l}} \\[ 5pt ] &=&154\times 10^{3}+\mathrm {j}\sqrt {3}\times 15.178\times \left( 374.90-\mathrm {j}74.981\right) \\[ 5pt ] &≒&154\times 10^{3}+1 \ 971.2+\mathrm {j}9 \ 855.8 \\[ 5pt ] &≒&155 \ 970+\mathrm {j}9 \ 855.8 \ \mathrm {[V]}　→　155.97+\mathrm {j}9.855 \ 8 \ \mathrm {[kV]} \\[ 5pt ] \end{eqnarray}
\] となり，その大きさ\( \ V_{\mathrm {s}} \ \mathrm {[kV]} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {s}}&=&\sqrt {155.97^{2}+9.855 \ 8^{2}} \\[ 5pt ] &≒&156.28　→　156 \ \mathrm {[kV]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)\( \ 77 \ \mathrm {kV} \ \)母線の短絡容量\( \ P_{\mathrm {s}} \ \mathrm {[MV\cdot A]} \ \)
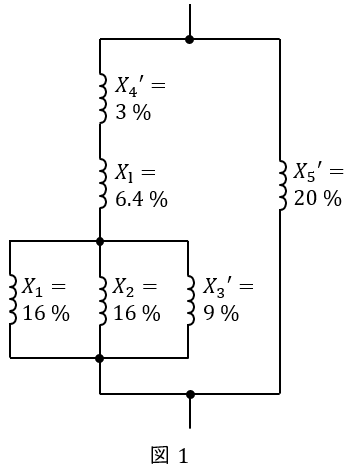
\( \ X_{3}=18 \ \mathrm {[％]} \ \)，\( \ X_{4}=0.3 \ \mathrm {[％]} \ \)，\( \ X_{5}=2 \ \mathrm {[％]} \ \)を\( \ 100 \ \mathrm {MV\cdot A} \ \)換算すると，ワンポイント解説「2.百分率インピーダンスの容量換算」の通り，
\[
\begin{eqnarray}
{X_{3}}^{\prime }&=&\frac {100}{200}\times 18 \\[ 5pt ] &=&9 \ \mathrm {[％]} \\[ 5pt ] {X_{4}}^{\prime }&=&\frac {100}{10}\times 0.3 \\[ 5pt ] &=&3 \ \mathrm {[％]} \\[ 5pt ] {X_{5}}^{\prime }&=&\frac {100}{10}\times 2 \\[ 5pt ] &=&20 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] となり，\( \ 77 \ \mathrm {kV} \ \)母線からみたインピーダンスは図1の通りとなる。図1より，\( \ X_{1} \ \)，\( \ X_{2} \ \)，\( \ {X_{3}}^{\prime } \ \)の合成リアクタンス\( \ X_{123} \ \mathrm {[％]} \ \)は，
\[
\begin{eqnarray}
\frac {1}{X_{123}}&=&\frac {1}{X_{1}}+\frac {1}{X_{2}}+\frac {1}{{X_{3}}^{\prime }} \\[ 5pt ] &=&\frac {1}{16}+\frac {1}{16}+\frac {1}{9} \\[ 5pt ] &=&\frac {9+9+16}{144} \\[ 5pt ] &=&\frac {17}{72} \\[ 5pt ] X_{123}&≒&4.235 \ 3 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] となり，全体の合成リアクタンス\( \ X \ \mathrm {[％]} \ \)は，
\[
\begin{eqnarray}
X&=&\frac {\left( {X_{4}}^{\prime }+X_{\mathrm {l}}+X_{123}\right) {X_{5}}^{\prime }}{\left( {X_{4}}^{\prime }+X_{\mathrm {l}}+X_{123}\right) +{X_{5}}^{\prime }} \\[ 5pt ] &=&\frac {\left( 3+6.4+4.235 \ 3\right) \times 20}{\left( 3+6.4+4.235 \ 3\right) + 20} \\[ 5pt ] &=&8.107 \ 7 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，短絡容量\( \ P_{\mathrm {s}} \ \mathrm {[MV\cdot A]} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {s}}&=&\frac {100P_{\mathrm {n}}}{X} \\[ 5pt ] &=&\frac {100\times 100}{8.107 \ 7} \\[ 5pt ] &≒&1 \ 230 \ \mathrm {[MV\cdot A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。