《電力・管理》〈配電〉[H29:問4]配電線間の潮流に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】
- 3.1 【本問に関する質疑応答】

【問題】

【難易度】★★★☆☆（普通）

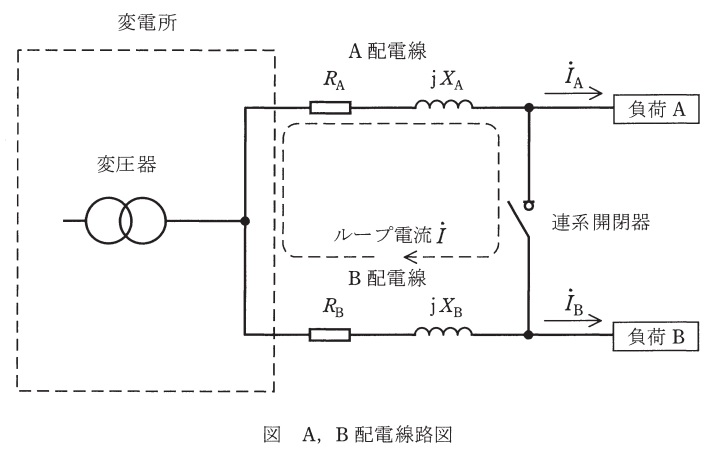
図に示すように変電所の同一のバンクから\( \ \mathrm {A} \ \)配電線と\( \ \mathrm {B} \ \)配電線の\( \ 2 \ \)回線が引き出されており，負荷はそれぞれの配電系統の末端に集中して接続されているものとする。配電線路運用における区間切り換えのため，以下に示す条件のもとで連系開閉器を投入したときの連系点の電圧が\( \ 6.6 \ \mathrm {kV} \ \)になった際の，図に示す連系点に流れるループ電流\( \ \dot I \ \)の大きさを以下の小問に従って答えよ。ただし，それぞれの配電系統のインピーダンス及び系統末端負荷への供給電力は以下に示される条件とし，連系線のインピーダンスは\( \ 0 \ \Omega \ \)で，かつ，連系開閉器投入後も各負荷の消費電力は変化がないもの(定電力負荷)とする。

［条件］
・\( \ \mathrm {A} \ \)配電線の末端負荷への供給電力
　　有効電力\( \ 2400 \ \mathrm {kW} \ \)，進み無効電力\( \ 800 \ \mathrm {kvar} \ \)
・\( \ \mathrm {A} \ \)配電線のインピーダンス
　　　\(\displaystyle \dot Z_{\mathrm {A}}=R_{\mathrm {A}}+\mathrm {j}X_{\mathrm {A}}=0.3+\mathrm {j}0.39 \ \Omega \)
・B配電線の末端負荷への供給電力
　　有効電力\( \ 1715 \ \mathrm {kW} \ \)，遅れ無効電力\( \ 457 \ \mathrm {kvar} \ \)
・B配電線のインピーダンス
　　　\(\displaystyle \dot Z_{\mathrm {B}}=R_{\mathrm {B}}+\mathrm {j}X_{\mathrm {B}}=0.2+\mathrm {j}0.16 \ \Omega \)

(1)　連系開閉器投入後の負荷電流\( \ {\dot I}_{\mathrm {A}} \ \)，\( \ {\dot I}_{\mathrm {B}} \ \)を，連系点の電圧の位相を基準(位相\( \ 0 \ \))として求めよ。

(2)　(1)を用いて連系点に流れるループ電流\( \ \dot I \ \)の大きさを求めよ。

【ワンポイント解説】

問題内容自体はさほど難しい問題ではありませんが，(2)の計算が非常に面倒な問題です。二次試験の場合，例え計算間違いしたとしても，計算過程を丁寧に書くことで部分点を期待できると思います。

【解答】

(1)連系開閉器投入後の負荷電流\( \ {\dot I}_{\mathrm {A}} \ \)，\( \ {\dot I}_{\mathrm {B}} \ \)
負荷\( \ \mathrm {A} \ \)の電力を\( \ P_{\mathrm {A}}-\mathrm {j}Q_{\mathrm {A}}=2400-\mathrm {j}800 \ \)，電流を\( \ \dot I_{\mathrm {A}} \ \)，負荷\( \ \mathrm {B} \ \)の電力を\( \ P_{\mathrm {B}}+\mathrm {j}Q_{\mathrm {B}}=1715+\mathrm {j}457 \ \)，電流を\( \ \dot I_{\mathrm {B}} \ \)とし，連系線の電圧を\( \ V=6.6 \ \mathrm {kV} \ \)とする。
遅れ無効電力を正とすると，皮相電力\( \ P+\mathrm {j}Q \ \)と電圧\( \ \dot V \ \)，電流\( \ \dot I \ \)の間には\( \ P+\mathrm {j}Q=\sqrt {3}\dot V\overline {\dot {I}} \ \)の関係があるから，
\[
\begin{eqnarray}
\dot I_{\mathrm {A}} &=& \frac {\overline {P_{\mathrm {A}}-\mathrm {j}Q_{\mathrm {A}}}}{\sqrt {3}\overline {\dot {V}}} \\[ 5pt ] &=& \frac {2400+\mathrm {j}800}{\sqrt {3}\times 6.6} \\[ 5pt ] &≒& 209.95+\mathrm {j}69.982 \ [\mathrm {A}]　→　210+\mathrm {j}70.0 \ [\mathrm {A}] \\[ 5pt ] \dot I_{\mathrm {B}} &=& \frac {\overline {P_{\mathrm {B}}+\mathrm {j}Q_{\mathrm {B}}}}{\sqrt {3}\overline {\dot {V}}} \\[ 5pt ] &=& \frac {1715-\mathrm {j}457}{\sqrt {3}\times 6.6} \\[ 5pt ] &≒& 150.02-\mathrm {j}39.977 \ [\mathrm {A}]　→　150-\mathrm {j}40.0 \ [\mathrm {A}] \end{eqnarray}
\] と求められる。

(2)連系点に流れるループ電流\( \ \dot I \ \)の大きさ
\( \ \displaystyle \dot Z_{\mathrm {A}}=R_{\mathrm {A}}+\mathrm {j}X_{\mathrm {A}} \ \)に流れる電流を\( \ \dot I_{\mathrm {a}} \ \)，\( \ \displaystyle \dot Z_{\mathrm {B}}=R_{\mathrm {B}}+\mathrm {j}X_{\mathrm {B}} \ \)に流れる電流を\( \ \dot I_{\mathrm {b}} \ \)とすると，連系線の抵抗が\( \ 0 \ \Omega \ \)であるから，
\[
\begin{eqnarray}
&\dot I_{\mathrm {a}}&=\dot I_{\mathrm {A}}+\dot I　　&・・・・・・・　①& \\[ 5pt ] &\dot I_{\mathrm {b}}&=\dot I_{\mathrm {B}}-\dot I　　&・・・・・・・　②& \\[ 5pt ] &\dot Z_{\mathrm {A}}&\dot I_{\mathrm {a}}=\dot Z_{\mathrm {B}}\dot I_{\mathrm {b}}　&・・・・・・・　③&
\end{eqnarray}
\] の関係が成り立つ。①，②を③に代入して\( \ \dot I \ \)について整理すると，
\[
\begin{eqnarray}
\dot Z_{\mathrm {A}}(\dot I_{\mathrm {A}}+\dot I) &=& \dot Z_{\mathrm {B}}(\dot I_{\mathrm {B}}-\dot I) \\[ 5pt ] (\dot Z_{\mathrm {A}}+\dot Z_{\mathrm {B}})\dot I &=& -\dot Z_{\mathrm {A}}\dot I_{\mathrm {A}}+\dot Z_{\mathrm {B}}\dot I_{\mathrm {B}} \\[ 5pt ] \dot I &=& \frac {-\dot Z_{\mathrm {A}}\dot I_{\mathrm {A}}+\dot Z_{\mathrm {B}}\dot I_{\mathrm {B}}}{\dot Z_{\mathrm {A}}+\dot Z_{\mathrm {B}}} \\[ 5pt ] \end{eqnarray}
\] となる。各値を代入すると，
\[
\begin{eqnarray}
\dot I &=& \frac {-(0.3+\mathrm {j}0.39)(209.95+\mathrm {j}69.982)+(0.2+\mathrm {j}0.16)(150.02-\mathrm {j}39.977)}{(0.3+\mathrm {j}0.39)+(0.2+\mathrm {j}0.16)} \\[ 5pt ] &=& \frac {0.70830-\mathrm {j}86.867}{0.5+\mathrm {j}0.55} \\[ 5pt ] &=& \frac {-47.423-\mathrm {j}43.824}{0.5525} \\[ 5pt ] &≒& -85.833-\mathrm {j}79.319 \ [\mathrm {A}] \\[ 5pt ] \end{eqnarray}
\] となる。よって，\( \ \dot I \ \)の大きさは，
\[
\begin{eqnarray}
\left| \dot I\right| &=& \sqrt{(-85.833)^{2}+(-79.319)^{2}} \\[ 5pt ] &≒& 116.87　→　117 \ \left[ \mathrm {A}\right] \\[ 5pt ] \end{eqnarray}
\] と求められる。