《電力・管理》〈電気施設管理〉[H26:問5]太陽電池発電所を設置した際の電圧上昇に関する計算・論説問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】
- 3.1 【本問に関する質疑応答】

【問題】

【難易度】★★★☆☆（普通）

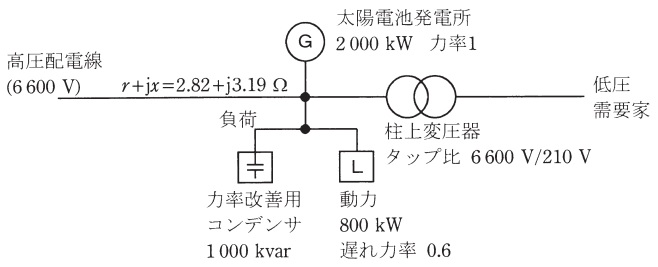
図に示すような三相3線式高圧配電線の末端に負荷が接続されており，新たに太陽電池発電所を設置した場合の逆潮流による電圧上昇について，次の問に答えよ。

ただし，低圧需要家側の電流は無視し，計算諸元は次のとおりとする。

・高圧配電線電圧：高圧\(6600 \ \mathrm {V}\)

・高圧配電線インピーダンス：\(r+\mathrm {j}x=2.82+\mathrm {j}3.19 \ \Omega \)

・柱上変圧器のタップ比：一次電圧／二次電圧　\(6600 \ \mathrm {V}／210 \ \mathrm {V}\)

・負荷：動力\(800 \ \mathrm {kW}\)，遅れ力率\(0.6\)
　　　　力率改善用コンデンサ\(1000 \ \mathrm {kvar}\)

・太陽電池発電所：出力\(2000 \ \mathrm {kW}\)，力率\(1\)

・電流値計算にあたっては，高圧配電線電圧\(6600 \ \mathrm {V}\)を用いる

(1)　負荷側に流れる有効電流\(I_{\mathrm {PL}} \ \mathrm {[ A ] }\)と無効電流\(I_{\mathrm {QL}} \ \mathrm {[ A ] }\)を求めよ。

(2)　太陽電池発電所が接続されることによる低圧需要家側の受電電圧\(V_{\mathrm {L}} \ \mathrm {[ V ] }\)を求めよ。ただし，逆潮流による配電線の電圧上昇\(\Delta V\)は，負荷側に流れる電流を正とした場合，
\[
\begin{eqnarray}
\Delta V &=&-\sqrt {3}(有効電流\times 線路の抵抗分+無効電流\times 線路のリアクタンス分) \\[ 5pt ] \end{eqnarray}
\] 　　で求めよ。

(3)　上記(2)で求めた受電電圧\(V_{\mathrm {L}} \ \mathrm {[ V ] }\)は，法令で定める維持すべき電圧をいくら超えているか。その値\(V_{\mathrm {D}} \ \mathrm {[ V ] }\)を求めよ。

(4)　高圧配電線，負荷，太陽電池発電所及び柱上変圧器で考えられる電圧上昇抑制対策を二つ述べよ。

【ワンポイント解説】

太陽電池発電所を建設したことにより潮流計算から電圧上昇がどうなるかを求める，極めて近代的な問題と言えます。有効電流と無効電流の向きに注意して，電圧がどのように上昇するか考え解くようにして下さい。

1.電気事業法施行規則における維持すべき電圧
電気事業法施行規則第44条において維持すべき電圧は以下のように定められています。
\[
\begin{array}{|c|c|}
\hline
標準電圧 & 維持すべき値 \\
\hline
100 \ \mathrm {[ V ] } & 101±6 \ \mathrm {[ V ] } \\
\hline
200 \ \mathrm {[ V ] } & 202±20 \ \mathrm {[ V ] } \\
\hline
\end{array}
\]

【解答】

(1)負荷側に流れる有効電流\(I_{\mathrm {PL}} \ \mathrm {[ A ] }\)と無効電流\(I_{\mathrm {QL}} \ \mathrm {[ A ] }\)
負荷の有効電力\(P\)と無効電力\(Q\)の大きさは，
\[
\begin{eqnarray}
P &=&800 \ \mathrm {[ kW ] } \\[ 5pt ] Q &=&800\times \frac {\sqrt {1-0.6^{2}}}{0.6} -1000 \\[ 5pt ] &≒&66.667 \ \mathrm {[kvar]} \\[ 5pt ] \end{eqnarray}
\] であるから，負荷側に流れる有効電流\(I_{\mathrm {PL}} \ \mathrm {[ A ] }\)と無効電流\(I_{\mathrm {QL}} \ \mathrm {[ A ] }\)の大きさは，
\[
\begin{eqnarray}
I_{\mathrm {PL}} &=&\frac {P}{\sqrt {3}\times 6600} \\[ 5pt ] &=&\frac {800\times 10^{3}}{\sqrt {3}\times 6600} \\[ 5pt ] &≒&69.981　→　70.0 \ \mathrm {[A]} \\[ 5pt ] I_{\mathrm {QL}} &=&\frac {Q}{\sqrt {3}\times 6600} \\[ 5pt ] &=&\frac {66.667\times 10^{3}}{\sqrt {3}\times 6600} \\[ 5pt ] &≒&5.8319　→　5.83 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)太陽電池発電所が接続されることによる低圧需要家側の受電電圧\(V_{\mathrm {L}} \ \mathrm {[ V ] }\)
太陽電池発電所を接続することによる逆潮流\(I_{\mathrm {G}} \ \mathrm {[ A ] }\)は力率が1であるから，すべて有効電流となり，その大きさは，
\[
\begin{eqnarray}
I_{\mathrm {G}} &=& \frac {2000\times 10^{3}}{\sqrt {3}\times 6600} \\[ 5pt ] &≒&174.95 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，設問にて与えられた電圧上昇の式より，配電線の電圧上昇\(\Delta V\)は，負荷側に流れる電流を正とすると，
\[
\begin{eqnarray}
\Delta V &=&-\sqrt {3}\left[ \left( I_{\mathrm {PL}}-I_{\mathrm {G}}\right) r+I_{\mathrm {QL}} x\right] \\[ 5pt ] &=&-\sqrt {3}\left[ \left( 69.981-174.95\right) \times 2.82+ 5.8319 \times 3.19\right] \\[ 5pt ] &≒&480.50 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。よって，低圧需要家側の受電電圧\(V_{\mathrm {L}}\)はタップ比が与えられているので，
\[
\begin{eqnarray}
V_{\mathrm {L}} &=&\frac {210}{6600}\left( 6600 +\Delta V\right) \\[ 5pt ] &=&\frac {210}{6600}\left( 6600 +480.50\right) \\[ 5pt ] &≒&225.29　→　225 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)受電電圧の法令超過値\(V_{\mathrm {D}} \ \mathrm {[ V ] }\)
ワンポイント解説「1.電気事業法施行規則における維持すべき電圧」より，\(200 \ \mathrm {[ V ] }\)配電線での最大電圧は\(222 \ \mathrm {[ V ] }\)であるから，法令超過値\(V_{\mathrm {D}} \ \mathrm {[ V ] }\)は，
\[
\begin{eqnarray}
V_{\mathrm {D}} &=&225.29-222 \\[ 5pt ] &=&3.29 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)高圧配電線，負荷，太陽電池発電所及び柱上変圧器で考えられる電圧上昇抑制対策を二つ
(ポイント)
・電圧上昇対策の基本（夜間・軽負荷時の対策）を思い出し，記載すれば特に問題ないと思います。
・実際には設備を設置する際にSVC(無効電力補償装置)を設置することが多いと聞いたことがあります。

(試験センター解答例)
・電線を太くしインピーダンスを減少
・力率改善用コンデンサの開放
・新たな無効電力補償装置の設置
・太陽電池発電設備側でインバータによる無効電力補償の増
・柱上変圧器のタップ変更