《電力・管理》〈送電〉[H29:問3]送電線の電圧変動率に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

図のような一次側が\( \ 154 \ \mathrm {kV} \ \)，二次側が\( \ 77 \ \mathrm {kV} \ \)の変圧器3台で連系された変電所がある。この変電所の\( \ 77 \ \mathrm {kV} \ \)側母線に接続された\( \ 30 \ \mathrm {MV\cdot A} \ \)の電力用コンデンサを投入したとき，次の問に答えよ。なお，各変圧器のインピーダンスはリアクタンスのみとし，その値は自己容量基準で図に示すとおりである。

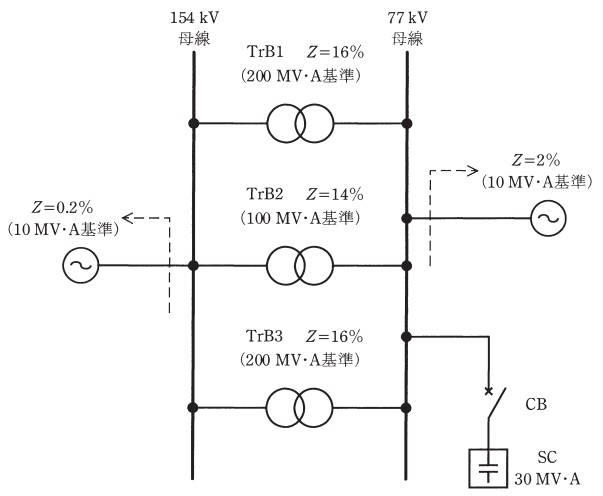
(1)　\( \ 77 \ \mathrm {kV} \ \)母線の短絡容量\( \ P_{\mathrm {S}} \ \mathrm {[MV\cdot A]} \ \)を求めよ。なお，単位法における基準容量は\( \ 100 \ \mathrm {MV\cdot A} \ \)として計算せよ。

(2)　電力用コンデンサを投入したときの\( \ 77 \ \mathrm {kV} \ \)側母線の基準電圧に対する電圧変動率\( \ \Delta V_{77} \ [％] \ \)を求めよ。

(3)　電力用コンデンサを投入したときの\( \ 154 \ \mathrm {kV} \ \)側母線の基準電圧に対する電圧変動率\( \ \Delta V_{154} \ [％] \ \)を求めよ。

【ワンポイント解説】

単位法では基準容量を揃え，インピーダンスマップの等価回路を作成することが重要です。単位法は頻出問題なので，下記の単位法の定義式はよく理解しておきましょう。

1.百分率インピーダンスの定義
基準容量\( \ P_{\mathrm {n}} \ \)，基準電圧\( \ V_{\mathrm {n}} \ \)，基準電流\( \ I_{\mathrm {n}} \ \)とすると，インピーダンス\( \ Z \ \mathrm {[\Omega ]} \ \)の百分率インピーダンス\( \ ％Z \ \mathrm {[％]} \ \)は
\[
\begin{eqnarray}
％Z&=&\frac {ZI_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}\times 100=\frac {\sqrt {3}ZI_{\mathrm {n}}}{V_{\mathrm {n}}}\times 100 \\[ 5pt ] \end{eqnarray}
\] で定義されます。\( \ P_{\mathrm {n}}=\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} \ \)の関係を用いて，定義式を整理すると，
\[
\begin{eqnarray}
％Z&=&\frac {\sqrt {3}ZV_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}}\times 100 \\[ 5pt ] &=&\frac {ZP_{\mathrm {n}}}{V_{\mathrm {n}}^{2}}\times 100 \\[ 5pt ] \end{eqnarray}
\] となります。

2.短絡容量\( \ P_{\mathrm {S}} \ \)
三相短絡事故が発生した際の短絡容量\( \ P_{\mathrm {S}} \ \)は，その時の公称電圧\( \ V_{\mathrm {B}} \ \)，その時流れる三相短絡電流を\( \ I_{\mathrm {S}} \ \)とすると，
\[
P_{\mathrm {S}}=\sqrt {3}V_{\mathrm {B}}I_{\mathrm {S}}
\] となります。

【解答】

(1)\( \ 77 \ \mathrm {kV} \ \)母線の短絡容量\( \ P_{\mathrm {S}} \ \mathrm {[MV\cdot A]} \ \)
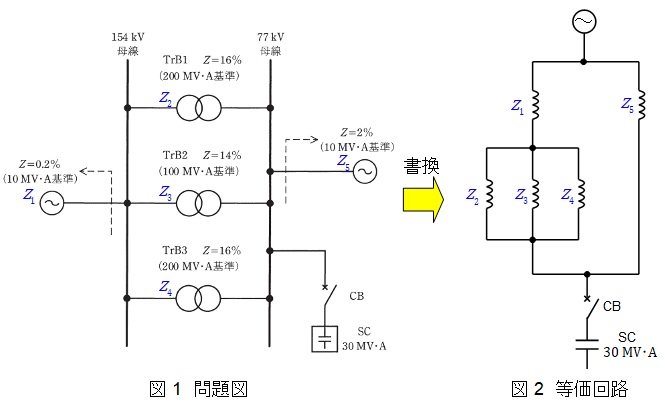
図1のように各インピーダンスを\( \ Z_{1}～Z_{5} \ \)とおくと，それぞれの\( \ 100 \ \mathrm {MV\cdot A} \ \)ベースの百分率インピーダンスは，
\[
\begin{eqnarray}
Z_{1}&=&\frac {100\mathrm {MV\cdot A}}{10\mathrm {MV\cdot A}}\times 0.2 \\[ 5pt ] &=&2 \ [％] \\[ 5pt ] Z_{2}&=&Z_{4}=\frac {100\mathrm {MV\cdot A}}{200\mathrm {MV\cdot A}}\times 16 \\[ 5pt ] &=&8 \ [％] \\[ 5pt ] Z_{5}&=&\frac {100\mathrm {MV\cdot A}}{10\mathrm {MV\cdot A}}\times 2 \\[ 5pt ] &=&20 \ [％] \\[ 5pt ] \end{eqnarray}
\] となり，図1の等価回路は図2のように書くことができる。\( \ Z_{2} \ \)，\( \ Z_{3} \ \)，\( \ Z_{4} \ \)の並列合成インピーダンス\( \ Z_{\mathrm {T}} \ \)は，
\[
\begin{eqnarray}
Z_{\mathrm {T}} &=& \frac {1}{\displaystyle \frac {1}{Z_{2}}+\frac {1}{Z_{3}}+\frac {1}{Z_{4}}} \\[ 5pt ] &=& \frac {1}{\displaystyle \frac {1}{8％}+\frac {1}{14％}+\frac {1}{8％}} \\[ 5pt ] &≒& 3.1111 \ [％] \\[ 5pt ] \end{eqnarray}
\] となる。よって，\( \ Z_{1} \ \)，\( \ Z_{\mathrm {T}} \ \)，\( \ Z_{5} \ \)を合成した短絡インピーダンス\( \ Z_{\mathrm {S}} \ \)は，
\[
\begin{eqnarray}
Z_{\mathrm {S}} &=& \frac {1}{\displaystyle \frac {1}{Z_{5}}+\frac {1}{Z_{1}+Z_{\mathrm {T}}}} \\[ 5pt ] &=& \frac {1}{\displaystyle \frac {1}{20％}+\frac {1}{2％+3.1111％}} \\[ 5pt ] &≒& 4.0708 \ [％] \\[ 5pt ] \end{eqnarray}
\] となる。したがって，\( \ 77 \ \mathrm {kV} \ \)母線の短絡容量\( \ P_{\mathrm {S}} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {S}} &=& \frac {100}{Z_{\mathrm {S}}}\times P_{\mathrm {B}} \\[ 5pt ] &=& \frac {100}{4.0708}\times 100 \\[ 5pt ] &≒& 2456.5　→　2460 \ [\mathrm {MV\cdot A}] \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)電力用コンデンサを投入したときの\( \ 77 \ \mathrm {kV} \ \)側母線の基準電圧に対する電圧変動率\( \ \Delta V_{77} \ [％] \ \)
基準電圧\( \ V_{\mathrm {B}} \ \)，電圧変化量を\( \ v \ \)とすると，電圧変動率\( \ \Delta V_{77} \ \)は，
\[
\begin{eqnarray}
\Delta V_{77} &=& \frac {v}{\displaystyle \frac {V_{\mathrm {B}}}{\sqrt {3}}}\times 100 \\[ 5pt ] &=& \frac {\sqrt {3}v}{V_{\mathrm {B}}}\times 100 \\[ 5pt ] \end{eqnarray}
\] となる。ここで，コンデンサ投入時に流れる電流を\( \ I_{\mathrm {C}} \ \)，\( \ 77 \ \mathrm {kV} \ \)母線から電源側を見たインピーダンスを\( \ Z \ \)とすると，
\[
\begin{eqnarray}
v&=&ZI_{\mathrm {C}} \\[ 5pt ] \end{eqnarray}
\] となるから，
\[
\begin{eqnarray}
\Delta V_{77} &=& \frac {\sqrt {3}ZI_{\mathrm {C}}}{V_{\mathrm {B}}}\times 100 \\[ 5pt ] &=& \frac {\sqrt {3}ZV_{\mathrm {B}}I_{\mathrm {C}}}{V_{\mathrm {B}}^{2}}\times 100 \\[ 5pt ] \end{eqnarray}
\] と変形できる。ここで，コンデンサの容量\( \ Q \ \)とすると,\( \ Q=\sqrt {3}V_{\mathrm {B}}I_{\mathrm {C}} \ \)となり，短絡容量\( \ P_{\mathrm {S}} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {S}} &=& \sqrt {3}V_{\mathrm {B}}I_{\mathrm {S}} \\[ 5pt ] &=& \sqrt {3}V_{\mathrm {B}}\frac {\displaystyle \frac {V_{\mathrm {B}}}{\sqrt {3}}}{Z} \\[ 5pt ] &=& \frac {V_{\mathrm {B}}^{2}}{Z}
\end{eqnarray}
\] となるから，
\[
\begin{eqnarray}
\Delta V_{77}&=&\frac {Q}{P_{\mathrm {S}}}\times 100 \\[ 5pt ] \end{eqnarray}
\] となり，各値を代入すると，
\[
\begin{eqnarray}
\Delta V_{77} &=& \frac {30}{2456.5}\times 100 \\[ 5pt ] &=& 1.2212　→　1.22 \ [％] \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)電力用コンデンサを投入したときの\( \ 154 \ \mathrm {kV} \ \)側母線の基準電圧に対する電圧変動率\( \ \Delta V_{154} \ [％] \ \)
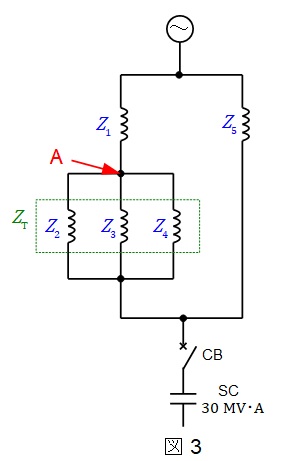
\( \ 154 \ \mathrm {kV} \ \)母線の電圧変動率\( \ \Delta V_{154} \ [％] \ \)は図3のＡでの電圧変動率となる。したがって，電圧変動率は\( \ Z_{1} \ \)と\( \ Z_{\mathrm {T}} \ \)より，
\[
\begin{eqnarray}
\Delta V_{154} &=& \frac {Z_{1}}{Z_{1}+Z_{\mathrm {T}}}\Delta V_{77} \\[ 5pt ] &=& \frac {2}{2+3.1111}\times 1.2212 \\[ 5pt ] &≒& 0.47786　→　0.478 \ [％] \\[ 5pt ] \end{eqnarray}
\] と求められる。