《機械》〈パワーエレクトロニクス〉[R02:問2]降圧チョッパの電圧及び損失に関する計算・空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
- 2.1 【関連する「電気の神髄」記事】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，降圧チョッパに関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

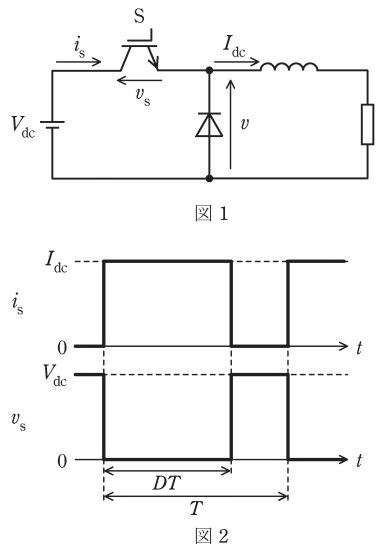
図1は降圧チョッパの回路図である。この回路は直流電圧源$ \ V_{\mathrm {dc}} \ $を入力とし，出力電流$ \ I_{\mathrm {dc}} \ $が半導体スイッチ$ \ \mathrm {S} \ $とダイオードの間を転流する代表的な電力変換回路である。インダクタンスは十分に大きく，電流$ \ I_{\mathrm {dc}} \ $にリプル成分は無いものとする。また，ダイオードの順電圧降下は無視する。

図1の半導体スイッチ$ \ \mathrm {S} \ $を理想的であると仮定した場合の電流$ \ i_{\mathrm {s}} \ $と電圧$ \ v_{\mathrm {s}} \ $の波形を図2に示す。スイッチ$ \ \mathrm {S} \ $は定数$ \ D \ \left( 0≦D≦1 \right) \ $とスイッチング周期$ \ T \ $の積である$ \ DT \ $の期間に導通し，$ \ D \ $を$ \ \fbox {　（１）　} \ $と呼ぶ。ダイオード電圧$ \ v \ $の平均値$ \ V \ $は$ \ V= \ \fbox {　（２）　} \ $と表され，$ \ D \ $を変化させることによってダイオード電圧$ \ v \ $の平均値を変えることができる。図2のどの時刻でも，理想的な半導体スイッチ$ \ \mathrm {S} \ $の電流$ \ i_{\mathrm {s}} \ $と電圧$ \ v_{\mathrm {s}} \ $の一方は零であることから，スイッチング損失は発生しない。

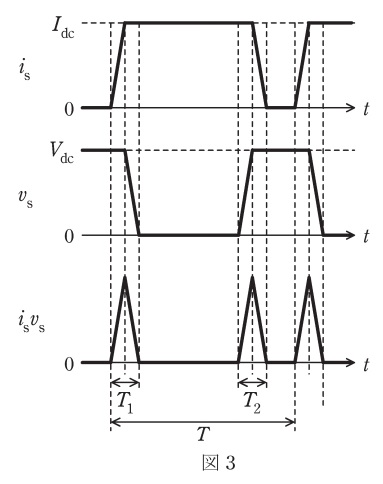
半導体スイッチ$ \ \mathrm {S} \ $のターンオン期間とターンオフ期間を考慮するため，図3に示す電流$ \ i_{\mathrm {s}} \ $と電圧$ \ v_{\mathrm {s}} \ $のモデル波形を考えてみよう。ターンオフ期間とターンオン期間には，電流$ \ i_{\mathrm {s}} \ $と電圧$ \ v_{\mathrm {s}} \ $が共に$ \ \fbox {　（３）　} \ $期間が存在する。図3において，ターンオフ期間では$ \ v_{\mathrm {s}}=V_{\mathrm {dc}} \ $となった後に電流$ \ i_{\mathrm {s}} \ $は減少し，ターンオン期間では$ \ i_{\mathrm {s}}=I_{\mathrm {dc}} \ $となった後に電圧$ \ v_{\mathrm {s}} \ $は低下する。そのため，半導体スイッチ$ \ \mathrm {S} \ $は損失を発生し，そのエネルギーは電流$ \ i_{\mathrm {s}} \ $と電圧$ \ v_{\mathrm {s}} \ $の積$ \ i_{\mathrm {s}}v_{\mathrm {s}} \ $の面積によって求められる。電流$ \ i_{\mathrm {s}} \ $と電圧$ \ v_{\mathrm {s}} \ $の変化は直線的と仮定すると，$ \ 1 \ $回のターンオフ期間の損失$ \ W_{\mathrm {off}} \ \mathrm {[J]} \ $は$ \ W_{\mathrm {off}}= \ \fbox {　（４）　} \ $である。$ \ 1 \ $回のターンオン期間の損失$ \ W_{\mathrm {on}} \ \mathrm {[J]} \ $も同様に求められる。したがって，半導体スイッチ$ \ \mathrm {S} \ $におけるスイッチング損失$ \ P_{\mathrm {s}} \ \mathrm {[W]} \ $は$ \ P_{\mathrm {s}}= \ \fbox {　（５）　} \ $である。

〔問2の解答群〕
\[
\begin{eqnarray}
&（イ）&　負である　　　　　&（ロ）&　\left( \frac {1}{1-D}\right) V_{\mathrm {dc}}　　　　　&（ハ）&　零である \\[ 5pt ] &（ニ）&　\frac {W_{\mathrm {off}}-W_{\mathrm {on}}}{T}　　　　　&（ホ）&　\frac {W_{\mathrm {off}}+W_{\mathrm {on}}}{T}　　　　　&（ヘ）&　\frac {1}{6}V_{\mathrm {dc}}I_{\mathrm {dc}}T_{2} \\[ 5pt ] &（ト）&　DV_{\mathrm {dc}}　　　　　&（チ）&　\frac {1}{2}V_{\mathrm {dc}}I_{\mathrm {dc}}T_{1}　　　　　　&（リ）&　\frac {1}{2}V_{\mathrm {dc}}I_{\mathrm {dc}}T_{2} \\[ 5pt ] &（ヌ）&　\frac {1}{6}V_{\mathrm {dc}}I_{\mathrm {dc}}T_{1}　　　　　&（ル）&　W_{\mathrm {off}}+W_{\mathrm {on}}　　　　　&（ヲ）&　還流率 \\[ 5pt ] &（ワ）&　\left( \frac {D}{1-D}\right) V_{\mathrm {dc}}　　　　　&（カ）&　通流率　　　　　&（ヨ）&　正である \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

降圧チョッパに関する問題です。
降圧チョッパのメカニズムは直流チョッパの中でも最も理解しやすく基本となるので，確実に理解するようにしましょう。
後半は$ \ 2 \ $種らしい受験生に試験中で考えさせるような問題となっています。

1.降圧チョッパの動作
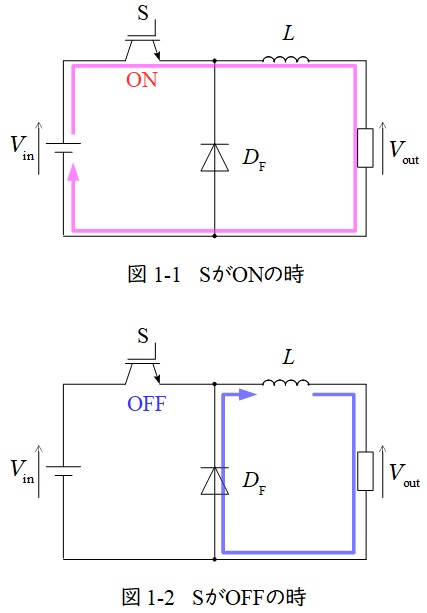
図1-1及び図1-2は降圧チョッパの例となります。
スイッチ$ \ \mathrm {S} \ $がオンになると，図1-1のように電源からの電流はスイッチ$ \ \mathrm {S} \ $を通り，リアクトル$ \ L \ $側に電流が流れますが，ダイオード$ \ D_{\mathrm {F}} \ $は逆向きなので電流が流れません。
スイッチ$ \ \mathrm {S} \ $がオフになると，図1-2のように電源から電流は流れず，リアクトルに蓄えられてるエネルギーから出力側と還流ダイオード$ \ D_{\mathrm {F}} \ $に電流が流れます。
したがって降圧チョッパの出力電圧の平均値$ \ V_{\mathrm {out}} \ $は，スイッチのオン時間を$ \ T_{\mathrm {on}} \ $，オフ時間を$ \ T_{\mathrm {off}} \ $とすると，
\[
\begin{eqnarray}
V_{\mathrm {out}}&=&\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}V_{\mathrm {in}} \\[ 5pt ] \end{eqnarray}
\] で求められます。このとき，$ \ V_{\mathrm {in}} \ $の係数
\[
\begin{eqnarray}
\gamma &=&\frac {T_{\mathrm {ON}}}{T_{\mathrm {ON}}+T_{\mathrm {OFF}}} \\[ 5pt ] \end{eqnarray}
\] を通流率といいます。

【関連する「電気の神髄」記事】

　　降圧チョッパ回路の理論

【解答】

(1)解答：カ
題意より解答候補は，（ヲ）還流率，（カ）通流率，になると思います。
ワンポイント解説「1.降圧チョッパの動作」の通り，通流率$ \ D \ $とすると，
\[
\begin{eqnarray}
D &=&\frac {T_{\mathrm {ON}}}{T} \\[ 5pt ] T_{\mathrm {ON}} &=&DT \\[ 5pt ] \end{eqnarray}
\] となるので，通流率が適切となります。

(2)解答：ト
ダイオード電圧$ \ v \ $はスイッチがオンの時導通しないため$ \ V_{\mathrm {dc}} \ $がかかり，スイッチがオフの時導通するので$ \ 0 \ \mathrm {V} \ $となる。
したがって，その平均値$ \ V \ $は，
\[
\begin{eqnarray}
V &=&\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}V_{\mathrm {dc}} \\[ 5pt ] &=&DV_{\mathrm {dc}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ヨ
題意より解答候補は，（イ）負である，（ハ）零である，（ヨ）正である，になると思います。
図3より，スイッチが切換わる期間には$ \ i_{\mathrm {s}} \ $及び$ \ v_{\mathrm {s}} \ $共に正である部分が存在していることがわかります。

(4)解答：リ
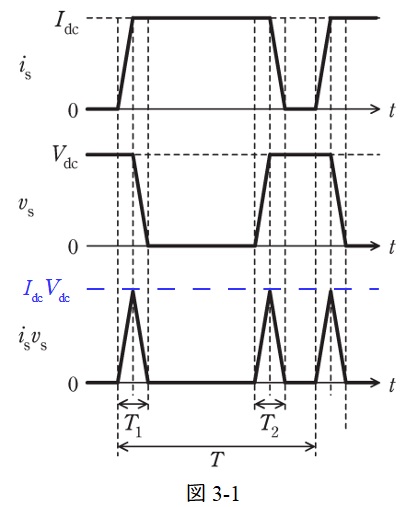
図3-1の通り，スイッチ切換え時の損失の最大値は$ \ I_{\mathrm {dc}}V_{\mathrm {dc}} \ $である。
また，ターンオフ時間はスイッチング素子の電流$ \ i_{\mathrm {s}} \ $が$ \ I_{\mathrm {dc}} \ $から$ \ 0 \ $になるタイミングなので$ \ T_{2} \ $となる。
したがって$ \ 1 \ $回のターンオフ期間の損失$ \ W_{\mathrm {off}} \ \mathrm {[J]} \ $を三角形の面積により求めると，
\[
\begin{eqnarray}
W_{\mathrm {off}} &=&\frac {T_{2}\cdot I_{\mathrm {dc}}V_{\mathrm {dc}}}{2} \\[ 5pt ] &=&\frac {1}{2}V_{\mathrm {dc}}I_{\mathrm {dc}}T_{2}\\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ホ
スイッチング周期$ \ T \ $の間にターンオフ期間の損失$ \ W_{\mathrm {off}} \ \mathrm {[J]} \ $とターンオン期間の損失$ \ W_{\mathrm {on}} \ \mathrm {[J]} \ $が$ \ 1 \ $回ずつあるので，単位時間当たりのスイッチング損失$ \ P_{\mathrm {s}} \ \mathrm {[W]} \ $は，
\[
\begin{eqnarray}
P_{\mathrm {s}} &=&\frac {W_{\mathrm {off}}+W_{\mathrm {on}}}{T} \\[ 5pt ] \end{eqnarray}
\] と求められる。