Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
次の文章は,変圧器の結線と送電電力の関係に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選びなさい。
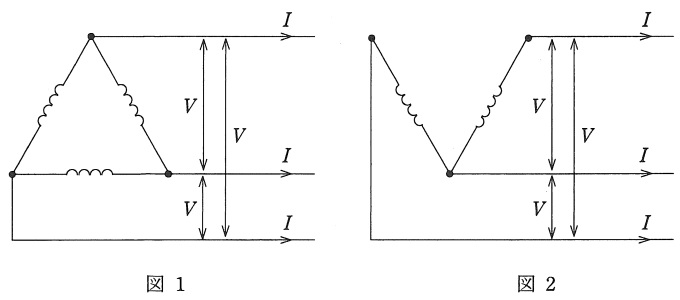
図1のように単相変圧器\( \ 3 \ \)台を\( \ \mathrm {\Delta } \ \)結線した場合と,図2のように単相変圧器\( \ 2 \ \)台を\( \ \mathrm {V} \ \)結線した場合とを考える。この変圧器が電圧\( \ V \ \mathrm {[V]} \ \),電流\( \ I \ \mathrm {[A]} \ \),力率\( \ \cos \theta \ \)の三相平衡負荷に送電している場合を考える。図1の場合,それぞれの変圧器を流れる電流は\( \ \fbox { (1) } \ \mathrm {[A]} \ \),変圧器\( \ 1 \ \)台当たり必要となる容量は\( \ \fbox { (2) } \ \mathrm {[V\cdot A]} \ \)であり,変圧器\( \ 3 \ \)台の送電電力の合計は\( \ \fbox { (3) } \ \mathrm {[W]} \ \)となる。また,図2の場合,変圧器\( \ 1 \ \)台当たり必要となる容量は\( \ \fbox { (4) } \ \mathrm {[V\cdot A]} \ \)であり,変圧器\( \ 2 \ \)台の送電電力の合計は\( \ \fbox { (3) } \ \mathrm {[W]} \ \)となる。したがって,同じ電力を送電する場合に必要となる変圧器\( \ 1 \ \)台当たりの容量は,\( \ \mathrm {\Delta } \ \)結線が\( \ \mathrm {V} \ \)結線の約\( \ \fbox { (5) } \ \mathrm {[%]} \ \)となる。
〔問2の解答群〕
\[
\begin{eqnarray}
&(イ)& \sqrt {3}VI\cos \theta &(ロ)& \sqrt {3}I &(ハ)& \frac {VI\cos \theta }{\sqrt {3}} \\[ 5pt ]
&(ニ)& \frac {VI}{\sqrt {3}} &(ホ)& \frac {2VI}{\sqrt {3}} &(ヘ)& 50 \\[ 5pt ]
&(ト)& VI &(チ)& I &(リ)& 58 \\[ 5pt ]
&(ヌ)& 67 &(ル)& 2VI\cos \theta &(ヲ)& \frac {I}{\sqrt {3}} \\[ 5pt ]
&(ワ)& 3VI\cos \theta &(カ)& VI\cos \theta &(ヨ)& \sqrt {3}VI \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
変圧器の\( \ \mathrm {\Delta } \ \)結線と\( \ \mathrm {V} \ \)結線の比較に関する問題です。
\( \ 3 \ \)種の時は利用率や出力比を丸暗記で対応していた方も多いと思いますが,\( \ 2 \ \)種の場合は二次試験のことも考えると下記のようなメカニズムはある程度理解していた方が良いと思います。
1.\( \ \mathrm {\Delta -\Delta } \ \)結線と\( \ \mathrm {V-V} \ \)結線の比較
①\( \ \mathrm {\Delta -\Delta } \ \)結線
\( \ \mathrm {\Delta -\Delta } \ \)結線の変圧器の回路図とベクトル図を図3及び図4に示します。
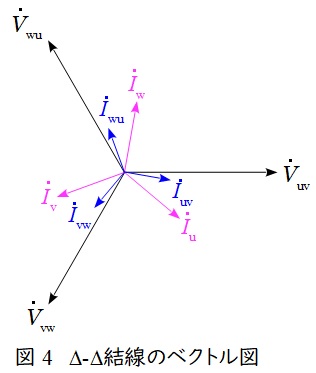
図3において,負荷電流\( \ {\dot I}_{\mathrm {u}} \ \mathrm {[A]} \ \)は,変圧器を流れる電流\( \ {\dot I}_{\mathrm {uv}} \ \mathrm {[A]} \ \)及び\( \ {\dot I}_{\mathrm {wu}} \ \mathrm {[A]} \ \)を用いて,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {u}}&=& {\dot I}_{\mathrm {uv}}-{\dot I}_{\mathrm {wu}} \\[ 5pt ]
\end{eqnarray}
\]
で求められ,ベクトル図上では図4のような関係となり,三相平衡である場合にはそれぞれの大きさの比は,
\[
\begin{eqnarray}
I_{\mathrm {u}}&=& \sqrt {3}I_{\mathrm {uv}} \\[ 5pt ]
\end{eqnarray}
\]
であることが分かります。したがって,各変圧器が分担する容量\( \ S \ \mathrm {[V\cdot A]} \ \)は,負荷の線間電圧を\( \ V_{\mathrm {uv}}=V_{\mathrm {vw}}=V_{\mathrm {wu}}=V \ \),負荷電流を\( \ I_{\mathrm {u}}=I_{\mathrm {v}}=I_{\mathrm {w}}=I \ \)とすると,
\[
\begin{eqnarray}
S&=& \frac {VI}{\sqrt {3}} \\[ 5pt ]
\end{eqnarray}
\]
となります。したがって,変圧器全体の送電電力\( \ P \ \mathrm {[W]} \ \)は力率を\( \ \cos \theta \ \)とすると,
\[
\begin{eqnarray}
P&=& 3S\cos \theta \\[ 5pt ]
&=& 3\cdot \frac {VI}{\sqrt {3}}\cdot \cos \theta \\[ 5pt ]
&=&\sqrt {3}VI \cos \theta \\[ 5pt ]
\end{eqnarray}
\]
となります。

②\( \ \mathrm {V -V } \ \)結線
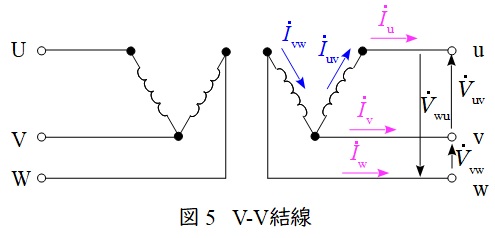
\( \ \mathrm {V -V } \ \)結線の変圧器の回路図とベクトル図を図5及び図6に示します。
図5において,負荷電流\( \ {\dot I}_{\mathrm {u}} \ \mathrm {[A]} \ \),\( \ {\dot I}_{\mathrm {v}} \ \mathrm {[A]} \ \),\( \ {\dot I}_{\mathrm {w}} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {u}}&=& {\dot I}_{\mathrm {uv}} \\[ 5pt ]
{\dot I}_{\mathrm {v}}&=& {\dot I}_{\mathrm {vw}}-{\dot I}_{\mathrm {uv}} \\[ 5pt ]
{\dot I}_{\mathrm {w}}&=& -{\dot I}_{\mathrm {vw}} \\[ 5pt ]
\end{eqnarray}
\]
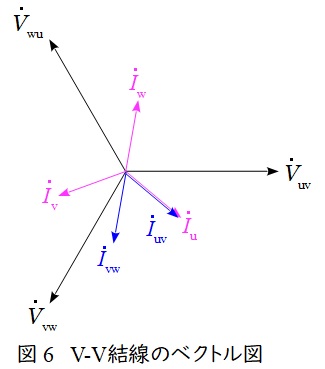
で求められ,ベクトル図上では図6のような関係となり,三相平衡である場合にはそれぞれの大きさの比は,
\[
\begin{eqnarray}
I_{\mathrm {u}}&=&I_{\mathrm {u}}&=&I_{\mathrm {u}}&=&I_{\mathrm {uv}}&=&I_{\mathrm {vw}} \\[ 5pt ]
\end{eqnarray}
\]
であることが分かります。したがって,各変圧器が分担する容量\( \ S \ \mathrm {[V\cdot A]} \ \)は,負荷の線間電圧を\( \ V_{\mathrm {uv}}=V_{\mathrm {vw}}=V_{\mathrm {wu}}=V \ \),負荷電流を\( \ I_{\mathrm {u}}=I_{\mathrm {v}}=I_{\mathrm {w}}=I \ \)とすると,
\[
\begin{eqnarray}
S&=& VI \\[ 5pt ]
\end{eqnarray}
\]
となります。変圧器全体の送電電力\( \ P_{\mathrm {V}} \ \mathrm {[W]} \ \)は力率を\( \ \cos \theta \ \)とすると,
\[
\begin{eqnarray}
P_{\mathrm {V}}&=& \sqrt {3}VI \cos \theta \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ \mathrm {V -V } \ \)結線で得られる出力\( \ \mathrm {[V\cdot A]} \ \)は各変圧器の出力の\( \ \sqrt {3} \ \)倍となるため,利用率は,
\[
\begin{eqnarray}
利用率&=& \frac {\sqrt {3}VI}{2VI} \\[ 5pt ]
&=& \frac {\sqrt {3}}{2} → 86.6 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
となります。また,\( \ \mathrm {V -V } \ \)結線と\( \ \mathrm {\Delta -\Delta } \ \)結線で同じ電力を出力する場合に必要となる変圧器の容量比は,
\[
\begin{eqnarray}
容量比&=& \frac {\displaystyle \frac {VI}{\sqrt {3}}}{VI} \\[ 5pt ]
&=& \frac {1}{\sqrt {3}} → 57.7 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
となるため,\( \ \mathrm {V -V } \ \)結線の出力は\( \ \mathrm {\Delta -\Delta } \ \)結線の\( \ 57.7 \ \mathrm {[%]} \ \)程度であることがわかります。
【解答】
(1)解答:ヲ
ワンポイント解説「1.\( \ \mathrm {\Delta -\Delta } \ \)結線と\( \ \mathrm {V-V} \ \)結線の比較」図4の通り,変圧器を流れる電流\( \ I_{\mathrm {p}} \ \)は,負荷電流\( \ I \ \)を用いると,
\[
\begin{eqnarray}
I_{\mathrm {p}}&=& \frac {I}{\sqrt {3}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ニ
図1の変圧器\( \ 1 \ \)台当たり必要となる容量\( \ S_{\mathrm {1}} \ \)は,ワンポイント解説「1.\( \ \mathrm {\Delta -\Delta } \ \)結線と\( \ \mathrm {V-V} \ \)結線の比較」の通り,
\[
\begin{eqnarray}
S_{\mathrm {1}}&=& VI_{\mathrm {p}} \\[ 5pt ]
&=&\frac {VI}{\sqrt {3}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:イ
変圧器\( \ 3 \ \)台の送電電力の合計\( \ P \ \)は,ワンポイント解説「1.\( \ \mathrm {\Delta -\Delta } \ \)結線と\( \ \mathrm {V-V} \ \)結線の比較」の通り,
\[
\begin{eqnarray}
P&=& 3S_{\mathrm {1}}\cos \theta \\[ 5pt ]
&=&3\cdot \frac {VI}{\sqrt {3}}\cos \theta \\[ 5pt ]
&=&\sqrt {3}VI\cos \theta \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ト
図2の変圧器\( \ 1 \ \)台当たり必要となる容量\( \ S_{\mathrm {2}} \ \)は,負荷電流と変圧器を流れる電流の大きさが等しいので,ワンポイント解説「1.\( \ \mathrm {\Delta -\Delta } \ \)結線と\( \ \mathrm {V-V} \ \)結線の比較」の通り,
\[
\begin{eqnarray}
S_{\mathrm {2}}&=& VI \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:リ
同じ電力を送電する場合に必要となる変圧器の容量比\( \ \displaystyle \frac {S_{\mathrm {1}}}{S_{\mathrm {2}}} \ \)は,(2)及び(4)より,
\[
\begin{eqnarray}
\frac {S_{\mathrm {1}}}{S_{\mathrm {2}}}&=& \frac {\displaystyle \frac {VI}{\sqrt {3}}}{VI} \\[ 5pt ]
&=& \frac {1}{\sqrt {3}} \\[ 5pt ]
&≒& 0.577 → 58 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは