《電力・管理》〈変電〉[H21:問2]調相設備接続前後の電圧降下と線路損失に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

図に示す\( \ 6 \ 600 \ \mathrm {[V]} \ \)，\( \ 50 \ \mathrm {[Hz]} \ \)の三相\( \ 3 \ \)線式配電線路において，変電所の\( \ \mathrm {A} \ \)点の電圧を\( \ 6 \ 600 \ \mathrm {[V]} \ \)，\( \ \mathrm {B} \ \)点の需要家負荷を\( \ 100 \ \mathrm {[A]} \ \)（遅れ力率\( \ 0.8 \ \)），また，線路末端の\( \ \mathrm {C} \ \)点の需要家負荷を\( \ 100 \ \mathrm {[A]} \ \)（遅れ力率\( \ 0.8 \ \)）とする。\( \ \mathrm {AB} \ \)間の長さを\( \ 2 \ \mathrm {[km]} \ \)，\( \ \mathrm {BC} \ \)間の長さを\( \ 4 \ \mathrm {[km]} \ \)とし，線路のインピーダンスは\( \ 1 \ \mathrm {[km]} \ \)当たりの抵抗を\( \ 0.4 \ \mathrm {[\Omega ]} \ \)，リアクタンスを\( \ 0.3 \ \mathrm {[\Omega ]} \ \)とする。次の問に答えよ。

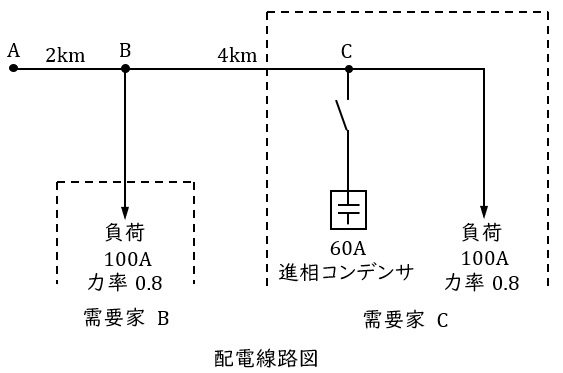
(1)　\( \ \mathrm {B} \ \)点，\( \ \mathrm {C} \ \)点の線間電圧をそれぞれ求めよ。

(2)　\( \ \mathrm {C} \ \)点に進相コンデンサを設置して，進相電流\( \ 60 \ \mathrm {[A]} \ \)を流して補償したとき，\( \ \mathrm {B} \ \)点及び\( \ \mathrm {C} \ \)点の線間電圧を求めよ。

(3)　進相コンデンサ設置前後の配電線路の損失を計算し，比較せよ。

【ワンポイント解説】

進相コンデンサ接続前後の電圧降下と線路損失を求める問題です。
考え方はそれほど難解ではありませんが，計算量が多いため，計算間違いに注意しなければならない問題です。
(2)は電流を求めてから解いても大丈夫ですが\( \ \mathrm {AB} \ \)間の力率が変わってしまうため，注意して解くようにして下さい。

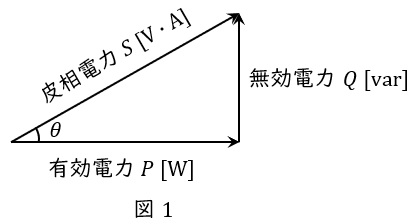
1.有効電力\( \ P \ \)と無効電力\( \ Q \ \)
抵抗で消費される電力を有効電力\( \ P \ \mathrm {[W]} \ \)，リアクタンスで消費もしくは供給される電力を無効電力\( \ Q \ \mathrm {[var]} \ \)と呼び，図1のようにベクトル図を描きます。さらに，有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)のベクトル和は皮相電力\( \ S \ \mathrm {[V\cdot A]} \ \)と呼ばれ，
\[
\begin{eqnarray}
S&=&\sqrt {P^{2}+Q^{2}} \\[ 5pt ] \end{eqnarray}
\] の関係があります。図1において，力率は\( \ \cos \theta \ \)で定義され，
\[
\begin{eqnarray}
\cos \theta &=&\frac {P}{S} \\[ 5pt ] \end{eqnarray}
\] となります。

2.送配電線の電圧降下
図3のような一般的な三相\( \ 3 \ \)線式送配電線路において，送配電線には抵抗\( \ R \ \mathrm {[\Omega ]} \ \)及びリアクタンス\( \ X \ \mathrm {[\Omega ]} \ \)があるため，送配電線での抵抗降下やリアクタンス降下が発生します。
送電端電圧（相電圧）を\( \ {\dot E}_{\mathrm {s}} \ \mathrm {[V]} \ \)，受電端に力率\( \ \cos \theta \ \)の負荷を接続したときの受電端電圧（相電圧）を\( \ {\dot E}_{\mathrm {r}} \ \mathrm {[V]} \ \)，送配電線に流れる電流を\( \ \dot I \ \mathrm {[A]} \ \)とすると，
\[
\begin{eqnarray}
{\dot E}_{\mathrm {s}} &=&{\dot E}_{\mathrm {r}}+\left( R+\mathrm {j}X \right) \dot I \\[ 5pt ] \end{eqnarray}
\] の関係があるため，ベクトル図で表すと図4のようになります。

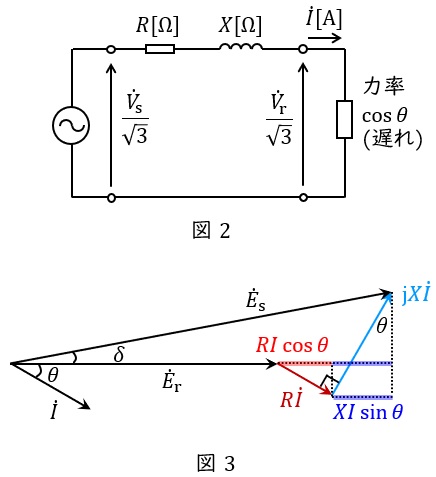
\( \ {\dot E}_{\mathrm {s}} \ \)と\( \ {\dot E}_{\mathrm {r}} \ \)の位相差が十分に小さいと仮定すると，線路の電圧降下\( \ \varepsilon =\sqrt {3}E_{\mathrm {s}}-\sqrt {3}E_{\mathrm {r}} \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
E_{\mathrm {s}}&≃&E_{\mathrm {r}}+RI\cos \theta +XI\sin \theta \\[ 5pt ] E_{\mathrm {s}}-E_{\mathrm {r}}&=&RI\cos \theta +XI\sin \theta \\[ 5pt ] \sqrt {3}E_{\mathrm {s}}-\sqrt {3}E_{\mathrm {r}}&=&\sqrt {3}\left( RI\cos \theta +XI\sin \theta \right) \\[ 5pt ] \varepsilon &=&\sqrt {3}I\left( R\cos \theta +X\sin \theta \right) \\[ 5pt ] \end{eqnarray}
\] で求められます。

3.三相\( \ 3 \ \)線式線路の電力損失
三相\( \ 3 \ \)線式送配電線路において，送配電線の\( \ 1 \ \)線あたりの抵抗\( \ R \ \mathrm {[\Omega ]} \ \)，流れる電流を\( \ I \ \mathrm {[A]} \ \)とすると，線路損失\( \ P_{\mathrm {L}} \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {L}} &=&3RI^{2} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)\( \ \mathrm {B} \ \)点，\( \ \mathrm {C} \ \)点の線間電圧
\( \ \mathrm {AB} \ \)間の抵抗\( \ R_{\mathrm {AB}} \ \mathrm {[\Omega ]} \ \)及びリアクタンス\( \ X_{\mathrm {AB}} \ \mathrm {[\Omega ]} \ \)，\( \ \mathrm {BC} \ \)間の抵抗\( \ R_{\mathrm {BC}} \ \mathrm {[\Omega ]} \ \)及びリアクタンス\( \ X_{\mathrm {BC}} \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
R_{\mathrm {AB}} &=&0.4\times 2 \\[ 5pt ] &=&0.8 \ \mathrm {[\Omega ]} \\[ 5pt ] X_{\mathrm {AB}} &=&0.3\times 2 \\[ 5pt ] &=&0.6 \ \mathrm {[\Omega ]} \\[ 5pt ] R_{\mathrm {BC}} &=&0.4\times 4 \\[ 5pt ] &=&1.6 \ \mathrm {[\Omega ]} \\[ 5pt ] X_{\mathrm {BC}} &=&0.3\times 4 \\[ 5pt ] &=&1.2 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
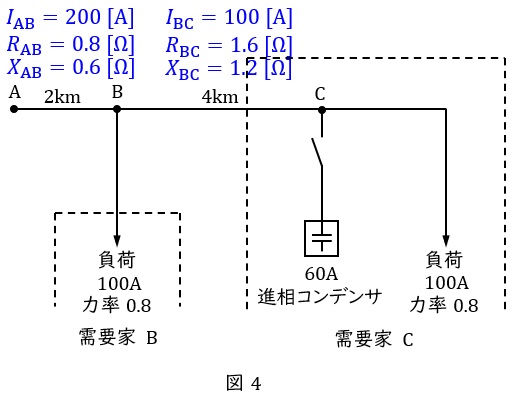
\] であり，コンデンサ接続前の\( \ \mathrm {AB} \ \)間の電流\( \ I_{\mathrm {AB}} \ \mathrm {[A]} \ \)及び\( \ \mathrm {BC} \ \)間の電流\( \ I_{\mathrm {BC}} \ \mathrm {[A]} \ \)は，力率がともに\( \ \cos \theta =0.8 \ \)であるから，
\[
\begin{eqnarray}
I_{\mathrm {AB}} &=&100+100 \\[ 5pt ] &=&200 \ \mathrm {[A]} \\[ 5pt ] I_{\mathrm {BC}} &=&100 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となるので，図4のようになる。

また，それぞれの負荷の\( \ \sin \theta \ \)は，
\[
\begin{eqnarray}
\sin \theta &=&\sqrt {1-\cos ^{2}\theta } \\[ 5pt ] &=&\sqrt {1-0.8^{2}} \\[ 5pt ] &=&0.6 \\[ 5pt ] \end{eqnarray}
\] となる。よって，\( \ \mathrm {B} \ \)点の線間電圧\( \ V_{\mathrm {B}} \ \mathrm {[V]} \ \)は，\( \ \mathrm {A} \ \)点の線間電圧\( \ V_{\mathrm {A}}=6 \ 600 \ \mathrm {[V]} \ \)であるから，ワンポイント解説「2.送配電線の電圧降下」の通り，
\[
\begin{eqnarray}
V_{\mathrm {A}}-V_{\mathrm {B}} &=&\sqrt {3}I_{\mathrm {AB}}\left( R_{\mathrm {AB}}\cos \theta +X_{\mathrm {AB}}\sin \theta \right) \\[ 5pt ] V_{\mathrm {B}} &=&V_{\mathrm {A}}-\sqrt {3}I_{\mathrm {AB}}\left( R_{\mathrm {AB}}\cos \theta +X_{\mathrm {AB}}\sin \theta \right) \\[ 5pt ] &=&6 \ 600-\sqrt {3}\times 200\times \left( 0.8\times 0.8 +0.6\times 0.6 \right) \\[ 5pt ] &≒&6 \ 600-346.41 \\[ 5pt ] &≒&6 \ 253.6　→　6 \ 250 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められ，同様に\( \ \mathrm {C} \ \)点の線間電圧\( \ V_{\mathrm {C}} \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {B}}-V_{\mathrm {C}} &=&\sqrt {3}I_{\mathrm {BC}}\left( R_{\mathrm {BC}}\cos \theta +X_{\mathrm {BC}}\sin \theta \right) \\[ 5pt ] V_{\mathrm {C}} &=&V_{\mathrm {B}}-\sqrt {3}I_{\mathrm {BC}}\left( R_{\mathrm {BC}}\cos \theta +X_{\mathrm {BC}}\sin \theta \right) \\[ 5pt ] &=&6 \ 253.6-\sqrt {3}\times 100\times \left( 1.6\times 0.8 +1.2\times 0.6 \right) \\[ 5pt ] &≒&6 \ 253.6-346.41 \\[ 5pt ] &≒&5 \ 907.2　→　5 \ 910 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)\( \ \mathrm {C} \ \)点に進相コンデンサを設置した後の\( \ \mathrm {B} \ \)点及び\( \ \mathrm {C} \ \)点の線間電圧
進相コンデンサに流れる電流\( \ I_{\mathrm {C}}=60 \ \mathrm {[A]} \ \)による\( \ \mathrm {AB} \ \)間の電圧降下\( \ v_{\mathrm {AB}} \ \mathrm {[V]} \ \)及び\( \ \mathrm {BC} \ \)間の電圧降下\( \ v_{\mathrm {BC}} \ \mathrm {[V]} \ \)は，力率が\( \ 0 \ \)（進み）であると考えれば良いので，
\[
\begin{eqnarray}
v_{\mathrm {AB}} &=&\sqrt {3}I_{\mathrm {C}}\left( R_{\mathrm {AB}}\times 0 -X_{\mathrm {AB}}\times 1 \right) \\[ 5pt ] &=&\sqrt {3}\times 60\times \left( 0 -0.6\times 1 \right) \\[ 5pt ] &≒&-62.354 \ \mathrm {[V]} \\[ 5pt ] v_{\mathrm {BC}} &=&\sqrt {3}I_{\mathrm {C}}\left( R_{\mathrm {BC}}\times 0 -X_{\mathrm {BC}}\times 1 \right) \\[ 5pt ] &=&\sqrt {3}\times 60\times \left( 0 -1.2\times 1 \right) \\[ 5pt ] &≒&-124.71 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，進相コンデンサを設置した後の\( \ \mathrm {B} \ \)点及び\( \ \mathrm {C} \ \)点の線間電圧\( \ V_{\mathrm {B}}^{\prime } \ \mathrm {[V]} \ \)及び\( \ V_{\mathrm {C}}^{\prime } \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {B}}^{\prime } &=&V_{\mathrm {B}}-v_{\mathrm {AB}} \\[ 5pt ] &=&6 \ 253.6-\left( -62.354\right) \\[ 5pt ] &≒&6316.0　→　6320 \ \mathrm {[V]} \\[ 5pt ] V_{\mathrm {C}}^{\prime } &=&V_{\mathrm {C}}-v_{\mathrm {AB}}-v_{\mathrm {BC}} \\[ 5pt ] &=&5 \ 907.2-\left( -62.354\right) -\left( -124.71\right) \\[ 5pt ] &≒&6 \ 094.3　→　6 \ 090 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)進相コンデンサ設置前後の配電線路の損失
コンデンサ接続前の線路損失\( \ W_{\mathrm {1}} \ \mathrm {[kW]} \ \)は，
\[
\begin{eqnarray}
W_{\mathrm {1}} &=&3R_{\mathrm {AB}}I_{\mathrm {AB}}^{2}+3R_{\mathrm {BC}}I_{\mathrm {BC}}^{2} \\[ 5pt ] &=&3\times 0.8\times 200^{2}+3\times 1.6\times 100^{2} \\[ 5pt ] &=&144 \ 000 \ \mathrm {[W]}　→　144 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] となる。\( \ \mathrm {C} \ \)点の需要家の負荷電流の有効成分\( \ I_{\mathrm {BCr}} \ \mathrm {[A]} \ \)と無効成分\( \ I_{\mathrm {BCi}} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {BCr}}&=&I_{\mathrm {BC}}\cos \theta \\[ 5pt ] &=&100\times 0.8 \\[ 5pt ] &=&80 \ \mathrm {[A]} \\[ 5pt ] I_{\mathrm {BCi}}&=&I_{\mathrm {BC}}\sin \theta \\[ 5pt ] &=&100\times 0.6 \\[ 5pt ] &=&60 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となり，コンデンサ電流\( \ I_{\mathrm {C}}=60 \ \mathrm {[A]} \ \)なので，無効成分はなくなりコンデンサ接続後の\( \ \mathrm {BC} \ \)間の電流\( \ I_{\mathrm {BC}}^{\prime } \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {BC}}^{\prime } &=&I_{\mathrm {BCr}} \\[ 5pt ] &=&80 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。また，\( \ \mathrm {AB} \ \)間の電流\( \ I_{\mathrm {AB}}^{\prime } \ \mathrm {[A]} \ \)は，\( \ \mathrm {B} \ \)点の需要家負荷が\( \ 100 \ \mathrm {[A]} \ \)なので，
\[
\begin{eqnarray}
I_{\mathrm {AB}}^{\prime } &=&\sqrt {\left( 100\cos \theta +I_{\mathrm {BC}}^{\prime }\right) ^{2}+\left( 100\sin \theta \right) ^{2}} \\[ 5pt ] &=&\sqrt {\left( 100\times 0.8 +80\right) ^{2}+\left( 100\times 0.6 \right) ^{2}} \\[ 5pt ] &=&\sqrt {29 \ 200} \\[ 5pt ] &≒&170.88 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。以上から，コンデンサ接続前の線路損失\( \ W_{\mathrm {2}} \ \mathrm {[kW]} \ \)は，
\[
\begin{eqnarray}
W_{\mathrm {2}} &=&3R_{\mathrm {AB}}{I_{\mathrm {AB}}^{\prime }}^{2}+3R_{\mathrm {BC}}{I_{\mathrm {BC}}^{\prime }}^{2} \\[ 5pt ] &=&3\times 0.8\times 170.88^{2}+3\times 1.6\times 80^{2} \\[ 5pt ] &≒&70 \ 080+30 \ 720 \\[ 5pt ] &≒&100 \ 800 \ \mathrm {[W]}　→　101 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] となるので，進相コンデンサを接続することで，線路損失は\( \ 43 \ \mathrm {[kW]} \ \)減少する。