《電力・管理》〈送電〉[H21:問6]受電用遮断器を通過する三相短絡電流に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

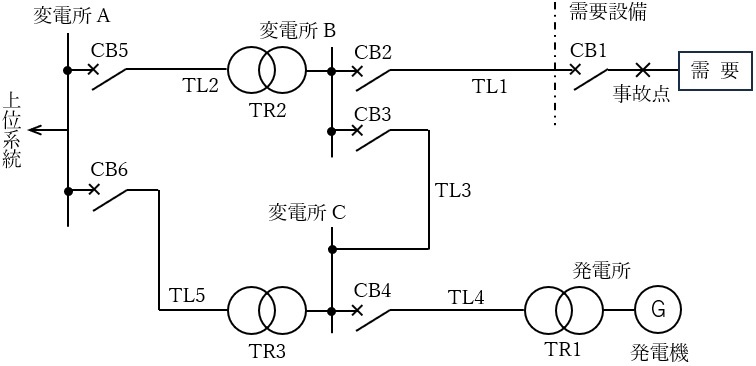
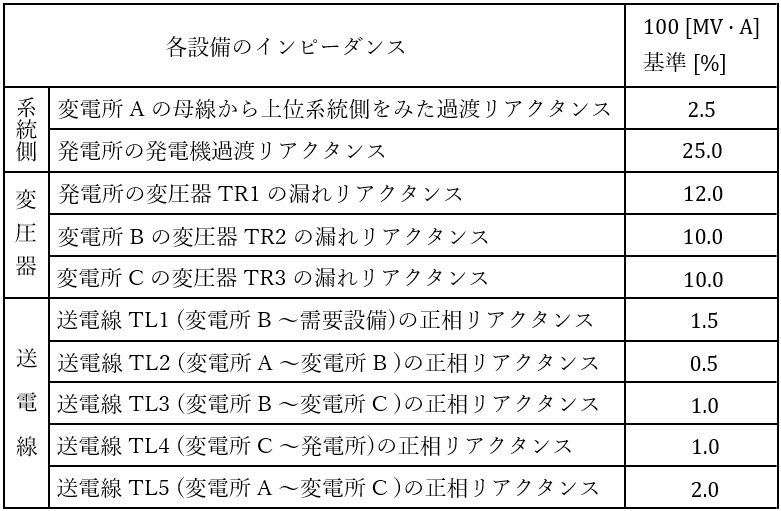
図の特別高圧系統から電圧\( \ 66 \ \mathrm {[kV]} \ \)で受電している需要設備における，受電用遮断器\( \ \mathrm {\left( CB1\right) } \ \)を通過する短絡電流について，次の問に答えよ。ただし，発電機，変圧器及び送電線のインピーダンスは，表に示すとおりである。また，短絡電流の計算において，発電機，変圧器及び送電線の抵抗分，もしくは変圧器の励磁インピーダンスは無視できるものとし，短絡時における上位系統及び発電機の過渡リアクタンスの背後電圧は\( \ 1.0 \ \mathrm {[p.u.]} \ \)であるとする。

(1)　\( \ \mathrm {CB1} \ \)，\( \ \mathrm {CB2} \ \)，\( \ \mathrm {CB4} \ \)，\( \ \mathrm {CB5} \ \)及び\( \ \mathrm {CB6} \ \)が閉のとき，事故点における三相短絡電流\( \ \mathrm {[kA]} \ \)を求めよ。

(2)　上記(1)の状態において，変電所\( \ \mathrm {B} \ \)と変電所\( \ \mathrm {C} \ \)を連系する\( \ \mathrm {CB3} \ \)を閉としたとき，事故点における三相短絡電流\( \ \mathrm {[kA]} \ \)を求めよ。

【ワンポイント解説】

事故点で発生する三相短絡電流を求める問題です。
回路演算がやや複雑になりますが，考え方はそれほど難しくありません。
計算間違いに十分注意して，完答を目指すようにして下さい。

1.オーム法からパーセントインピーダンス法への変換
基準容量を\( \ P_{\mathrm {n}} \ \mathrm {[V\cdot A]} \ \)，基準電圧を\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \)，基準電流を\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)とすると，\( \ Z \ \mathrm {[\Omega ]} \ \)の百分率インピーダンス（パーセントインピーダンス）\( \ ％Z \ \mathrm {[％]} \ \)は，
\[
\begin{eqnarray}
％Z&=&\frac {ZI_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}\times 100 　(定義) \\[ 5pt ] &=&\frac {\sqrt {3}ZI_{\mathrm {n}}}{V_{\mathrm {n}}}\times 100 \\[ 5pt ] &=&\frac {\sqrt {3}ZV_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}}\times 100 \\[ 5pt ] &=&\frac {P_{\mathrm {n}}Z}{V_{\mathrm {n}}^{2}}\times 100　　 (∵P_{\mathrm {n}}=\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} ) \\[ 5pt ] \end{eqnarray}
\] となります。

2.百分率インピーダンスの短絡電流計算
ある地点から電源側を見た百分率インピーダンスを\( \ ％Z \ \mathrm {[％]} \ \)とすると，その点での三相短絡電流\( \ I_{\mathrm {s}} \ \mathrm {[A]} \ \)は，基準電流\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)を用いて，
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {I_{\mathrm {n}}}{％Z／100} \\[ 5pt ] &=&\frac {100I_{\mathrm {n}}}{％Z} \\[ 5pt ] \end{eqnarray}
\] で求められます。

※百分率インピーダンスの定義式等を用いて\( \ \displaystyle I_{\mathrm {s}}=\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}} \ \)から上式を求めることはできますが，試験時には暗記しておいた方が良いと思います。
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}{Z_{\mathrm {s}} \ \mathrm {[\Omega ]}} \\[ 5pt ] &=&\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}} \\[ 5pt ] &=&\frac {V_{\mathrm {n}}I_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}I_{\mathrm {n}}} \\[ 5pt ] &=&\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}I_{\mathrm {n}}}\times I_{\mathrm {n}} \\[ 5pt ] &=&\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}I_{\mathrm {n}}\times 100}\times 100I_{\mathrm {n}} \\[ 5pt ] &=&\frac {100I_{\mathrm {n}}}{％Z_{\mathrm {s}}} \\[ 5pt ] \end{eqnarray}
\]

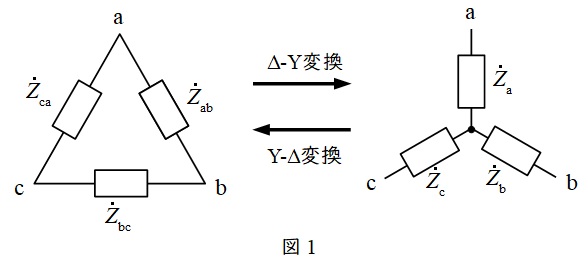
3.\( \ \Delta -\mathrm {Y} \ \)変換と\( \ \mathrm {Y}-\Delta \ \)変換
①\( \ \Delta -\mathrm {Y} \ \)変換
図1において，
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {a}}&=&\frac {{\dot Z}_{\mathrm {ab}}{\dot Z}_{\mathrm {ca}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ] {\dot Z}_{\mathrm {b}}&=&\frac {{\dot Z}_{\mathrm {bc}}{\dot Z}_{\mathrm {ab}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ] {\dot Z}_{\mathrm {c}}&=&\frac {{\dot Z}_{\mathrm {ca}}{\dot Z}_{\mathrm {bc}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ] \end{eqnarray}
\] ②\( \ \mathrm {Y}-\Delta \ \)変換
図1において，
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {ab}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {c}}} \\[ 5pt ] {\dot Z}_{\mathrm {bc}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {a}}} \\[ 5pt ] {\dot Z}_{\mathrm {ca}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {b}}} \\[ 5pt ] \end{eqnarray}
\] 平衡三相回路においては，
\[
{\dot Z}_{\mathrm {ab}}={\dot Z}_{\mathrm {bc}}={\dot Z}_{\mathrm {ca}}=3{\dot Z}_{\mathrm {a}}=3{\dot Z}_{\mathrm {b}}=3{\dot Z}_{\mathrm {c}}
\] となります。

【解答】

(1)\( \ \mathrm {CB1} \ \)，\( \ \mathrm {CB2} \ \)，\( \ \mathrm {CB4} \ \)，\( \ \mathrm {CB5} \ \)及び\( \ \mathrm {CB6} \ \)が閉のとき，事故点における三相短絡電流\( \ \mathrm {[kA]} \ \)
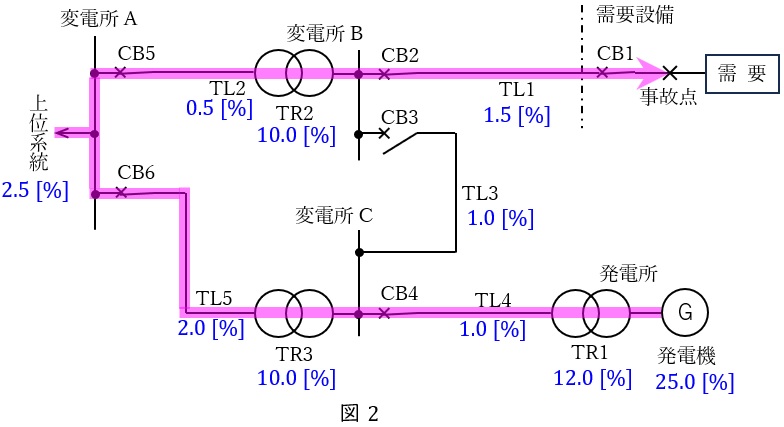
問題図に表に記載のあるインピーダンスを記載し，\( \ \mathrm {CB1} \ \)，\( \ \mathrm {CB2} \ \)，\( \ \mathrm {CB4} \ \)，\( \ \mathrm {CB5} \ \)及び\( \ \mathrm {CB6} \ \)が閉のときの事故発生時の様子は図2に示す通りとなる。
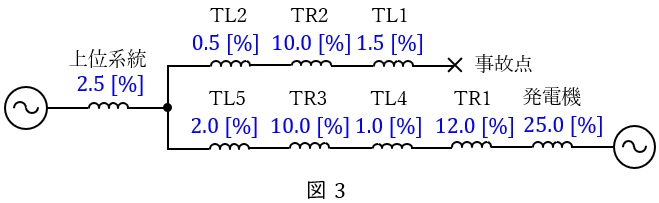
図2に示すように，事故発生時は事故点に向かい上位系統及び発電機から電流が流れるので，事故点から見た等価回路は図3のようになる。
したがって，事故点から電源側を見た合成インピーダンス\( \ ％Z \ \mathrm {[％]} \ \)は，
\[
\begin{eqnarray}
％Z&=&1.5+10.0+0.5+\frac {2.5\times \left( 2.0+10.0+1.0+12.0+25.0\right) }{2.5+\left( 2.0+10.0+1.0+12.0+25.0\right) } \\[ 5pt ] &≒&1.5+10.0+0.5+2.3810 \\[ 5pt ] &≒&14.381 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] となる。また，定格電流\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)は，定格容量\( \ P_{\mathrm {n}}=100 \ \mathrm {[MV\cdot A]} \ \)及び定格電圧\( \ V_{\mathrm {n}}=66 \ \mathrm {[kV]} \ \)より，
\[
\begin{eqnarray}
I_{\mathrm {n}}&=&\frac {P_{\mathrm {n}}}{\sqrt {3}V_{\mathrm {n}}} \\[ 5pt ] &=&\frac {100\times 10^{6}}{\sqrt {3}\times 66\times 10^{3}} \\[ 5pt ] &≒&874.77 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] であるので，三相短絡電流\( \ I_{\mathrm {s}} \ \mathrm {[kA]} \ \)は，ワンポイント解説「2.百分率インピーダンスの短絡電流計算」の通り，
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {100I_{\mathrm {n}}}{％Z} \\[ 5pt ] &=&\frac {100\times 874.77}{14.381} \\[ 5pt ] &≒&6 \ 082.8 \ \mathrm {[A]}　→　6.08 \ \mathrm {[kA]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)さらに\( \ \mathrm {CB3} \ \)を閉としたとき，事故点における三相短絡電流\( \ \mathrm {[kA]} \ \)
(1)の状態から\( \ \mathrm {CB3} \ \)を閉としたときの事故発生時は図4のようになり，事故点から見た等価回路は図5のようになる。

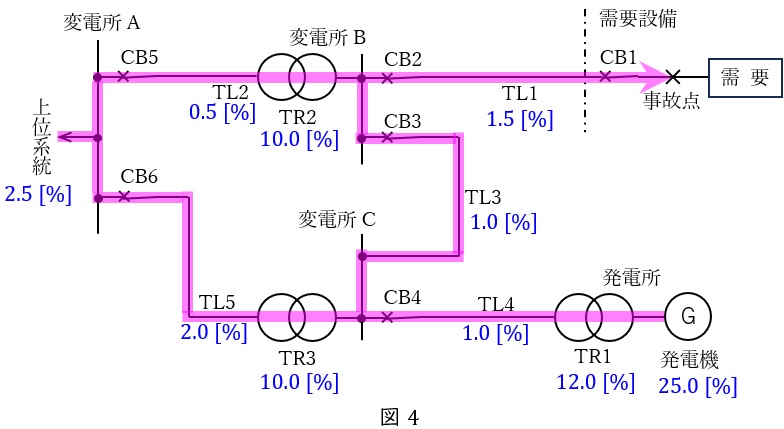
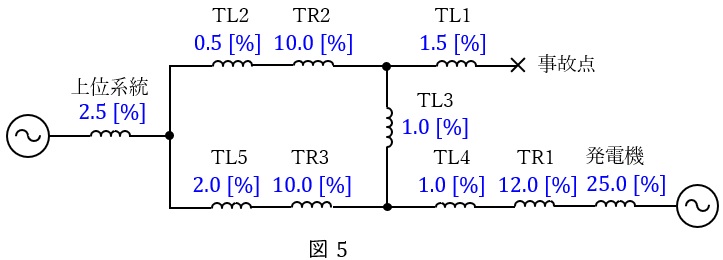
図5において，\( \ \mathrm {TL2} \ \)，\( \ \mathrm {TR2} \ \)，\( \ \mathrm {TL3} \ \)，\( \ \mathrm {TL5} \ \)，\( \ \mathrm {TR3} \ \)で構成される\( \ \Delta \ \)回路について\( \ \Delta -\mathrm {Y} \ \)変換すると各インピーダンスは，ワンポイント解説「3.\( \ \Delta -\mathrm {Y} \ \)変換と\( \ \mathrm {Y}-\Delta \ \)変換」の通り，
\[
\begin{eqnarray}
\frac {\left( 0.5+10.0\right) \times 1.0}{\left( 0.5+10.0\right) +1.0+\left( 2.0+10.0\right) }&≒&0.44681 \\[ 5pt ] \frac {1.0\times \left( 2.0+10.0\right) }{\left( 0.5+10.0\right) +1.0+\left( 2.0+10.0\right) }&≒&0.51064 \\[ 5pt ] \frac {\left( 2.0+10.0\right) \times \left( 0.5+10.0\right) }{\left( 0.5+10.0\right) +1.0+\left( 2.0+10.0\right) }&≒&5.3617 \\[ 5pt ] \end{eqnarray}
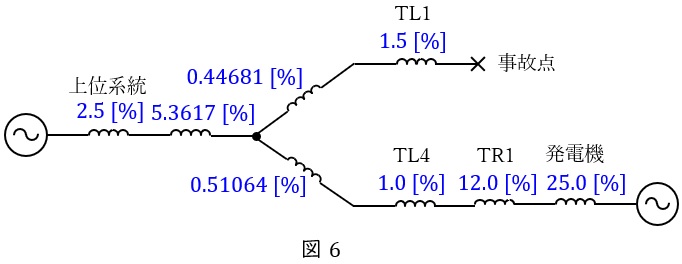
\] となるので，図6のように書き換えられる。したがって，事故点からみた合成インピーダンス\( \ ％Z^{\prime } \ \mathrm {[％]} \ \)は，
\[
\begin{eqnarray}
％Z^{\prime }&=&1.5+0.44681+\frac {\left( 5.3617+2.5\right) \times \left( 0.51064+1.0+12.0+25.0\right) }{\left( 5.3617+2.5\right) +\left( 0.51064+1.0+12.0+25.0\right) } \\[ 5pt ] &≒&1.5+0.44681+6.5289 \\[ 5pt ] &≒&8.4757 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] となるので，三相短絡電流\( \ I_{\mathrm {s}}^{\prime } \ \mathrm {[kA]} \ \)は，ワンポイント解説「2.百分率インピーダンスの短絡電流計算」の通り，
\[
\begin{eqnarray}
I_{\mathrm {s}}^{\prime }&=&\frac {100I_{\mathrm {n}}}{％Z^{\prime }} \\[ 5pt ] &=&\frac {100\times 874.77}{8.4757} \\[ 5pt ] &≒&10 \ 321 \ \mathrm {[A]}　→　10.3 \ \mathrm {[kA]} \\[ 5pt ] \end{eqnarray}
\] と求められる。