《電力・管理》〈送電〉[H23:問3]変圧器を含む送電線路の電力に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

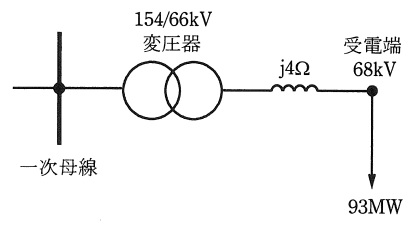
図のような三相\( \ 3 \ \)線式の\( \ 1 \ \)回線送電線路がある。変圧器の定格電圧は一次側\( \ 154 \ \mathrm {[kV]} \ \)，二次側\( \ 66 \ \mathrm {[kV]} \ \)，定格容量は\( \ 200 \ \mathrm {[MV\cdot A]} \ \)であり，一次・二次間は\( \ \mathrm {Y – Y} \ \)で結線されている。変圧器のインピーダンスはリアクタンスのみとし，その値は自己容量ベースで\( \ 15 \ \mathrm {[％]} \ \)とする。送電線路のインピーダンスは\( \ \mathrm {j}4 \ \mathrm {[\Omega ]} \ \)とし，その他のインピーダンスは無視できるものとする。その送電線路の受電端に有効電力が\( \ 93 \ \mathrm {[MW]} \ \)（力率は不明）の負荷を接続したときに，受電端電圧が\( \ 68 \ \mathrm {[kV]} \ \)となった。また，一次母線と受電端との位相差\( \ \delta \ \)\(\displaystyle \left( 0 \lt \delta \lt \frac {\pi }{2}\right) \)については，\( \ \sin \delta =0.15 \ \)となった。このとき，次の問に答えよ。

(1)　変圧器のインピーダンスを変圧器二次側換算値\( \ \mathrm {[\Omega ]} \ \)で答えよ。

(2)　一次母線の電圧\( \ \mathrm {[kV]} \ \)，及び負荷の消費する無効電力\( \ \mathrm {[Mvar]} \ \)を求めよ。ただし，無効電力の符号は遅れを正とする。

(3)　ある容量の調相設備（分路リアクトルもしくは電力用コンデンサ）を受電端に並列接続すると，受電端電圧が\( \ 66 \ \mathrm {[kV]} \ \)に低下した。受電端に接続した調相設備の種類及び容量\( \ \mathrm {[MV\cdot A]} \ \)を答えよ。ただし，一次母線の電圧は一定とし，負荷は電圧によらず定電力特性を持つものとする。

【ワンポイント解説】

受電端の電力と電圧に関する問題です。
変圧器がなければ標準的な問題となりますが，変圧器が絡むことで少し計算量が増え難易度が高くなっています。

1.オーム法からパーセントインピーダンス法への変換
基準容量を\( \ P_{\mathrm {n}} \ \)，基準電圧を\( \ V_{\mathrm {n}} \ \)，基準電流を\( \ I_{\mathrm {n}} \ \)とすると，
\[
\begin{eqnarray}
％Z&=&\frac {ZI_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}\times 100　　 (定義) \\[ 5pt ] &=&\frac {\sqrt {3}ZI_{\mathrm {n}}}{V_{\mathrm {n}}}\times 100 \\[ 5pt ] &=&\frac {\sqrt {3}ZV_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}}\times 100 \\[ 5pt ] &=&\frac {P_{\mathrm {n}}Z}{V_{\mathrm {n}}^{2}}\times 100　　 (∵P_{\mathrm {n}}=\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} ) \\[ 5pt ] \end{eqnarray}
\] となります。

2.オイラーの公式
極座標空間において，
\[
\begin{eqnarray}
\mathrm {e}^{\mathrm {j}\theta }&=&\cos \theta +\mathrm {j}\sin \theta \\[ 5pt ] \end{eqnarray}
\] となり，これをオイラーの公式といいます。したがって，\( \ {\dot V}_{\mathrm {s}}= V_{\mathrm {s}}∠\delta \ \)，\( \ {\dot V}_{\mathrm {r}}= V_{\mathrm {r}}∠0 \ \)は，
\[
\begin{eqnarray}
{\dot V}_{\mathrm {s}}&=&V_{\mathrm {s}}\left( \cos \delta +\mathrm {j}\sin \delta \right) \\[ 5pt ] {\dot V}_{\mathrm {r}}&=&V_{\mathrm {r}} \\[ 5pt ] \end{eqnarray}
\] と表すことができます。

3.有効電力と無効電力の公式
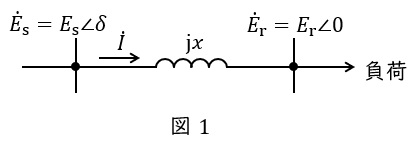
図1に示すような系統について，送電端電圧（相電圧）\( \ {\dot E}_{\mathrm {s}}= E_{\mathrm {s}}∠\delta \ \)と受電端電圧（相電圧）\( \ {\dot E}_{\mathrm {r}}= E_{\mathrm {r}}∠0 \ \)の関係は，
\[
\begin{eqnarray}
{\dot E}_{\mathrm {s}}&=&{\dot E}_{\mathrm {r}}+\mathrm {j}x{\dot I} \\[ 5pt ] \end{eqnarray}
\] となります。オイラーの公式より，
\[
\begin{eqnarray}
E_{\mathrm {s}}\left( \cos \delta +\mathrm {j}\sin \delta \right) &=&E_{\mathrm {r}}+\mathrm {j}x{\dot I} \\[ 5pt ] \mathrm {j}x{\dot I}&=&E_{\mathrm {s}}\left( \cos \delta +\mathrm {j}\sin \delta \right) -E_{\mathrm {r}} \\[ 5pt ] \dot I&=&\frac {E_{\mathrm {s}}\left( \cos \delta +\mathrm {j}\sin \delta \right) -E_{\mathrm {r}}}{\mathrm {j}x} \\[ 5pt ] &=&\frac {E_{\mathrm {s}}\sin \delta }{x}-\mathrm {j}\frac {E_{\mathrm {s}}\cos \delta -E_{\mathrm {r}}}{x} \\[ 5pt ] \end{eqnarray}
\] となるので，送電端から受電端への送電電力\( \ P+\mathrm {j}Q \ \)は遅れ無効電力を正とすると，
\[
\begin{eqnarray}
P+\mathrm {j}Q&=&3{\dot E}_{\mathrm {r}}\overline {\dot I} \\[ 5pt ] &=&3E_{\mathrm {r}}\left( \frac {E_{\mathrm {s}}\sin \delta }{x}+\mathrm {j}\frac {E_{\mathrm {s}}\cos \delta -E_{\mathrm {r}}}{x}\right) \\[ 5pt ] &=&\frac {3E_{\mathrm {s}}E_{\mathrm {r}}\sin \delta }{x} +\mathrm {j}\frac {3E_{\mathrm {s}}E_{\mathrm {r}}\cos \delta -3E_{\mathrm {r}}^{2}}{x} \\[ 5pt ] \end{eqnarray}
\] となり，線間電圧\( \ V_{\mathrm {s}}=\sqrt {3}E_{\mathrm {s}} \ \)及び\( \ V_{\mathrm {r}}=\sqrt {3}E_{\mathrm {r}} \ \)を用いて表せば，
\[
\begin{eqnarray}
P+\mathrm {j}Q&=&\frac {V_{\mathrm {s}}V_{\mathrm {r}}\sin \delta }{x} +\mathrm {j}\frac {V_{\mathrm {s}}V_{\mathrm {r}}\cos \delta -V_{\mathrm {r}}^{2}}{x} \\[ 5pt ] \end{eqnarray}
\] となります。実数部と虚数部を比較すると，
\[
\begin{eqnarray}
P&=&\frac {V_{\mathrm {s}}V_{\mathrm {r}}\sin \delta }{x} \\[ 5pt ] Q&=&\frac {V_{\mathrm {s}}V_{\mathrm {r}}\cos \delta -V_{\mathrm {r}}^{2}}{x} \\[ 5pt ] \end{eqnarray}
\] と求められます。

※　これは公式として覚えておいて良いですが，導出できるようにしておきましょう。

【解答】

(1)変圧器のインピーダンスの二次側換算値\( \ \mathrm {[\Omega ]} \ \)
ワンポイント解説「1.オーム法からパーセントインピーダンス法への変換」より，変圧器のインピーダンス\( \ x_{\mathrm {T}} \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
％x_{\mathrm {T}}&=&\frac {P_{\mathrm {n}}x_{\mathrm {T}}}{V_{\mathrm {n}}^{2}}\times 100 \\[ 5pt ] x_{\mathrm {T}}&=&\frac {V_{\mathrm {n}}^{2}％x_{\mathrm {T}}}{100P_{\mathrm {n}}} \\[ 5pt ] &=&\frac {\left( 66\times 10^{3}\right) ^{2}\times 15}{100\times \left( 200\times 10^{6}\right) } \\[ 5pt ] &=&3.267　→　3.27 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)一次母線の電圧\( \ \mathrm {[kV]} \ \)，及び負荷の消費する無効電力\( \ \mathrm {[Mvar]} \ \)
送電線路のインピーダンス\( \ \mathrm {j}x= \mathrm {j}4 \ \mathrm {[\Omega ]} \ \)より，一次母線の電圧の二次側換算\( \ V_{\mathrm {s}}^{\prime } \ \mathrm {[kV]} \ \)は，ワンポイント解説「3.有効電力と無効電力の公式」より，
\[
\begin{eqnarray}
P&=&\frac {V_{\mathrm {s}}^{\prime }V_{\mathrm {r}}\sin \delta }{x_{\mathrm {T}}+x} \\[ 5pt ] V_{\mathrm {s}}^{\prime }&=&\frac {P\left( x_{\mathrm {T}}+x\right) }{V_{\mathrm {r}}\sin \delta } \\[ 5pt ] &=&\frac {93\times 10^{6}\times \left( 3.267+4\right) }{68\times 10^{3}\times 0.15 } \\[ 5pt ] &≒&66.258\times 10^{3} \ \mathrm {[V]}　→　66.258 \ \mathrm {[kV]} \\[ 5pt ] \end{eqnarray}
\] となるので，一次母線の電圧\( \ V_{\mathrm {s}} \ \mathrm {[kV]} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {s}}&=&\frac {154}{66}\times V_{\mathrm {s}}^{\prime } \\[ 5pt ] &=&\frac {154}{66}\times 66.258 \\[ 5pt ] &≒&154.60　→　155 \ \mathrm {[kV]} \\[ 5pt ] \end{eqnarray}
\] と求められる。また，無効電力\( \ Q \ \mathrm {[Mvar]} \ \)は，ワンポイント解説「3.有効電力と無効電力の公式」より，
\[
\begin{eqnarray}
Q&=&\frac {V_{\mathrm {s}}^{\prime }V_{\mathrm {r}}\cos \delta -V_{\mathrm {r}}^{2}}{x_{\mathrm {T}}+x} \\[ 5pt ] &=&\frac {V_{\mathrm {s}}^{\prime }V_{\mathrm {r}}\sqrt {1-\sin ^{2}\delta }-V_{\mathrm {r}}^{2}}{x_{\mathrm {T}}+x} \\[ 5pt ] &=&\frac {\left( 66.258\times 10^{3}\right) \times \left( 68\times 10^{3}\right) \times \sqrt {1-0.15 ^{2} } -\left( 68\times 10^{3}\right) ^{2}}{3.267+4} \\[ 5pt ] &≒&-23.315\times 10^{6} \ \mathrm {[var]}　→　-23.3 \ \mathrm {[Mvar]} \\[ 5pt ] \end{eqnarray}
\] となり，\( \ 23.3 \ \mathrm {[Mvar]} \ \)の進み電力と求められる。

(3)受電端電圧が\( \ 66 \ \mathrm {[kV]} \ \)に低下したときの，受電端に接続した調相設備の種類及び容量\( \ \mathrm {[MV\cdot A]} \ \)
本問の条件において，受電端電圧が\( \ V_{\mathrm {r}}^{\prime }=66 \ \mathrm {[kV]} \ \)に低下したとき，一次母線の電圧\( \ V_{\mathrm {s}} \ \mathrm {[kV]} \ \)，有効電力\( \ P \ \mathrm {[MW]} \ \)には変化がないから，変化後の位相差\( \ \delta ^{\prime } \ \)の正弦\( \ \sin \delta ^{\prime } \ \)は，
\[
\begin{eqnarray}
P&=&\frac {V_{\mathrm {s}}^{\prime }V_{\mathrm {r}}^{\prime }\sin \delta ^{\prime } }{x_{\mathrm {T}}+x} \\[ 5pt ] \sin \delta ^{\prime } &=&\frac {P\left( x_{\mathrm {T}}+x\right) }{V_{\mathrm {s}}^{\prime }V_{\mathrm {r}}^{\prime }} \\[ 5pt ] &=&\frac {93\times 10^{6}\times \left( 3.267+4\right) }{\left( 66.258\times 10^{3}\right) \times \left( 66\times 10^{3}\right) } \\[ 5pt ] &≒&0.15455 \\[ 5pt ] \end{eqnarray}
\] となるので，このときの無効電力\( \ Q^{\prime } \ \mathrm {[Mvar]} \ \)は，
\[
\begin{eqnarray}
Q^{\prime }&=&\frac {V_{\mathrm {s}}^{\prime }V_{\mathrm {r}}^{\prime }\cos \delta ^{\prime }-{V_{\mathrm {r}}^{\prime }}^{2}}{x_{\mathrm {T}}+x} \\[ 5pt ] &=&\frac {V_{\mathrm {s}}^{\prime }V_{\mathrm {r}}^{\prime }\sqrt {1-\sin ^{2}\delta ^{\prime }}-{V_{\mathrm {r}}^{\prime }}^{2}}{x_{\mathrm {T}}+x} \\[ 5pt ] &=&\frac {\left( 66.258\times 10^{3}\right) \times \left( 66\times 10^{3}\right) \times \sqrt {1-0.15455 ^{2} } -\left( 66\times 10^{3}\right) ^{2}}{3.267+4} \\[ 5pt ] &≒&-4.8870\times 10^{6} \ \mathrm {[var]}　→　-4.8870 \ \mathrm {[Mvar]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，調相設備の電力\( \ Q_{\mathrm {P}} \ \mathrm {[Mvar]} \ \)は，
\[
\begin{eqnarray}
Q_{\mathrm {P}}&=&Q^{\prime }-Q \\[ 5pt ] &=&-4.8870-\left( -23.315\right) \\[ 5pt ] &≒&18.428　→　18.4 \ \mathrm {[Mvar]} \\[ 5pt ] \end{eqnarray}
\] となるので，調相設備は分路リアクトルで容量は\( \ 18.4 \ \mathrm {[Mvar]} \ \)と求められる。