《電力・管理》〈配電〉[H23:問4]異容量三相4線式配電方式に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

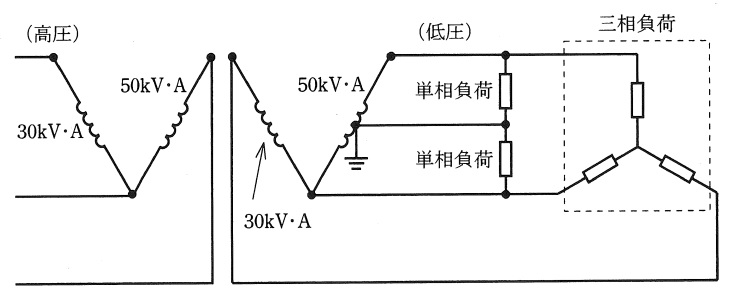
図のように，定格容量\( \ 30 \ \mathrm {[kV\cdot A]} \ \)及び\( \ 50 \ \mathrm {[kV\cdot A]} \ \)の変圧器を異容量\( \ \mathrm {V} \ \)結線とした対称三相交流電源がある。低圧側にまず三相の最大平衡負荷を接続し，次に単相負荷を図のように接続して，変圧器の利用率（負荷の合計／変圧器の定格容量の合計）を最大とする。このとき，次の値を求めよ。ただし，変圧器及び線路のインピーダンスは無視するものとする。

(1)　三相の最大平衡負荷　\( \ \mathrm {[kW]} \ \)

(2)　単相負荷の合計　\( \ \mathrm {[kW]} \ \)

(3)　変圧器の利用率　\( \ \mathrm {[％]} \ \)

【ワンポイント解説】

異容量\( \ \mathrm {V} \ \)結線での電力計算に関する問題です。
いきなり図3のベクトル図を見るとわけがわからないかもしれませんが，三相負荷の電圧と電流→専用変圧器の電流→共用変圧器及び専用変圧器の電圧→単相負荷の電圧と電流→共用変圧器の電流という順に整理していけば理解ができるかと思います。

1.三相\( \ 4 \ \)線式異容量\( \ \mathrm {V} \ \)結線
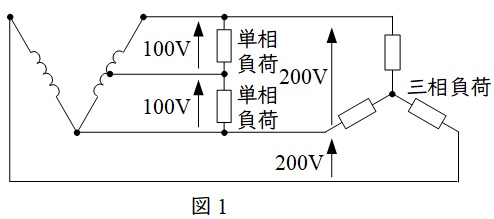
電灯の\( \ 100 \ \mathrm {[V]} \ \)と動力の\( \ 200 \ \mathrm {[V]} \ \)の両方に供給することが可能な配電方式です。
単相負荷と三相負荷の両方に供給する変圧器を共用変圧器，三相負荷のみに供給する変圧器を専用変圧器といいます。
単相負荷の分だけ共用変圧器の方が容量が多く必要とするので，異容量\( \ \mathrm {V} \ \)結線といいます。

【解答】

(1)三相の最大平衡負荷\( \ \mathrm {[kW]} \ \)
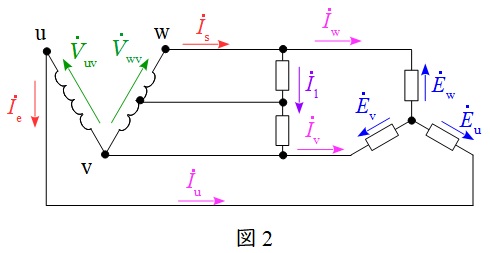
低圧側の各端子，電圧及び電流を図2のようにおく。
三相負荷が平衡負荷である場合，その電力\( \ P_{\mathrm {3}} \ \mathrm {[kW]} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {3}}&=&3E_{\mathrm {u}}I_{\mathrm {u}}\cos \phi \\[ 5pt ] &=&3\cdot \frac {V_{\mathrm {uv}}}{\sqrt {3}}I_{\mathrm {u}}\cos \phi \\[ 5pt ] &=&\sqrt {3}V_{\mathrm {uv}}I_{\mathrm {u}}\cos \phi \\[ 5pt ] \end{eqnarray}
\] で求められ，専用変圧器の容量\( \ S_{\mathrm {e}}=V_{\mathrm {uv}}I_{\mathrm {u}}=30 \ \mathrm {[kV\cdot A]} \ \)で力率\( \ \cos \phi \ \)の最大値は\( \ 1 \ \)であるから，最大平衡負荷\( \ P_{\mathrm {3m}} \ \mathrm {[kW]} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {3m}}&=&\sqrt {3}\times 30 \times 1 \\[ 5pt ] &≒&51.961　→　52.0 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)単相負荷の合計\( \ \mathrm {[kW]} \ \)
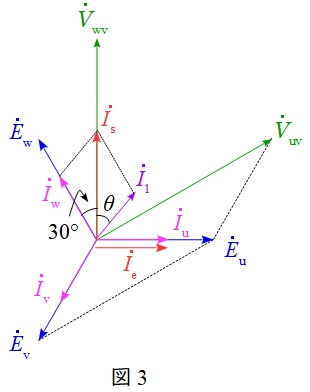
最大平衡負荷を接続し，変圧器の利用率を最大にしたときのベクトル図を図3に示す。
共用変圧器の利用率を最大とするためには，\( \ {\dot V}_{\mathrm {wv}} \ \)と\( \ {\dot I}_{\mathrm {s}} \ \)が同相である必要がある。したがって，このときの単相負荷の合計容量を\( \ P_{\mathrm {1m}}
\ \mathrm {[kW]} \ \)とすると，
\[
\begin{eqnarray}
V_{\mathrm {wv}}I_{\mathrm {s}}&=&V_{\mathrm {wv}}I_{\mathrm {w}}\cos 30°+P_{\mathrm {1m}} \\[ 5pt ] &=&\frac {\sqrt {3}}{2}V_{\mathrm {wv}}I_{\mathrm {w}}+P_{\mathrm {1m}} \\[ 5pt ] \end{eqnarray}
\] の関係があり，共用変圧器の容量が\( \ S_{\mathrm {s}}=V_{\mathrm {wv}}I_{\mathrm {s}}=50 \ \mathrm {[kV\cdot A]} \ \)であることから，
\[
\begin{eqnarray}
50&=&\frac {\sqrt {3}}{2}\times 30+P_{\mathrm {1m}} \\[ 5pt ] P_{\mathrm {1m}} &≒&24.019　→　24.0 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)変圧器の利用率\( \ \mathrm {[％]} \ \)
(1)，(2)より，変圧器の利用率\( \ \alpha \ \mathrm {[％]} \ \)は，
\[
\begin{eqnarray}
\alpha &=&\frac {P_{\mathrm {3m}}+P_{\mathrm {1m}}}{S_{\mathrm {e}}+S_{\mathrm {s}}}\times 100 \\[ 5pt ] &=&\frac {51.961+24.019}{30+50}\times 100 \\[ 5pt ] &≒&94.975　→　95.0 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。