《電力・管理》〈変電〉[H24:問5]電力系統の変電所での電圧調整に関する計算問題

【問題】

【難易度】★☆☆☆☆（易しい）

電力系統の変電所での電圧調整について，次の問に答えなさい。

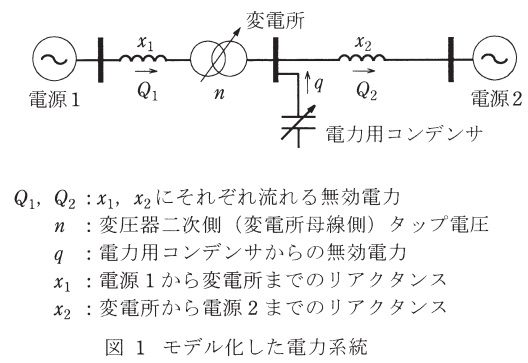
図1のようにモデル化した電力系統において，電源\( \ 1 \ \)と電源\( \ 2 \ \)の電圧がそれぞれ一定であるとき，変圧器二次側（変電所母線側）タップ電圧（以下，変圧器タップ電圧）の微少調整量を\( \ \mathit {\Delta } n \ \)，電力用コンデンサからの無効電力の微少調整量を\( \ \mathit {\Delta } q \ \)とおけば，これらの調整による変電所の電圧の微少変化量\( \ \mathit {\Delta } V \ \)は近似的に，単位法で示すと
\[
\begin{eqnarray}
\mathit {\Delta } V&=&A_{\mathrm {n}}\cdot \mathit {\Delta } n +A_{\mathrm {q}}\cdot \mathit {\Delta } q \\[ 5pt ] \end{eqnarray}
\] と表すことができる。この式の係数\( \ A_{\mathrm {n}} \ \)，\( \ A_{\mathrm {q}} \ \)を次のようにして求めることができる。

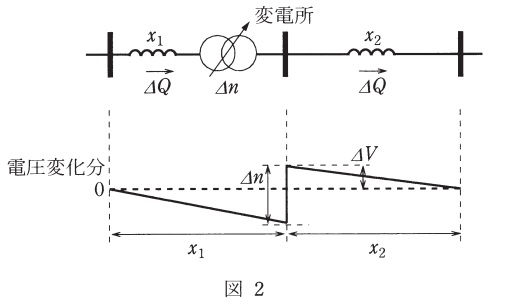
(1)　電力用コンデンサからの無効電力調整を行わない\( \ \left( \mathit {\Delta } q =0 \right) \ \)の場合，変圧器タップ電圧を\( \ \mathit {\Delta } n \ \)調整したときの電圧変化の分布は図2のようになる。変圧器のタップ調整にともない線路の無効電力潮流は\( \ \mathit {\Delta } Q \ \)変化するものとした場合，係数\( \ A_{\mathrm {n}} \ \)を\( \ x_{\mathrm {1}} \ \)及び\( \ x_{\mathrm {2}} \ \)で表しなさい。

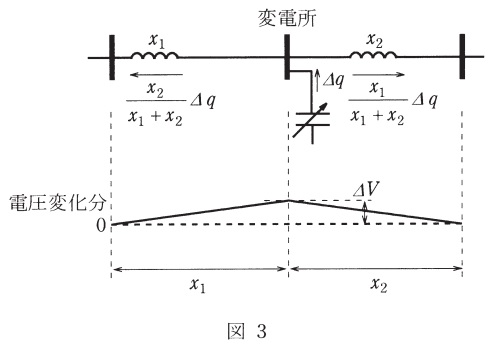
(2)　変圧器のタップ調整を行わない\( \ \left( \mathit {\Delta } n =0 \right) \ \)の場合，電力用コンデンサからの無効電力を\( \ \mathit {\Delta } q \ \)調整したときの電圧変化の分布は図3のようになる。線路の無効電力潮流は，\( \ \mathit {\Delta } q \ \)が線路リアクタンスの逆比で分流した分だけそれぞれ変化するものとした場合，係数\( \ A_{\mathrm {q}} \ \)を\( \ x_{\mathrm {1}} \ \)及び\( \ x_{\mathrm {2}} \ \)で表しなさい。

なお，モデル系統における上記の計算において，リアクタンス\( \ x \ \)を通る無効電力潮流が\( \ \mathit {\Delta } Q \ \)変化したときの変電所の電圧変化\( \ \mathit {\Delta } V \ \)は近似的に，単位法で示すと
\[
\begin{eqnarray}
\mathit {\Delta } V&=&x\cdot \mathit {\Delta } Q \\[ 5pt ] \end{eqnarray}
\] で表されるものとする。

【ワンポイント解説】

変電所における電圧調整に関する問題です。
問題の内容が理解できれば，特別な公式は不要な非常に易しい問題ですが，逆に問題の内容が理解できなければ全くわからない問題となってしまいます。
二次試験では本問のように，受験生でその場で考えさせるような問題が出題されることがあります。見たことないからと諦めず，粘り強く取り組めるかが合否の分かれ目となります。

【解答】

(1)係数\( \ A_{\mathrm {n}} \ \)を\( \ x_{\mathrm {1}} \ \)及び\( \ x_{\mathrm {2}} \ \)で表す
図2より，\( \ x_{\mathrm {2}} \ \)における電圧変化\( \ \mathit {\Delta } V \ \)は，近似的に表すと，
\[
\begin{eqnarray}
\mathit {\Delta } V&=&x_{\mathrm {2}}\cdot \mathit {\Delta } Q \ 　・・・・・・・・・・・・・　① \\[ 5pt ] \end{eqnarray}
\] であり，\( \ x_{\mathrm {1}} \ \)と\( \ x_{\mathrm {2}} \ \)を合わせた電圧変化\( \ \mathit {\Delta } n \ \)は，
\[
\begin{eqnarray}
\mathit {\Delta } n&=&x_{\mathrm {1}}\cdot \mathit {\Delta } Q+x_{\mathrm {2}}\cdot \mathit {\Delta } Q \\[ 5pt ] &=&\left( x_{\mathrm {1}}+x_{\mathrm {2}}\right) \cdot \mathit {\Delta } Q　・・・・・・・・・・　② \\[ 5pt ] \end{eqnarray}
\] となる。題意より，電力用コンデンサからの無効電力調整は行わない\( \ \left( \mathit {\Delta } q =0 \right) \ \)ので，変電所の電圧の微少変化量\( \ \mathit {\Delta } V \ \)と変圧器二次側タップ電圧（以下，変圧器タップ電圧）の微少調整量\( \ \mathit {\Delta } n \ \)の関係を表すと，
\[
\begin{eqnarray}
\mathit {\Delta } V&=&A_{\mathrm {n}}\cdot \mathit {\Delta } n \\[ 5pt ] \end{eqnarray}
\] となるので，上式に①及び②を代入すると，
\[
\begin{eqnarray}
x_{\mathrm {2}}\cdot \mathit {\Delta } Q&=&A_{\mathrm {n}}\cdot \left( x_{\mathrm {1}}+x_{\mathrm {2}}\right) \cdot \mathit {\Delta } Q \\[ 5pt ] x_{\mathrm {2}}&=&A_{\mathrm {n}}\cdot \left( x_{\mathrm {1}}+x_{\mathrm {2}}\right) \\[ 5pt ] A_{\mathrm {n}}&=&\frac {x_{\mathrm {2}}}{x_{\mathrm {1}}+x_{\mathrm {2}}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)係数\( \ A_{\mathrm {q}} \ \)を\( \ x_{\mathrm {1}} \ \)及び\( \ x_{\mathrm {2}} \ \)で表す
図3より，\( \ x_{\mathrm {1}} \ \)における電圧変化\( \ \mathit {\Delta } V \ \)は，
\[
\begin{eqnarray}
\mathit {\Delta } V&=&x_{\mathrm {1}}\cdot \mathit {\Delta } Q \\[ 5pt ] &=&x_{\mathrm {1}}\cdot \frac {x_{\mathrm {2}}}{x_{\mathrm {1}}+x_{\mathrm {2}}}\mathit {\Delta } q \\[ 5pt ] &=&\frac {x_{\mathrm {1}}x_{\mathrm {2}}}{x_{\mathrm {1}}+x_{\mathrm {2}}}\mathit {\Delta } q　・・・・・・・・・・　③ \\[ 5pt ] \end{eqnarray}
\] となる。題意より，変圧器のタップ調整を行わない\( \ \left( \mathit {\Delta } n =0 \right) \ \)ので，
\[
\begin{eqnarray}
\mathit {\Delta } V&=&A_{\mathrm {q}}\cdot \mathit {\Delta } q　・・・・・・・・・・・・　④ \\[ 5pt ] \end{eqnarray}
\] となるので，③及び④を係数比較すると，
\[
\begin{eqnarray}
A_{\mathrm {q}}&=&\frac {x_{\mathrm {1}}x_{\mathrm {2}}}{x_{\mathrm {1}}+x_{\mathrm {2}}} \\[ 5pt ] \end{eqnarray}
\] と求められる。