《電力・管理》〈送電〉[H25:問4]送電線の電力円線図に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

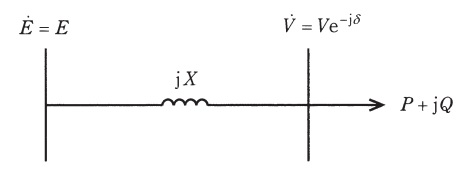
図に示すように電圧\( \ E \ \)の無限大母線から，リアクタンス\( \ X \ \)の送電線で負荷に電力を供給している。負荷の有効電力を\( \ P \ \)，無効電力を\( \ Q \ \)(遅れ無効電力を正とする。)，負荷端の複素電圧を\( \ V\mathrm {e}^{-\mathrm {j}\delta } \ \)として次の問に答えよ。

なお，\( \ X=0.2 \ \mathrm {[p.u.]} \ \)，\( \ E=1.0 \ \mathrm {[p.u.]} \ \)とし，送電線の抵抗と静電容量は無視できるものとする。また，負荷の\( \ P \ \)，\( \ Q \ \)は電圧に対し定電力特性をもつものとする。

(1)　負荷の\( \ P \ \)，\( \ Q \ \)を与えられた変数(\( \ E \ \)，\( \ V \ \)，\( \ X \ \)，\( \ \delta \ \))で示せ。

(2)　(1)で得られた式から\( \ \delta \ \)を消去し，\( \ P \ \)，\( \ Q \ \)と\( \ V \ \)の関係式，すなわち電力円線図を表す方程式を導け。

(3)　負荷の力率を\( \ 1.0 \ \)としたときの負荷端電圧\( \ V \ \)の値を求めることができる\( \ P \ \)の最大値，すなわち電圧安定性を維持できる限界点の\( \ P \ \)(電圧安定限界値)を与えられた数値を用いて求めよ。((2)で得られた式は\( \ V^{2} \ \)に関する二次方程式であることを利用せよ。)

(4)　(3)と同様に，負荷の力率を\( \ 0.9 \ \)(進み)としたときの\( \ P \ \)の最大値(電圧安定限界値)を求めよ。

(5)　負荷の力率を一定にして\( \ P \ \)を増加したとき，\( \ V=1.0 \ \mathrm {[p.u.]} \ \)で\( \ P \ \)が最大(電圧安定限界)となった。そのときの\( \ P \ \)の最大値(電圧安定限界値)を求めよ。

【ワンポイント解説】

考え方自体はそれほど難しい内容ではありませんが，(4)と(5)は計算が非常に複雑となり，一種並みの問題と言えると思います。試験まで期間がある場合はじっくり解いてみると良い勉強になると思います。

1.オイラーの公式
複素計算で用いるオイラーの公式は以下の通りとなります。
\[
\begin{eqnarray}
\mathrm {e}^{\mathrm {j}\theta }&=&\cos \theta +\mathrm {j}\sin \theta \\[ 5pt ] \mathrm {e}^{\mathrm {-j}\theta }&=&\cos \theta -\mathrm {j}\sin \theta \\[ 5pt ] \end{eqnarray}
\]

2.遅れ無効電力を正とした時の電力の導出式
遅れ無効電力を正とした時，電力\( \ P+\mathrm {j}Q \ \mathrm {[p.u.]} \ \)を負荷電圧\( \ \dot V \ \mathrm {[p.u.]} \ \)及び\( \ \dot I \ \mathrm {[p.u.]} \ \)で表すと，
\[
\begin{eqnarray}
P+\mathrm {j}Q&=&\dot V \overline {\dot I} \\[ 5pt ] \end{eqnarray}
\] となります。ちなみに進み無効電力を正とした時は，
\[
\begin{eqnarray}
P+\mathrm {j}Q&=&\overline {\dot V} \dot I \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)負荷の\( \ P \ \)，\( \ Q \ \)を与えられた変数(\( \ E \ \)，\( \ V \ \)，\( \ X \ \)，\( \ \delta \ \))で示す
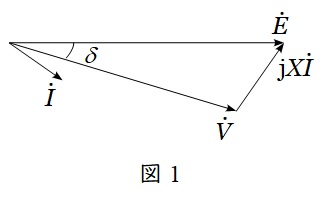
題意に沿ってベクトル図を描くと図1のようになる。図1より，
\[
\begin{eqnarray}
\dot E&=&\dot V+\mathrm {j}X\dot I \\[ 5pt ] \end{eqnarray}
\] であるから，
\[
\begin{eqnarray}
\dot I&=&\frac {\dot E-\dot V}{\mathrm {j}X} \\[ 5pt ] \end{eqnarray}
\] となる。ワンポイント解説「2.遅れ無効電力を正とした時の電力の導出式」より，
\[
\begin{eqnarray}
P+\mathrm {j}Q&=&\dot V \overline {\dot I} \\[ 5pt ] &=&\dot V \cdot {\frac {\overline {\dot E-\dot V}}{\overline {\mathrm {j}X}}} \\[ 5pt ] &=&V\mathrm {e}^{-\mathrm {j}\delta }\cdot \frac {E-V\mathrm {e}^{\mathrm {j}\delta }}{-\mathrm {j}X} \\[ 5pt ] &=&\mathrm {j}\cdot \frac {EV\mathrm {e}^{-\mathrm {j}\delta }-V^{2}}{X} \\[ 5pt ] &=&\mathrm {j}\cdot \frac {EV\left( \cos \delta -\mathrm {j}\sin \delta \right) -V^{2}}{X} \\[ 5pt ] &=&\frac {EV\sin \delta }{X}+\mathrm {j}\frac {EV\cos \delta -V^{2}}{X} \\[ 5pt ] \end{eqnarray}
\] となり，
\[
\begin{eqnarray}
P&=&\frac {EV\sin \delta }{X} \\[ 5pt ] Q&=&\frac {EV\cos \delta -V^{2}}{X} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)\( \ P \ \)，\( \ Q \ \)と\( \ V \ \)の関係式，すなわち電力円線図を表す方程式を導く
(1)解答式より，
\[
\begin{eqnarray}
\sin \delta &=&\frac {PX}{EV} \\[ 5pt ] \cos \delta &=&\frac {QX+V^{2}}{EV} \\[ 5pt ] \end{eqnarray}
\] であり，\( \ \sin ^{2}\delta +\cos ^{2}\delta =1 \ \)であるから，
\[
\begin{eqnarray}
\left( \frac {PX}{EV} \right) ^{2}+\left( \frac {QX+V^{2}}{EV}\right) ^{2}&=&1 \\[ 5pt ] P^{2}+\left( Q+\frac {V^{2}}{X}\right) ^{2}&=&\left( \frac {EV}{X}\right) ^{2} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)負荷の力率を\( \ 1.0 \ \)としたときの負荷端電圧\( \ V \ \)の値を求めることができる\( \ P \ \)の最大値
題意より，\( \ X=0.2 \ \mathrm {[p.u.]} \ \)，\( \ E=1.0 \ \mathrm {[p.u.]} \ \)，\( \ Q=0 \ \mathrm {[p.u.]} \ \)であるから，
\[
\begin{eqnarray}
P^{2}+\left( 0+\frac {V^{2}}{0.2}\right) ^{2}&=&\left( \frac {1\times V}{0.2}\right) ^{2} \\[ 5pt ] P^{2}+\frac {V^{4}}{0.04}&=&\frac {V^{2}}{0.04} \\[ 5pt ] 25V^{4}-25V^{2}+P^{2}&=&0 \\[ 5pt ] \end{eqnarray}
\] となる。電圧安定限界値は上式の判別式が零となる時であるから，
\[
\begin{eqnarray}
25^{2}-4\times 25 \times P^{2}&=&0 \\[ 5pt ] P^{2}&=&6.25 \\[ 5pt ] P&=&2.5 \ \mathrm {[p.u.]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)負荷の力率を\( \ 0.9 \ \)(進み)としたときの負荷端電圧\( \ V \ \)の値を求めることができる\( \ P \ \)の最大値
負荷の力率が\( \ 0.9 \ \)(進み)の時，\( \ Q \ \)を\( \ P \ \)を用いて表すと，
\[
\begin{eqnarray}
Q&=&-\frac {\sqrt {1-0.9^{2}}}{0.9}P \\[ 5pt ] &≒&-0.48432P \\[ 5pt ] \end{eqnarray}
\] となるので，(2)の解答式は，
\[
\begin{eqnarray}
P^{2}+\left( -0.48432P+\frac {V^{2}}{0.2}\right) ^{2}&=&\left( \frac {1\times V}{0.2}\right) ^{2} \\[ 5pt ] P^{2}+0.23457P^{2}-4.8432PV^{2}+25V^{4}&=&25V^{2} \\[ 5pt ] 25V^{4}-\left( 4.8432P+25\right) V^{2}+1.2346P^{2}&=&0 \\[ 5pt ] \end{eqnarray}
\] となる。電圧安定限界値は上式の判別式が零となる時であるから，
\[
\begin{eqnarray}
\left( 4.8432P+25\right) ^{2}-4\times 25 \times 1.2346P^{2}&=&0 \\[ 5pt ] 23.457P^{2}+242.16P+625-123.46P^{2}&=&0 \\[ 5pt ] 100P^{2}-242.16P-625&=&0 \\[ 5pt ] P^{2}-2.4216P-6.25&=&0 \\[ 5pt ] P&=&\frac {2.4216±\sqrt {2.4216^{2}+4\times 6.25}}{2} \\[ 5pt ] &≒&3.9886，-1.5670 \ \mathrm {[p.u.]} \\[ 5pt ] \end{eqnarray}
\] となり，\( \ P＞0 \ \)の条件より，\( \ P=3.99 \ \mathrm {[p.u.]} \ \)と求められる。

(5)\( \ V=1.0 \ \mathrm {[p.u.]} \ \)で\( \ P \ \)が最大(電圧安定限界)となったときの\( \ P \ \)の最大値
\( \ Q=-P\tan \theta \ \)であるから，(2)の解答式は，
\[
\begin{eqnarray}
P^{2}+\left( -P\tan \theta +\frac {V^{2}}{0.2}\right) ^{2}&=&\left( \frac {1\times V}{0.2}\right) ^{2} \\[ 5pt ] P^{2}+P^{2}\tan ^{2}\theta -10PV^{2}\tan \theta +25V^{4}&=&25V^{2} \\[ 5pt ] 25V^{4}-\left( 10P\tan \theta +25\right) V^{2}+P^{2}\left( 1+\tan ^{2}\theta \right) &=&0 \\[ 5pt ] V^{2}&=&\frac {10P\tan \theta +25±\sqrt {\left( 10P\tan \theta +25\right) ^{2}-4\times 25 \times P^{2}\left( 1+\tan ^{2}\theta \right) }}{2\times 25} \\[ 5pt ] &=&\frac {10P\tan \theta +25±\sqrt {\left( 10P\tan \theta +25\right) ^{2}-4\times 25 \times P^{2}\left( 1+\tan ^{2}\theta \right) }}{50}　・・・・・・・・・　① \\[ 5pt ] \end{eqnarray}
\] となる。\( \ P \ \)を最大すなわち安定限界にするには，①の根号内を零とすればよいので，
\[
\begin{eqnarray}
V^{2}&=&\frac {10P\tan \theta +25}{50} \\[ 5pt ] &=&0.2P\tan \theta +0.5 \\[ 5pt ] \end{eqnarray}
\] となる。この時，\( \ V=1.0 \ \mathrm {[p.u.]} \ \)であるから，
\[
\begin{eqnarray}
1&=&0.2P\tan \theta +0.5 \\[ 5pt ] P\tan \theta &=&2.5 \\[ 5pt ] \end{eqnarray}
\] となる。これを①の安定判別式に代入すると，
\[
\begin{eqnarray}
\left( 10P\tan \theta +25\right) ^{2}-4\times 25 \times P^{2}\left( 1+\tan ^{2}\theta \right) &=&0 \\[ 5pt ] \left( 10\times 2.5 +25\right) ^{2}-100 \left( P^{2}+2.5 ^{2}\right) &=&0 \\[ 5pt ] 2500-100 P^{2}-625 &=&0 \\[ 5pt ] P^{2}&=&18.75 \\[ 5pt ] P&≒&4.3301　→　4.33 \ \mathrm {[p.u.]} \\[ 5pt ] \end{eqnarray}
\] と求められる。