《電力・管理》〈配電〉[H25:問5]高調波電流の流出に関する計算・論説問題

【問題】

【難易度】★★☆☆☆（やや易しい）

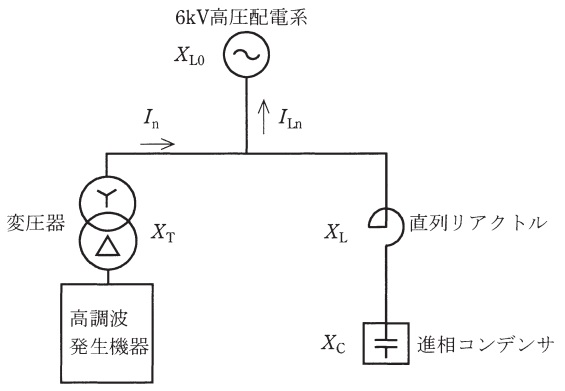
図のような三相$\ 3 \ $線式$\ 6 \ \mathrm {kV} \ $高圧配電系から受電している需要家がある。負荷の一部に三相の高調波発生機器があり，高調波電流$\ I_{\mathrm {n}} \ $を流出している。また，進相コンデンサにはそのリアクタンスの$\ 6 \ \mathrm {[％]} \ $のリアクタンスを有する直列リアクトルが接続されている。

ただし，基準容量により換算した各部のリアクタンスは，$\ X_{\mathrm {L0}}=0.20 \ \mathrm {[p.u.]} \ $，$\ X_{\mathrm {C}}=30.0 \ \mathrm {[p.u.]} \ $，$\ X_{\mathrm {T}}=0.05 \ \mathrm {[p.u.]} \ $とする。このとき，次の問に答えよ。

(1)　進相コンデンサに直列リアクトルを接続する理由を二つ述べよ。

(2)　流出している高調波電流を高圧配電系に換算した第$\ 5 \ $高調波電流$\ I_{5} \ $が$\ 10 \ \mathrm {[A]} \ $であったとき，高圧配電系に流出する電流$\ I_{\mathrm {Ln}} \ $のうち第$\ 5 \ $高調波電流$\ I_{\mathrm {L5}} \ \mathrm {[A]} \ $を求めよ。

(3)　$\ 6 \ \mathrm {[％]} \ $の直列リアクトルを接続しない場合の高圧配電系に流出する第$\ 5 \ $高調波電流を$\ {I_{\mathrm {L5}}}^{\prime } \ \mathrm {[A]} \ $とすると，$\ {I_{\mathrm {L5}}}^{\prime } \ $は，接続時の流出電流$\ I_{\mathrm {L5}} \ $の何$\ \mathrm {[％]} \ $となるか求めよ。

【ワンポイント解説】

高調波に関する問題です。過去にも類題が出題されたことがあるような問題となっています。計算量も少ないので，単位法アレルギーでなければ平成25年度の中では最も完答したい計算問題となると思います。

1.第$\ 5 \ $高調波に対するリアクタンス
リアクトルとコンデンサの基本波リアクタンス$\ X_{\mathrm {L}} \ $及び$\ X_{\mathrm {C}} \ $は，

$$\begin{eqnarray} \mathrm {j}X_{\mathrm {L}}&=&\mathrm {j}\omega L \\[ 5pt ] &=&\mathrm {j}2\pi f L \\[ 5pt ] -\mathrm {j}X_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C} \\[ 5pt ] &=&\frac {1}{\mathrm {j}2\pi f C} \\[ 5pt ] \end{eqnarray}$$ となりますが，第$\ 5 \ $高調波に対するリアクタンス$\ X_{\mathrm {L5}} \ $及び$\ X_{\mathrm {C5}} \ $は，
$$\begin{eqnarray} \mathrm {j}X_{\mathrm {L5}}&=&\mathrm {j}2\pi \cdot 5f L \\[ 5pt ] &=&\mathrm {j}10\pi f L \\[ 5pt ] -\mathrm {j}X_{\mathrm {C5}}&=&\frac {1}{\mathrm {j}2\pi \cdot 5f C} \\[ 5pt ] &=&\frac {1}{\mathrm {j}10\pi f C} \\[ 5pt ] \end{eqnarray}$$ となります。リアクトルは$\ 5 \ $倍，コンデンサは$\ \displaystyle \frac {1}{5} \ $倍となります。

【解答】

(1)進相コンデンサに直列リアクトルを接続する理由を二つ
(ポイント)
・ワンポイント解説「1.第$\ 5 \ $高調波に対するリアクタンス」の通り，リアクトルは基本波に対するリアクタンスが小さくても高調波に対しては大きな影響を与えることができます。一方コンデンサは，基本波に対するリアクタンスが大きくても，高調波になるとモロに影響が出てしまう可能性があります。したがって，それに関連するような内容を記載すれば良いと思います。

(試験センター解答例)
①　配電系に流出する高調波電流を抑制し，配電系の電圧ひずみ率の上昇を抑える。
②　含有率の多い低次の高調波電流（第$\ 5 \ $調波等）による，コンデンサの過負荷を抑制する。
③　進相コンデンサの投入時の突入電流を抑制する。
④　進相コンデンサの開放時に，再点弧を発生した場合，そのサージ電圧を抑制する。

(2)$\ I_{5} \ $が$\ 10 \ \mathrm {[A]} \ $であったとき，高圧配電系に流出する第$\ 5 \ $高調波電流$\ I_{\mathrm {L5}} \ \mathrm {[A]} \ $
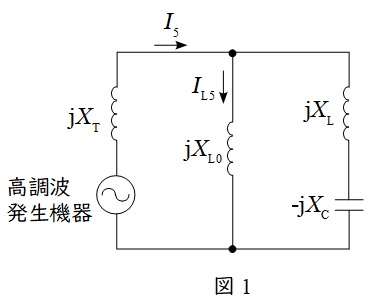
高調波電流に関する等価回路は図1のようになる。
それぞれのリアクトル及びコンデンサの第$\ 5 \ $高調波に対するリアクタンスは，ワンポイント解説「1.第$\ 5 \ $高調波に対するリアクタンス」の通り，

$$\begin{eqnarray} \mathrm {j}X_{\mathrm {L05}}&=&\mathrm {j}X_{\mathrm {L0}}\times 5 \\[ 5pt ] &=&\mathrm {j}0.20\times 5 \\[ 5pt ] &=&\mathrm {j}1.0 \ \mathrm {[p.u.]} \\[ 5pt ] -\mathrm {j}X_{\mathrm {C5}}&=&-\mathrm {j}X_{\mathrm {C}}\times \frac {1}{5} \\[ 5pt ] &=&-\mathrm {j}30.0\times \frac {1}{5} \\[ 5pt ] &=&-\mathrm {j}6.0 \ \mathrm {[p.u.]} \\[ 5pt ] \mathrm {j}X_{\mathrm {L5}}&=&\mathrm {j}X_{\mathrm {L}}\times 5 \\[ 5pt ] &=&\mathrm {j}X_{\mathrm {C}}\times 0.06\times 5 \\[ 5pt ] &=&\mathrm {j}30\times 0.06\times 5 \\[ 5pt ] &=&\mathrm {j}9.0 \ \mathrm {[p.u.]} \\[ 5pt ] \end{eqnarray}$$ となるので，分流の法則より，高圧配電系に流出する第$\ 5 \ $高調波電流$\ I_{\mathrm {L5}} \ \mathrm {[A]} \ $は，
$$\begin{eqnarray} I_{\mathrm {L5}}&=&\frac {\mathrm {j}X_{\mathrm {L5}}-\mathrm {j}X_{\mathrm {C5}}}{\mathrm {j}X_{\mathrm {L05}}+\mathrm {j}X_{\mathrm {L5}}-\mathrm {j}X_{\mathrm {C5}}}I_{5} \\[ 5pt ] &=&\frac {\mathrm {j}9.0-\mathrm {j}6.0}{\mathrm {j}1.0+\mathrm {j}9.0-\mathrm {j}6.0}\times 10 \\[ 5pt ] &=&\frac {3}{4}\times 10 \\[ 5pt ] &=&7.5 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}$$ と求められる。

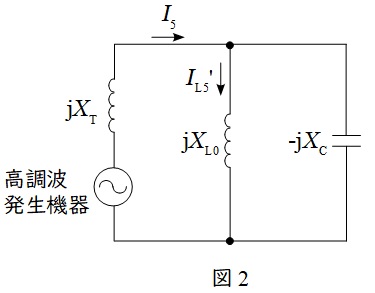
(3)直列リアクトルを接続しない場合の$\ 5 \ $高調波電流$\ {I_{\mathrm {L5}}}^{\prime } \ $は，$\ I_{\mathrm {L5}} \ $の何$\ \mathrm {[％]} \ $となるか
直列リアクトルを接続しない場合の等価回路は図2のようになる。分流の法則より，高圧配電系に流出する第$\ 5 \ $高調波電流$\ {I_{\mathrm {L5}}}^{\prime } \ \mathrm {[A]} \ $は，

$$\begin{eqnarray} {I_{\mathrm {L5}}}^{\prime }&=&\frac {-\mathrm {j}X_{\mathrm {C5}}}{\mathrm {j}X_{\mathrm {L05}}-\mathrm {j}X_{\mathrm {C5}}}I_{5} \\[ 5pt ] &=&\frac {-\mathrm {j}6.0}{\mathrm {j}1.0-\mathrm {j}6.0}\times 10 \\[ 5pt ] &=&\frac {6}{5}\times 10 \\[ 5pt ] &=&12 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}$$ となり，
$$\begin{eqnarray} \frac {{I_{\mathrm {L5}}}^{\prime }}{I_{\mathrm {L5}}}&=&\frac {12}{7.5} \\[ 5pt ] &=&1.6　→　160 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}$$ と求められる。