【問題】
【難易度】★★★★☆(やや難しい)
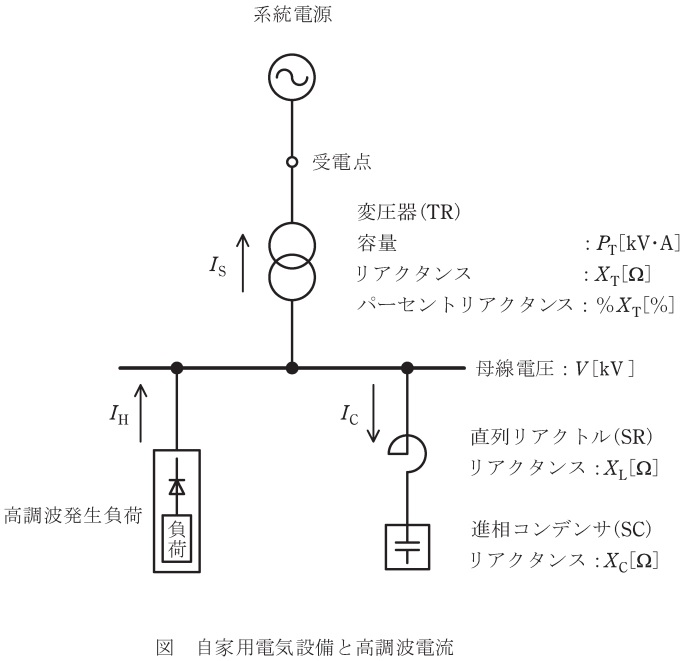
図は系統電源に接続された自家用電気設備の単線結線図である。変圧器の\(2\)次側母線には高調波を発生する負荷設備と力率改善用の直列リアクトル付進相コンデンサ設備が設置されている。\(X_{\mathrm {T}}\),\(X_{\mathrm {L}}\),\(X_{\mathrm {C}}\)は,それぞれ変圧器,直列リアクトル,進相コンデンサの基本波におけるリアクタンスの大きさ(\(\Omega \)値)である。また,電流\(I_{\mathrm {H}}\),\(I_{\mathrm {S}}\),\(I_{\mathrm {C}}\)は,それぞれ高調波発生負荷からの高調波電流,系統電源側に流出する高調波電流,進相コンデンサ設備に流入する高調波電流とする。このとき,次の問に答えよ。ただし,系統電源側のインピーダンス及び変圧器の抵抗分は無視するものとする。
(1)\( \ n \ \)次高調波電流源を電源とする高調波等価回路を描くとともに,\(I_{\mathrm {Hn}}\),\(I_{\mathrm {Sn}}\),\(I_{\mathrm {Cn}}\)それぞれに対し,電流の方向を矢印で示せ。ただし,\( \ n \ \)次高調波電流源の電流を\( \ I_{\mathrm {Hn}}\),系統電源側に流出する\( \ n \ \)次高調波電流を\( \ I_{\mathrm {Sn}}\),進相コンデンサ設備に流入する\( \ n \ \)次高調波電流を\( \ I_{\mathrm {Cn}} \ \)とする。
(2) (1)の\( \ n \ \)次高調波等価回路において,\( \ n \ \)次高調波電流源の電流\( \ I_{\mathrm {Hn}} \ \)と各部のリアクタンスの大きさを用いて,進相コンデンサ設備に流入する\( \ n \ \)次高調波電流\( \ I_{\mathrm {Cn}} \ \)を表す式を示せ。
(3)\( \ I_{\mathrm {Cn}} \ \)を表す式において,回路で共振を起こす条件式を示せ。
(4)\( \ I_{\mathrm {Cn}} \ \)を表す式において,進相コンデンサ設備に流入する\( \ n \ \)次高調波電流が,高調波発生源の電流よりも大きくならないようにするための条件式を示せ。
\( \ n=5 \ \)(第\(5\)高調波)の場合,直列リアクトルのリアクタンスの大きさは進相コンデンサのリアクタンスの大きさの何\([%]\)以上であることが必要か示せ。
(5)\( \ 6% \ \)直列リアクトル付進相コンデンサ設備の場合,高調波発生源に第\(3\)高調波が多く含まれている場合,進相コンデンサの容量によっては共振状態となり,第\(3\)高調波電流が異常に増大する場合がある。このとき,進相コンデンサのリアクタンスの大きさ\( \ X_{\mathrm {C}} \ \mathrm {[\Omega ]} \ \)と変圧器のリアクタンスの大きさ\( \ X_{\mathrm {T}} \ \mathrm {[\Omega ]} \ \)の関係式を示せ。また,進相コンデンサ容量は変圧器容量の何\([%]\)か示せ。変圧器の容量を\( \ P_{\mathrm {T}} \ \mathrm {[kV\cdot A]}\),変圧器のパーセントリアクタンス\( \ %X_{\mathrm {T}} \ \)を\( \ 7.5% \ \)(自己容量基準),進相コンデンサ容量を\( \ Q_{\mathrm {C}} \ \mathrm {[kvar]}\)として計算せよ。
【ワンポイント解説】
一番のポイントはリアクトルのリアクタンスが周波数に比例し,コンデンサのリアクタンスが周波数に反比例することですが,本問の場合はそれだけでは完答までたどり着きません。判断が難しいところですが,時間配分のことを考慮すると途中まで解いて,別の問題が終わって時間が余れば残りを解くというような選択も視野に入れた方が良いと思います。
1.高調波でのリアクタンス
ある回路に電源周波数\(f\)の電源及びインダクタンス\(L\)のコイル,静電容量\(C\)のコンデンサが取り付けられている時,それぞれの基本波のリアクタンス\(X_{\mathrm {L}}\),\(X_{\mathrm {C}}\)は,
\[
\begin{eqnarray}
\mathrm {j}X_{\mathrm {L}}&=&\mathrm {j}\omega L \\[ 5pt ]
&=&\mathrm {j}2\pi f L \\[ 5pt ]
-\mathrm {j}X_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C} \\[ 5pt ]
&=&\frac {1}{\mathrm {j}2\pi f C} \\[ 5pt ]
\end{eqnarray}
\]
となります。この時,\(n\)次高調波に対するリアクタンス\(X_{\mathrm {nL}}\),\(X_{\mathrm {nC}}\)は,\(n\)倍の周波数となったと考えれば良いから,
\[
\begin{eqnarray}
\mathrm {j}X_{\mathrm {nL}}&=&\mathrm {j}\omega _{\mathrm {n}} L \\[ 5pt ]
&=&\mathrm {j}2\pi nf L \\[ 5pt ]
-\mathrm {j}X_{\mathrm {nC}}&=&\frac {1}{\mathrm {j}\omega _{\mathrm {n}} C} \\[ 5pt ]
&=&\frac {1}{\mathrm {j}2\pi nf C} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.百分率インピーダンス
基準容量を\(P_{\mathrm {B}}\),基準電圧を\(V_{\mathrm {B}}\)とすると,
\[
\begin{eqnarray}
%P&=&\frac {P \ \mathrm {[W]}}{P_{\mathrm {B}}}\times 100 \\[ 5pt ]
%V&=&\frac {V \ \mathrm {[V]}}{V_{\mathrm {B}}}\times 100 \\[ 5pt ]
%I&=&\frac {I \ \mathrm {[A]}}{I_{\mathrm {B}}}\times 100 \\[ 5pt ]
&=&\frac {I \ \mathrm {[A]}}{\displaystyle \frac {P_{\mathrm {B}}}{\sqrt {3}V_{\mathrm {B}}}}\times 100 \\[ 5pt ]
&=&\frac {\sqrt {3}V_{\mathrm {B}}}{P_{\mathrm {B}}}\cdot I \ \mathrm {[A]}\times 100 \\[ 5pt ]
%Z&=&\frac {Z \ \mathrm {[\Omega ]}}{Z_{\mathrm {B}}}\times 100 \\[ 5pt ]
&=&\frac {Z \ \mathrm {[\Omega ]}}{\displaystyle \frac {V_{\mathrm {B}}}{\sqrt {3}I_{\mathrm {B}}}}\times 100 \\[ 5pt ]
&=&\frac {\sqrt {3}}{V_{\mathrm {B}}}I_{\mathrm {B}}\cdot Z \ \mathrm {[\Omega ]}\times 100 \\[ 5pt ]
&=&\frac {\sqrt {3}}{V_{\mathrm {B}}} \frac {P_{\mathrm {B}}}{\sqrt {3}V_{\mathrm {B}}}\cdot Z \ \mathrm {[\Omega ]}\times 100 \\[ 5pt ]
&=&\frac {P_{\mathrm {B}}}{V_{\mathrm {B}}^{2}}\cdot Z \ \mathrm {[\Omega ]}\times 100 \\[ 5pt ]
\end{eqnarray}
\]
となります。最後の\(%Z\)の式は公式として暗記しておきましょう。
【解答】
(1)\( \ n \ \)次高調波電流源を電源とする高調波等価回路を描くとともに,\(I_{\mathrm {Hn}}\),\(I_{\mathrm {Sn}}\),\(I_{\mathrm {Cn}}\)それぞれに対し,電流の方向を矢印で示す
等価回路において,系統電源は電圧源とみなし短絡すれば良い。また,ワンポイント解説「1.高調波でのリアクタンス」より,変圧器と直列リアクトルのリアクタンスは\(n\)倍,進相コンデンサのリアクタンスは\(\displaystyle \frac {1}{n}\)倍すれば良いから,等価回路を図1のようになる。
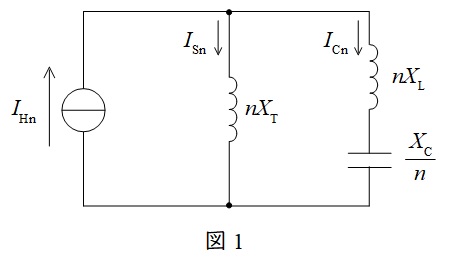
(2)進相コンデンサ設備に流入する\( \ n \ \)次高調波電流\( \ I_{\mathrm {Cn}} \ \)を表す式
図1において,分流の法則より,
\[
\begin{eqnarray}
I_{\mathrm {Cn}}&=&\frac {\mathrm {j}nX_{\mathrm{T}}}{\mathrm {j}nX_{\mathrm{T}}+\mathrm {j}\left( nX_{\mathrm{L}}-\displaystyle \frac {X_{\mathrm{C}}}{n}\right) }\cdot I_{\mathrm {Hn}} \\[ 5pt ]
&=&\frac {nX_{\mathrm{T}}}{nX_{\mathrm{T}}+\left( nX_{\mathrm{L}}-\displaystyle \frac {X_{\mathrm{C}}}{n}\right) }\cdot I_{\mathrm {Hn}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)回路で共振を起こす条件式
(2)の式において,共振を起こし,電流が異常に上昇するのは分母が零の時であるので,
\[
\begin{eqnarray}
nX_{\mathrm{T}}+\left( nX_{\mathrm{L}}-\displaystyle \frac {X_{\mathrm{C}}}{n}\right) &=&0 \\[ 5pt ]
\end{eqnarray}
\]
となる。
(4)進相コンデンサ設備に流入する\( \ n \ \)次高調波電流が,高調波発生源の電流よりも大きくならないようにするための条件式と\( \ n=5 \ \)(第\(5\)高調波)の時直列リアクトルのリアクタンスの大きさ
条件を満たすのは\(I_{\mathrm {Cn}}≦I_{\mathrm {Hn}}\)の時であるから,(2)の解答式より,
\[
\begin{eqnarray}
\frac {nX_{\mathrm{T}}}{nX_{\mathrm{T}}+\left( nX_{\mathrm{L}}-\displaystyle \frac {X_{\mathrm{C}}}{n}\right) }\cdot I_{\mathrm {Hn}}&≦&I_{\mathrm {Hn}} \\[ 5pt ]
\frac {nX_{\mathrm{T}}}{nX_{\mathrm{T}}+\left( nX_{\mathrm{L}}-\displaystyle \frac {X_{\mathrm{C}}}{n}\right) }&≦&1 \\[ 5pt ]
nX_{\mathrm{T}}&≦&nX_{\mathrm{T}}+\left( nX_{\mathrm{L}}-\displaystyle \frac {X_{\mathrm{C}}}{n}\right) \\[ 5pt ]
nX_{\mathrm{L}}-\displaystyle \frac {X_{\mathrm{C}}}{n}&≧&0 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
\(n=5\)の時,
\[
\begin{eqnarray}
5X_{\mathrm{L}}-\frac {X_{\mathrm{C}}}{5}&≧&0 \\[ 5pt ]
5X_{\mathrm{L}}&≧&\frac {X_{\mathrm{C}}}{5} \\[ 5pt ]
X_{\mathrm{L}}&≧&\frac {X_{\mathrm{C}}}{25} \\[ 5pt ]
X_{\mathrm{L}}&≧&0.04X_{\mathrm{C}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,直列リアクトルのリアクタンスの大きさは進相コンデンサのリアクタンスの大きさの4\(%\)以上であることが必要となる。
(5)進相コンデンサのリアクタンスの大きさ\( \ X_{\mathrm {C}} \ \mathrm {[\Omega ]} \ \)と変圧器のリアクタンスの大きさ\( \ X_{\mathrm {T}} \ \mathrm {[\Omega ]} \ \)の関係式と進相コンデンサ容量は変圧器容量の何\([%]\)か
題意より,\(X_{\mathrm {L}}=0.06X_{\mathrm {C}}\)であり,第3高調波電流をそれぞれ,\(I_{\mathrm {H3}}\),\(I_{\mathrm {S3}}\),\(I_{\mathrm {C3}}\)とすると,(2)の解答式に\(n=3\)を代入すれば良いから,
\[
\begin{eqnarray}
I_{\mathrm {C3}}&=&\frac {3X_{\mathrm{T}}}{3X_{\mathrm{T}}+\left( 3X_{\mathrm{L}}-\displaystyle \frac {X_{\mathrm{C}}}{3}\right) }\cdot I_{\mathrm {H3}} \\[ 5pt ]
&=&\frac {3X_{\mathrm{T}}}{3X_{\mathrm{T}}+\left( 3\times 0.06X_{\mathrm {C}}-\displaystyle \frac {X_{\mathrm{C}}}{3}\right) }\cdot I_{\mathrm {H3}} \\[ 5pt ]
&=&\frac {3X_{\mathrm{T}}}{3X_{\mathrm{T}}-\displaystyle \frac {0.46}{3}X_{\mathrm {C}}}\cdot I_{\mathrm {H3}} \\[ 5pt ]
\end{eqnarray}
\]
となる。共振状態になるのは分母が零の時であるから,
\[
\begin{eqnarray}
3X_{\mathrm{T}}-\frac {0.46}{3}X_{\mathrm {C}}&=&0 \\[ 5pt ]
3X_{\mathrm{T}}&=&\frac {0.46}{3}X_{\mathrm {C}} \\[ 5pt ]
X_{\mathrm {C}}&=&\frac {9}{0.46}X_{\mathrm{T}} \\[ 5pt ]
&≒&19.565X_{\mathrm{T}} → 19.6X_{\mathrm{T}} ・・・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
の時となる。
ワンポイント解説「2.百分率インピーダンス」より,変圧器容量\( \ P_{\mathrm {T}} \ \mathrm {[kV\cdot A]}\),変圧器のパーセントリアクタンス\( \ %X_{\mathrm {T}} \ \)には,
\[
\begin{eqnarray}
%X_{\mathrm {T}}&=&\frac {P_{\mathrm {T}}\times 10^{3}}{\left( V\times 10^{3}\right) ^{2}}\cdot X_{\mathrm {T}}\times 100 \\[ 5pt ]
\end{eqnarray}
\]
の関係が成立するから,上式を整理すると,
\[
\begin{eqnarray}
%X_{\mathrm {T}}&=&\frac {P_{\mathrm {T}}X_{\mathrm {T}}}{10V^{2}} \\[ 5pt ]
7.5&=&\frac {P_{\mathrm {T}}X_{\mathrm {T}}}{10V^{2}} \\[ 5pt ]
X_{\mathrm {T}}&=&\frac {75V^{2}}{P_{\mathrm {T}}} ・・・・・・・・・・・ ② \\[ 5pt ]
\end{eqnarray}
\]
となる。一方,進相コンデンサについて,進相コンデンサの分担電圧\(V_{\mathrm {C}}\)とすると,
\[
\begin{eqnarray}
\frac {V_{\mathrm {C}}}{-\mathrm {j}X_{\mathrm {C}}}&=&\frac {V}{\mathrm {j}\left( X_{\mathrm {L}}-X_{\mathrm {C}}\right) } \\[ 5pt ]
V_{\mathrm {C}}&=&\frac {X_{\mathrm {C}}}{X_{\mathrm {C}}-X_{\mathrm {L}}}V \\[ 5pt ]
&=&\frac {X_{\mathrm {C}}}{X_{\mathrm {C}}-0.06X_{\mathrm {C}}}V \\[ 5pt ]
&=&\frac {V}{0.94} \\[ 5pt ]
\end{eqnarray}
\]
であるから,進相コンデンサの容量\(Q_{\mathrm {C}}\)を求めると,
\[
\begin{eqnarray}
Q_{\mathrm {C}}\times 10^{3}&=&\sqrt {3}\left( V_{\mathrm {C}}\times 10^{3}\right) \times I_{\mathrm {C}} \\[ 5pt ]
&=&\sqrt {3}V_{\mathrm {C}}\times 10^{3} \cdot \frac {\displaystyle \frac {V_{\mathrm {C}}\times 10^{3}}{\sqrt{3}}}{X_{\mathrm {C}}} \\[ 5pt ]
&=&\frac {V_{\mathrm {C}}^{2}\times 10^{6}}{X_{\mathrm {C}}} \\[ 5pt ]
Q_{\mathrm {C}}&=&\frac {V_{\mathrm {C}}^{2}\times 10^{3}}{X_{\mathrm {C}}} \\[ 5pt ]
&=&\frac {V^{2}\times 10^{3}}{0.94^{2}\times X_{\mathrm {C}}} \\[ 5pt ]
\end{eqnarray}
\]
となる。①,②を代入すると,
\[
\begin{eqnarray}
Q_{\mathrm {C}}&=&\frac {V^{2}\times 10^{3}}{0.94^{2}\times X_{\mathrm {C}}} \\[ 5pt ]
&=&\frac {V^{2}\times 10^{3}}{0.94^{2}\times 19.565X_{\mathrm{T}}} \\[ 5pt ]
&=&\frac {V^{2}\times 10^{3}}{0.94^{2}\times 19.565\times \displaystyle \frac {75V^{2}}{P_{\mathrm {T}}}} \\[ 5pt ]
&=&\frac {10^{3}}{0.94^{2}\times 19.565\times 75}\cdot P_{\mathrm {T}} \\[ 5pt ]
\frac {Q_{\mathrm {C}}}{P_{\mathrm {T}}}&=&0.77126 → 77.1 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
※ 本解答では\(\displaystyle V_{\mathrm {C}}=\frac {V}{0.94}\)として計算しましたが,\(V_{\mathrm {C}}=V\)のままでも正解のようです。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは