《電力・管理》〈配電〉[R03:問4]三相３線式高圧配電線への分散形電源の系統連系に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

分散形電源の系統連系に関して，次の問に答えよ。

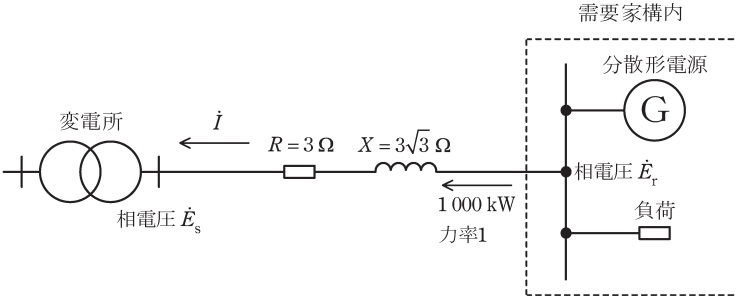
図に示す\( \ 6.6 \ \mathrm {kV} \ \)三相\( \ 3 \ \)線式高圧配電線の末端に，分散形電源を有する需要家が連系されている。

(1)　需要家から配電線へ逆潮流（力率\( \ 1 \ \)）がある場合の，需要家端の相電圧（\( \ 1 \ \)線と中性点間の電圧）\( \ {\dot E}_{\mathrm {r}} \ \)と変電所の相電圧\( \ {\dot E}_{\mathrm {s}} \ \)の関係を示すベクトル図及び関係式を\( \ {\dot E}_{\mathrm {s}} \ \)，\( \ {\dot E}_{\mathrm {r}} \ \)，\( \ \dot I \ \)，\( \ R \ \)，\( \ X \ \)を用いて描け。ただし，ベクトル図は\( \ {\dot E}_{\mathrm {r}} \ \)（位相\( \ 0 \ \)）を基準とし，電流\( \ \dot I \ \)は図中の矢印の向きを正とする。

(2)　小問(1)のベクトル図から需要家端の線間電圧値を求めよ。ただし，需要家端からの逆潮流は\( \ 1 \ 000 \ \mathrm {kW} \ \)，力率は\( \ 1 \ \)（分散形電源，負荷設備ともに\( \ 1 \ \)）であり，高圧配電線は当該需要家のみの専用線とし，\( \ 1 \ \)線当たりの抵抗\( \ R \ \)及びリアクタンス\( \ X \ \)はそれぞれ\( \ 3 \ \mathrm {\Omega } \ \)及び\( \ 3\sqrt {3} \ \mathrm {\Omega } \ \)，変電所端の線間電圧は\( \ 6.6 \ \mathrm {kV} \ \)で一定とする。

【ワンポイント解説】

分散形電源の系統連系に関する問題です。
逆潮流であることが受験生を悩ますところと，(2)の計算が多いので，令和\( \ 3 \ \)年度の計算問題の中では最も難易度が高い問題となります。
考え方自体は難しい問題ではないので，まずは考え方を理解するようにしましょう。

1.送配電線の電圧降下
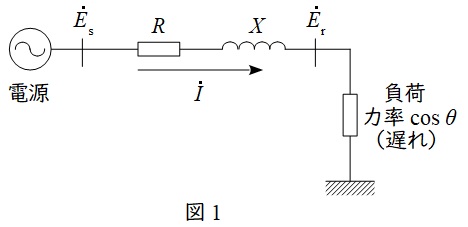
図1のような一般的な三相\( \ 3 \ \)線式送配電線路において，送電線には抵抗\( \ R \ \mathrm {[\Omega ]} \ \)及びリアクタンス\( \ X \ \mathrm {[\Omega ]} \ \)があるため，送電線での抵抗降下やリアクタンス降下が発生します。
送電端電圧（相電圧）を\( \ {\dot E}_{\mathrm {s}} \ \mathrm {[V]} \ \)，受電端に力率\( \ \cos \theta \ \)の負荷を接続したときの受電端電圧（相電圧）を\( \ {\dot E}_{\mathrm {r}} \ \mathrm {[V]} \ \)，送電線に流れる電流を\( \ \dot I \ \mathrm {[A]} \ \)とすると，
\[
\begin{eqnarray}
{\dot E}_{\mathrm {s}} &=&{\dot E}_{\mathrm {r}}+\left( R+\mathrm {j}X \right) \dot I \\[ 5pt ] \end{eqnarray}
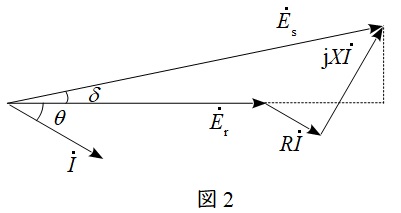
\] の関係があるため，ベクトル図で表すと図2のようになります。

2.二次方程式の解の公式
\( \ x \ \)に関する二次方程式\( \ ax^{2}+bx+c=0 \ \)の解は，
\[
\begin{eqnarray}
x &=&\frac {-b±\sqrt {b^{2}-4ac}}{2a} \\[ 5pt ] \end{eqnarray}
\] となりますが，仮に\( \ b=2B \ \)と表すことができる場合には，二次方程式\( \ ax^{2}+2Bx+c=0 \ \)の解は，
\[
\begin{eqnarray}
x &=&\frac {-B±\sqrt {B^{2}-ac}}{a} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)需要家端の相電圧\( \ {\dot E}_{\mathrm {r}} \ \)と変電所の相電圧\( \ {\dot E}_{\mathrm {s}} \ \)の関係を示すベクトル図及び関係式
題意より本問においては需要家から配電線への逆潮流が発生しているので，ワンポイント解説「1.送配電線の電圧降下」の関係式の\( \ {\dot E}_{\mathrm {s}} \ \mathrm {[V]} \ \)と\( \ {\dot E}_{\mathrm {r}} \ \mathrm {[V]} \ \)を入れ替えたものであるから，
\[
\begin{eqnarray}
{\dot E}_{\mathrm {r}} &=&{\dot E}_{\mathrm {s}}+\left( R+\mathrm {j}X \right) \dot I \\[ 5pt ] \end{eqnarray}
\] の関係が成立する。力率が\( \ 1 \ \)であることに注意してベクトル図で示すと図3のように求められる。

(2)需要家端の線間電圧値
図3のベクトル図において，三平方の定理を適用すると，
\[
\begin{eqnarray}
\left( E_{\mathrm {r}}-RI\right) ^{2}+\left( XI \right) ^{2} &=&E_{\mathrm {s}}^{2} \\[ 5pt ] \end{eqnarray}
\] となる。ここで，逆潮流\( \ P=3E_{\mathrm {r}}I \ \)すなわち\( \ \displaystyle I=\frac {P}{3E_{\mathrm {r}}} \ \)であるから，
\[
\begin{eqnarray}
\left( E_{\mathrm {r}}-RI\right) ^{2}+\left( XI \right) ^{2} &=&E_{\mathrm {s}}^{2} \\[ 5pt ] \left( E_{\mathrm {r}}-\frac {RP}{3E_{\mathrm {r}}}\right) ^{2}+\left( \frac {XP}{3E_{\mathrm {r}}} \right) ^{2} &=&E_{\mathrm {s}}^{2} \\[ 5pt ] \left( 3E_{\mathrm {r}}^{2}-RP\right) ^{2}+\left( XP \right) ^{2} &=&9E_{\mathrm {s}}^{2}E_{\mathrm {r}}^{2} \\[ 5pt ] 9E_{\mathrm {r}}^{4}-6RPE_{\mathrm {r}}^{2}+R^{2}P^{2}+X^{2}P^{2} &=&9E_{\mathrm {s}}^{2}E_{\mathrm {r}}^{2} \\[ 5pt ] 9E_{\mathrm {r}}^{4}-\left( 9E_{\mathrm {s}}^{2}+6RP\right) E_{\mathrm {r}}^{2}+\left( R^{2}+X^{2}\right) P^{2} &=&0 \\[ 5pt ] \end{eqnarray}
\] と整理できる。各値を代入すると，
\[
\begin{eqnarray}
9E_{\mathrm {r}}^{4}-\left\{ 9\left( \frac {6600}{\sqrt {3}}\right) ^{2}+6\times 3\times 1000\times 10^{3}\right\} E_{\mathrm {r}}^{2}+\left\{ 3^{2}+\left( 3\sqrt {3}\right) ^{2}\right\} \left( 1.0\times 10^{6}\right) ^{2} &=&0 \\[ 5pt ] 9E_{\mathrm {r}}^{4}-\left( 1.4868\times 10^{8}\right) E_{\mathrm {r}}^{2}+36\times 10^{12} &=&0 \\[ 5pt ] E_{\mathrm {r}}^{4}-\left( 1.6520\times 10^{7}\right) E_{\mathrm {r}}^{2}+4\times 10^{12} &=&0 \\[ 5pt ] E_{\mathrm {r}}^{4}-2\left( 8.260\times 10^{6}\right) E_{\mathrm {r}}^{2}+4\times 10^{12} &=&0 \\[ 5pt ] \end{eqnarray}
\] となるので，\( \ E_{\mathrm {r}}＞0 \ \)に注意して\( \ E_{\mathrm {r}}^{2} \ \)について解の公式を適用すると，
\[
\begin{eqnarray}
E_{\mathrm {r}}^{2} &=&8.260\times 10^{6}±\sqrt {\left( 8.260\times 10^{6}\right) ^{2}-4\times 10^{12}} \\[ 5pt ] &≒&8.260\times 10^{6}±8.0142\times 10^{6} \\[ 5pt ] &≒&16.274\times 10^{6}，0.2458\times 10^{6} \\[ 5pt ] E_{\mathrm {r}}&≒&4.0341\times 10^{3}，0.496\times 10^{3} \\[ 5pt ] &=&4.0341 \ \mathrm {[kV]}，\color {red} {0.496 \ \mathrm {[kV]}（不適）} \\[ 5pt ] \end{eqnarray}
\] となるので，需要家端の線間電圧の大きさ\( \ V_{\mathrm {r}} \ \mathrm {[kV]} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {r}} &=&\sqrt {3}E_{\mathrm {r}} \\[ 5pt ] &=&\sqrt {3}\times 4.0341 \\[ 5pt ] &≒&6.99 \ \mathrm {[kV]} \\[ 5pt ] \end{eqnarray}
\] と求められる。