《電力・管理》〈水力〉[R04:問1]調整池式の水力発電所の運用に関する計算問題

【問題】

【難易度】★☆☆☆☆（易しい）

調整池式の水力発電所の運用に関して，次の問に答えよ。

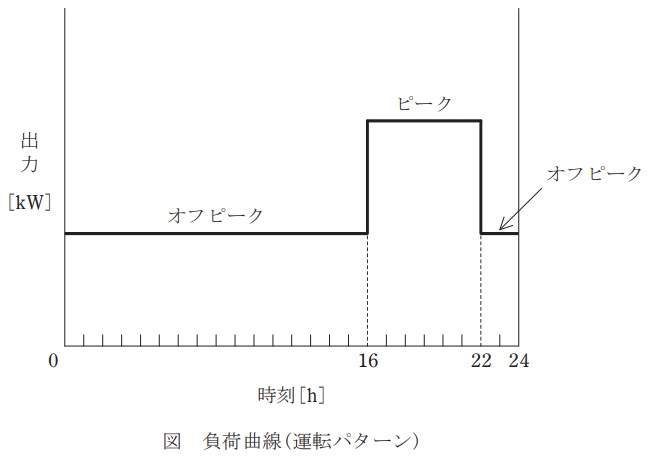
有効貯水量\( \ 180\times 10^{3} \ \mathrm {m^{3}} \ \)の調整池を有する有効落差\( \ 60 \ \mathrm {m} \ \)の水力発電所がある。自然流量が\( \ 20 \ \mathrm {m^{3} / s} \ \)であるとき，図に示す負荷曲線で運転した場合のピーク負荷時の出力\( \ \mathrm {[kW]} \ \)及びオフピーク負荷時の出力\( \ \mathrm {[kW]} \ \)を求めよ。ただし，年間を通して毎日同様の運転を繰り返すものとし，調整池は最大限活用し，オフピーク負荷時には越流させないこととする。

なお，水車と発電機の合成効率は，ピーク負荷時出力で\( \ 85 \ \mathrm {％} \ \)，オフピーク負荷時出力で\( \ 80 \ \mathrm {％} \ \)とする。

また，発電機の定格出力はピーク負荷を十分供給できるものとする。

【ワンポイント解説】

調整池式水力発電所の運用に関する問題です。
比較的取り組みやすい問題なので，ほとんどの受験生が選択したと予想されます。計算ミスに注意して完答を目指して下さい。
一次試験になりますが，平成24年電力科目問5に類題が出題されていますので，合わせて見ておくようにして下さい。

1.水力発電所の出力\( \ P \ \mathrm {[kW]} \ \)
水力発電所の使用水量を\( \ Q \ \left[ \mathrm {m^{3}／s} \right] \)，有効落差を\( \ H \ \left[ \mathrm {m} \right] \ \)，水車効率を\( \ \eta _{\mathrm {w}}\)，発電機効率を\( \ \eta _{\mathrm {g}} \ \)とすると，水力発電所の出力\( \ P \ \mathrm {[kW]} \ \)は，
\[
\begin{eqnarray}
P&=&9.8QH\eta _{\mathrm {w}} \eta _{\mathrm {g}} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

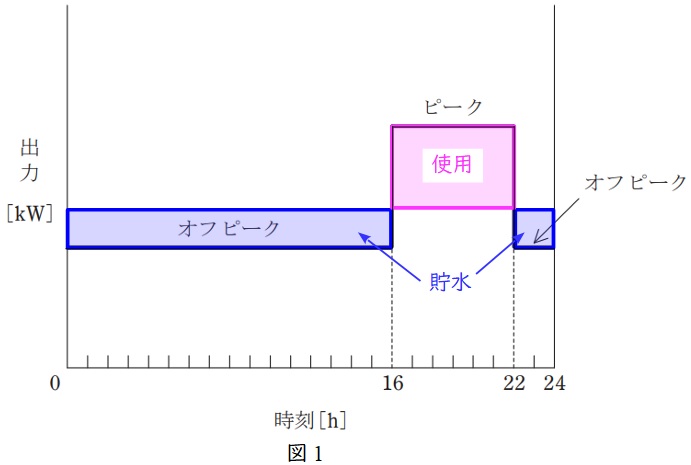
ピーク負荷時の使用水量を\( \ Q_{\mathrm {p}} \ \mathrm {[m^{3}]} \ \)，オフピーク負荷時の使用水量を\( \ Q_{\mathrm {o}} \ \mathrm {[m^{3}]} \ \)とすると，調整池は最大限活用するため，図1の通りピーク時に貯水池から使用される水量とオフピーク時に貯水される水量がともに有効貯水量\( \ 180\times 10^{3} \ \mathrm {m^{3}} \ \)であり，自然流量が\( \ 20 \ \mathrm {m^{3} / s} \ \)であるから，
\[
\begin{eqnarray}
\left( Q_{\mathrm {p}}-20\right) \times 3600\times 6&=&180\times 10^{3} \\[ 5pt ] Q_{\mathrm {p}}-20&≒&8.3333 \\[ 5pt ] Q_{\mathrm {p}}&≒&28.333 \ \mathrm {[m^{3}]} \\[ 5pt ] \left( 20-Q_{\mathrm {o}}\right) \times 3600\times 18&=&180\times 10^{3} \\[ 5pt ] 20-Q_{\mathrm {o}}&≒&2.7778 \\[ 5pt ] Q_{\mathrm {o}}&≒&17.222 \ \mathrm {[m^{3}]} \\[ 5pt ] \end{eqnarray}
\] となるので，ピーク負荷時の出力\( \ P_{\mathrm {p}} \ \mathrm {[kW]} \ \)及びオフピーク負荷時の出力\( \ P_{\mathrm {o}} \ \mathrm {[kW]} \ \)は，ワンポイント解説「1.水力発電所の出力\( \ P \ \mathrm {[kW]} \ \)」の通り，
\[
\begin{eqnarray}
P_{\mathrm {p}}&=&9.8Q_{\mathrm {p}}H\eta _{\mathrm {p}} \\[ 5pt ] &=&9.8\times 28.333\times 60\times 0.85 \\[ 5pt ] &≒&14 \ 200 \ \mathrm {[kW]} \\[ 5pt ] P_{\mathrm {o}}&=&9.8Q_{\mathrm {o}}H\eta _{\mathrm {o}} \\[ 5pt ] &=&9.8\times 17.222\times 60\times 0.80 \\[ 5pt ] &≒&8 \ 100 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。