【問題】
【難易度】★★★☆☆(普通)
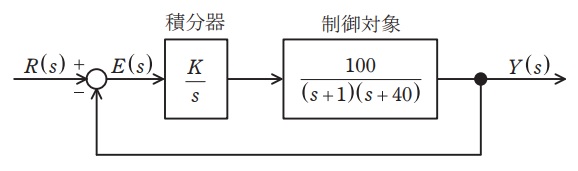
図に示すフィードバック制御系について,次の問に答えよ。ただし,\( \ R \left( s \right) \ \)は目標値,\( \ Y \left( s \right) \ \)は制御量,\( \ E \left( s \right) \ \)は制御偏差であり,時間信号\( \ r \left( t \right) \ \),\( \ y \left( t \right) \ \),\( \ e \left( t \right) \ \)をそれぞれラプラス変換したものである。
(1) フィードバック制御系の特性方程式を求めよ。
(2) フィードバック制御系を安定とする\( \ K \ \)の条件を求めよ。
(3) 目標値\( \ R \left( s \right) \ \)から制御偏差\( \ E \left( s \right) \ \)までの伝達関数\( \ T_{\mathrm {ER}} \left( s \right) \ \)を求めよ。
(4) \( \ K=2 \ \)とおく。目標値\( \ r \left( t \right) \ \)を傾き\( \ 2 \ \)でランプ変化させたときの定常速度偏差\( \ e_{\mathrm {v}} \ \)を求めよ。
(5) \( \ K=2 \ \)とおく。正弦関数\( \ 2\sin t \ \)で表される目標値\( \ r \left( t \right) \ \)に対し,定常状態での制御偏差\( \ e \left( t \right) \ \)は\( \ B \sin \left( t+\theta \right) \ \)で表される正弦関数となった。\( \ B \ \)の値を求めよ。
【ワンポイント解説】
フィードバック制御系の伝達関数から定常状態を検討する計算問題です。
考え方はそれほど難しくはありませんが,計算量が非常に多く\( \ 30 \ \)分で完答するには少し時間が足りない問題であった印象です。
(4)までは過去問でも頻出の内容となっていますので,部分点狙い(合格点狙い)としては選択しても良い問題かと思います。
1.基本的なラプラス変換
\( \ f(t) \ \)のラプラス変換を\( \ F(s) \ \)とすると以下のような関係があります。
\[
\begin{array}{|c|c|}
\hline
f(t) & F(s) \\
\hline
u (t) & \displaystyle \frac {1}{s} \\[ 5pt ]
K & \displaystyle \frac {K}{s} \\[ 5pt ]
t & \displaystyle \frac {1}{s^{2}} \\[ 5pt ]
\mathrm {e}^{at} & \displaystyle \frac {1}{s-a} \\[ 5pt ]
\sin \omega t & \displaystyle \frac {\omega }{s^{2}+\omega ^{2}} \\[ 5pt ]
\cos \omega t & \displaystyle \frac {s}{s^{2}+\omega ^{2}} \\[ 5pt ]
\hline
\end{array}
\]
2.ラウスの安定判別法
特性方程式\( \ a_{0}s^{n}+a_{1}s^{n-1}+a_{2}s^{n-2}+\cdots +a_{n-1}s+a_{n}=0 \ \)が与えられている時,ラウスの安定判別法による安定条件は,
\[
\begin{eqnarray}
&&1. s^{n},s^{n-1},\cdots ,s^{1},s^{0}の係数がすべて存在 \\[ 5pt ]
&&2. s^{n},s^{n-1},\cdots ,s^{1},s^{0}の係数がすべて同符号 \\[ 5pt ]
&&3. ラウスの数表の値がすべて正であること \\[ 5pt ]
\end{eqnarray}
\]
です。ラウスの数表は下図のようになります。
\[
\begin{array}{c|ccc}
& 1列 & 2列 & 3列 \\
\hline
1行 & a_{0} & a_{2} & a_{4} & \cdots \\
2行 & a_{1} & a_{3} & a_{5} & \cdots \\
3行 & b_{1}=\frac {a_{1}a_{2}-a_{0}a_{3}}{a_{1}} & b_{2}=\frac {a_{1}a_{4}-a_{0}a_{5}}{a_{1}} & \cdots \\
4行 & c_{1}=\frac {b_{1}a_{3}-a_{1}b_{2}}{b_{1}} & c_{2}=\frac {b_{1}a_{5}-a_{1}b_{3}}{b_{1}} & \cdots \\
\vdots & \vdots & \vdots &
\end{array}
\]
3.最終値の定理
\( \ f(t) \ \)のラプラス変換を\( \ F(s) \ \)とすると,\( \ f(t) \ \)の定常値は,
\[
\begin{eqnarray}
\displaystyle \lim _{ t \to \infty } f(t)&=&\displaystyle \lim _{ s \to 0 } sF(s) \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
【解答】
(1)フィードバック制御系の特性方程式
問題図において,
\[
\begin{eqnarray}
R \left( s \right) -Y \left( s \right) &=&E \left( s \right) &・・・・・・・・ ①& \\[ 5pt ]
E \left( s \right)\cdot \frac {K}{s}\cdot \frac {100}{\left( s+1\right) \left( s+40\right) } &=&Y \left( s \right) &・・・・・・・・ ②& \\[ 5pt ]
\end{eqnarray}
\]
の関係があるから,①式を②式に代入して整理すると,
\[
\begin{eqnarray}
\left\{ R \left( s \right) -Y \left( s \right) \right\} \cdot \frac {K}{s}\cdot \frac {100}{\left( s+1\right) \left( s+40\right) } &=&Y \left( s \right) \\[ 5pt ]
\left\{ R \left( s \right) -Y \left( s \right) \right\} \cdot 100K &=&s\left( s+1\right) \left( s+40\right) Y \left( s \right) \\[ 5pt ]
100KR \left( s \right) -100KY \left( s \right) &=&\left( s^{3}+41s^{2}+40s\right) Y \left( s \right) \\[ 5pt ]
100KR \left( s \right) &=&\left( s^{3}+41s^{2}+40s+100K\right) Y \left( s \right) \\[ 5pt ]
\frac {Y \left( s \right) }{R \left( s \right) } &=&\frac {100K}{s^{3}+41s^{2}+40s+100K} \\[ 5pt ]
\end{eqnarray}
\]
となるので,特性方程式は,
\[
\begin{eqnarray}
s^{3}+41s^{2}+40s+100K&=&0 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)フィードバック制御系を安定とする\( \ K \ \)の条件
ワンポイント解説「2.ラウスの安定判別法」の通り,ラウス表を作成すると,
\[
\begin{array}{c|ccc}
& 1列 & 2列 & \\
\hline
1行 & 1 & 40 & \cdots \\
2行 & 41 & 100K & \cdots \\
3行 & \displaystyle \frac {41\times 40-1\times 100K}{41} & 0 & \cdots \\
4行 &100K & & \cdots \\
\vdots & \vdots & \vdots &
\end{array}
\]
となり,3行1列の式より,
\[
\begin{eqnarray}
\frac {41\times 40-1\times 100K}{41}&>&0 \\[ 5pt ]
1640-100K&>&0 \\[ 5pt ]
K&<&16.4 \\[ 5pt ]
\end{eqnarray}
\]
となるから,制御系が安定となる\( \ K \ \)の条件は,
\[
\begin{eqnarray}
0<K<16.4 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)目標値\( \ R \left( s \right) \ \)から制御偏差\( \ E \left( s \right) \ \)までの伝達関数\( \ T_{\mathrm {ER}} \left( s \right) \ \)
(1)で求めた関係式について②式を①式に代入すると,
\[
\begin{eqnarray}
R \left( s \right) – E \left( s \right)\cdot \frac {K}{s}\cdot \frac {100}{\left( s+1\right) \left( s+40\right) } &=&E \left( s \right) \\[ 5pt ]
R \left( s \right) -\frac {100K}{s^{3}+41s^{2}+40s} E \left( s \right) &=&E \left( s \right) \\[ 5pt ]
R \left( s \right) &=& \frac {s^{3}+41s^{2}+40s+100K}{s^{3}+41s^{2}+40s}E \left( s \right) \\[ 5pt ]
\frac {E \left( s \right) }{R \left( s \right) }&=& \frac {s^{3}+41s^{2}+40s}{s^{3}+41s^{2}+40s+100K} \\[ 5pt ]
T_{\mathrm {ER}} \left( s \right) &=& \frac {s^{3}+41s^{2}+40s}{s^{3}+41s^{2}+40s+100K} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)目標値\( \ r \left( t \right) \ \)を傾き\( \ 2 \ \)でランプ変化させたときの定常速度偏差\( \ e_{\mathrm {v}} \ \)
ワンポイント解説「1.基本的なラプラス変換」の通り,\( \ r \left( t \right) =2t \left( t≧0 \right) \ \)のラプラス変換は\( \ \displaystyle R \left( s \right) =\frac {2}{s^{2}} \ \)であり,(3)解答式より,
\[
\begin{eqnarray}
\frac {E \left( s \right) }{R \left( s \right) } &=& \frac {s^{3}+41s^{2}+40s}{s^{3}+41s^{2}+40s+100K} \\[ 5pt ]
E \left( s \right) &=& \frac {s^{3}+41s^{2}+40s}{s^{3}+41s^{2}+40s+100K}R \left( s \right) \\[ 5pt ]
&=& \frac {s^{3}+41s^{2}+40s}{s^{3}+41s^{2}+40s+100K}\cdot \frac {2}{s^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,\( \ K=2 \ \)のときの定常速度偏差\( \ e_{\mathrm {v}} \ \)は,ワンポイント解説「3.最終値の定理」の通り,
\[
\begin{eqnarray}
\displaystyle \lim _{ t \to \infty }e_{\mathrm {v}}&=&\displaystyle \lim _{ s \to 0 } sE \left( s \right) \\[ 5pt ]
&=&\displaystyle \lim _{ s \to 0 } \left( s\cdot \frac {s^{3}+41s^{2}+40s}{s^{3}+41s^{2}+40s+200}\cdot \frac {2}{s^{2}} \right) \\[ 5pt ]
&=&\displaystyle \lim _{ s \to 0 } \left( \frac {s^{2}+41s+40}{s^{3}+41s^{2}+40s+200}\times 2 \right) \\[ 5pt ]
&=&0.4 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)定常状態での制御偏差\( \ e \left( t \right) \ \)が\( \ B \sin \left( t+\theta \right) \ \)で表される正弦関数となったときの\( \ B \ \)の値
\( \ K=2 \ \)のときの伝達関数\( \ T_{\mathrm {ER}} \left( s \right) \ \)の周波数伝達関数\( \ T_{\mathrm {ER}} \left( \mathrm {j}\omega \right) \ \)は,
\[
\begin{eqnarray}
T_{\mathrm {ER}} \left( \mathrm {j}\omega \right) &=& \frac {\left( \mathrm {j}\omega \right) ^{3}+41\left( \mathrm {j}\omega \right) ^{2}+40\left( \mathrm {j}\omega \right) }{\left( \mathrm {j}\omega \right) ^{3}+41\left( \mathrm {j}\omega \right) ^{2}+40\left( \mathrm {j}\omega \right) +200} \\[ 5pt ]
&=& \frac {-41\omega ^{2}+\mathrm {j}\left( 40\omega -\omega ^{3}\right) }{200-41\omega ^{2}+\mathrm {j}\left( 40\omega -\omega ^{3}\right) } \\[ 5pt ]
\end{eqnarray}
\]
であり,題意より目標値\( \ r \left( t \right) = 2\sin t \ \)なので,\( \ \omega =1 \ \)であるから,
\[
\begin{eqnarray}
T_{\mathrm {ER}} \left( \mathrm {j}\omega \right) &=& \frac {-41+\mathrm {j}39 }{159+\mathrm {j}39 } \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,ゲイン\( \ \left| T_{\mathrm {ER}} \left( \mathrm {j}\omega \right) \right| \ \)は,
\[
\begin{eqnarray}
\left| T_{\mathrm {ER}} \left( \mathrm {j}\omega \right) \right| &=& \left| \frac {-41+\mathrm {j}39 }{159+\mathrm {j}39 }\right| \\[ 5pt ]
&=& \sqrt {\frac {41^{2}+39^{2} }{159^{2}+39^{2} }} \\[ 5pt ]
&=& \sqrt {\frac {3202}{26802}} \\[ 5pt ]
&≒& 0.34564 \\[ 5pt ]
\end{eqnarray}
\]
となるので,目標値\( \ r \left( t \right) = 2\sin t \ \)の振幅は\( \ 2 \ \)であるから,
\[
\begin{eqnarray}
B &=&\left| T_{\mathrm {ER}} \left( \mathrm {j}\omega \right) \right| \times 2 \\[ 5pt ]
&=& 0.34564\times 2 \\[ 5pt ]
&≒& 0.691 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは