《電力・管理》〈送電〉[R04:問3]単位法を用いた調相設備の容量の導出に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

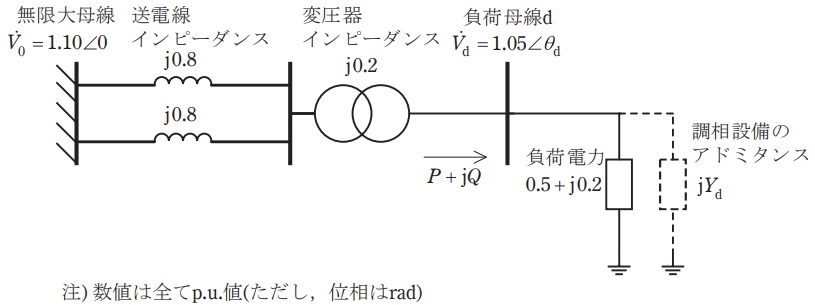
送電線により受電する下図の負荷母線\( \ \mathrm {d} \ \)の受電電圧\( \ V_{\mathrm {d}} \ \)を\( \ 1.05 \ \mathrm {p.u.} \ \)に維持するために必要な調相設備(コンデンサあるいはリアクトル)のサセプタンス\( \ Y_{\mathrm {d}} \ \)を，単位法を用いて，以下の手順で求める。それぞれの問に答えよ。なお，遅れ無効電力を正とする。

(1)　負荷母線\( \ \mathrm {d} \ \)に到達する有効電力\( \ P \ \)に関する数式を用いて，\( \ \sin \theta _{\mathrm {d}} \ \)の値を求めよ。

(2)　負荷母線\( \ \mathrm {d} \ \)に到達する遅れ無効電力\( \ Q \ \)を\( \ \cos \theta _{\mathrm {d}} \ \)の関数で表せ。

(3)　上記小問(2)の解を用いて必要調相設備サセプタンス\( \ Y_{\mathrm {d}} \ \)を\( \ \cos \theta _{\mathrm {d}} \ \)の関数で表せ。

(4)　上記の各小問の解を用いて必要調相設備サセプタンス\( \ Y_{\mathrm {d}} \ \)を求めよ。ただし，\( \ \displaystyle \left| \theta _{\mathrm {d}}\right| ＜\frac {\pi }{2} \ \)とする。

【ワンポイント解説】

単位法を用いた電力の演算や調相設備の容量を求める問題です。
少し計算量が多い部分があったため，令和４年度の計算問題の中では最も難易度が高かった問題かと思います。
(1)の複素電力を指数関数表記にて求める計算方法は重要な内容となりますので，この問題で理解するようにしましょう。

1.オーム法から単位法への変換
基準容量を\( \ P_{\mathrm {n}} \ \mathrm {[V\cdot A]} \ \)，基準電圧を\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \)，基準電流を\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)とすると，
\[
\begin{eqnarray}
Z \ \mathrm {[p.u.]} \ &=&\frac {Z \ \mathrm {[\Omega ]} \ I_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}　　 (定義) \\[ 5pt ] &=&\frac {\sqrt {3}Z \ \mathrm {[\Omega ]} \ I_{\mathrm {n}}}{V_{\mathrm {n}}} \\[ 5pt ] &=&\frac {\sqrt {3}Z \ \mathrm {[\Omega ]} \ V_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}} \\[ 5pt ] &=&\frac {P_{\mathrm {n}}Z \ \mathrm {[\Omega ]} \ }{V_{\mathrm {n}}^{2}}　　 (∵P_{\mathrm {n}}=\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} ) \\[ 5pt ] \end{eqnarray}
\] となります。

2.複素電力
電圧\( \ \dot V \ \mathrm {[V]} \)，電流\( \ \dot I \ \mathrm {[A]} \ \)とした時，送電線の送電電力\( \ \dot S=P+\mathrm {j}Q \ \mathrm {[V\cdot A]} \ \)は，
遅れ無効電力を正とすると，
\[
\begin{eqnarray}
\dot S=P+\mathrm {j}Q&=&\dot V \overline {\dot I} \\[ 5pt ] \end{eqnarray}
\] 進み無効電力を正とすると，
\[
\begin{eqnarray}
\dot S=P+\mathrm {j}Q&=&\overline {\dot V}\dot I \\[ 5pt ] \end{eqnarray}
\] で求められます。

※　一般に遅れ無効電力を正とする場合が多いので，上の式を基本として覚えておきましょう。

【解答】

(1)\( \ \sin \theta _{\mathrm {d}} \ \)の値
無限大母線と負荷母線\( \ \mathrm {d} \ \)の間の合成リアクタンス\( \ \mathrm {j}X \ \mathrm {[p.u.]} \ \)は，
\[
\begin{eqnarray}
\mathrm {j}X&=&\frac {\mathrm {j}0.8\times \mathrm {j}0.8}{\mathrm {j}0.8+\mathrm {j}0.8}+\mathrm {j}0.2 \\[ 5pt ] &=&\mathrm {j}0.6 \ \mathrm {[p.u.]} \\[ 5pt ] \end{eqnarray}
\] であるため，負荷電流\( \ \dot I \ \mathrm {[p.u.]} \ \)は，
\[
\begin{eqnarray}
\dot I&=&\frac {{\dot V}_{0}-{\dot V}_{\mathrm {d}}}{\mathrm {j}X} \\[ 5pt ] &=&\frac {1.10-1.05\mathrm {e}^{\mathrm {j}\theta _{\mathrm {d}}} }{\mathrm {j}0.6} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，負荷母線に到達する電力\( \ P+\mathrm {j}Q \ \mathrm {[p.u.]} \ \)は，ワンポイント解説「2.複素電力」の通り，
\[
\begin{eqnarray}
P+\mathrm {j}Q&=&{\dot V}_{\mathrm {d}} \overline {\dot I} \\[ 5pt ] &=&1.05\mathrm {e}^{\mathrm {j}\theta _{\mathrm {d}}} \cdot \frac {1.10-1.05\mathrm {e}^{-\mathrm {j}\theta _{\mathrm {d}}} }{-\mathrm {j}0.6} \\[ 5pt ] &=&\mathrm {j}\frac {1.05}{0.6}\left( 1.10\mathrm {e}^{\mathrm {j}\theta _{\mathrm {d}}}-1.05 \right) \\[ 5pt ] &=&\mathrm {j}1.925\mathrm {e}^{\mathrm {j}\theta _{\mathrm {d}}}-\mathrm {j}1.8375 \\[ 5pt ] &=&\mathrm {j}1.925\left( \cos \theta _{\mathrm {d}} +\mathrm {j}\sin \theta _{\mathrm {d}} \right) -\mathrm {j}1.8375 \\[ 5pt ] &=&-1.925\sin \theta _{\mathrm {d}}+\mathrm {j}\left( 1.925\cos \theta _{\mathrm {d}}-1.8375 \right) 　・・・・・・　① \\[ 5pt ] \end{eqnarray}
\] となる。問題図より，負荷の有効電力\( \ P=0.5 \ \mathrm {[p.u.]} \ \)であるから，
\[
\begin{eqnarray}
P&=&-1.925\sin \theta _{\mathrm {d}} \\[ 5pt ] 0.5&=&-1.925\sin \theta _{\mathrm {d}} \\[ 5pt ] \sin \theta _{\mathrm {d}}&≒&-0.25974　→　-0.260 \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)遅れ無効電力\( \ Q \ \)を\( \ \cos \theta _{\mathrm {d}} \ \)の関数で表す
①式より，
\[
\begin{eqnarray}
Q&=&1.925\cos \theta _{\mathrm {d}}-1.8375　→　1.93\cos \theta _{\mathrm {d}}-1.84 \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)必要調相設備サセプタンス\( \ Y_{\mathrm {d}} \ \)を\( \ \cos \theta _{\mathrm {d}} \ \)の関数で表す
調相サセプタンスの容量を\( \ Q_{\mathrm {C}} \ \)とすると，
\[
\begin{eqnarray}
Q_{\mathrm {C}}&=&Y_{\mathrm {d}}\left| {\dot V}_{\mathrm {d}}\right| ^{2} \\[ 5pt ] &=&Y_{\mathrm {d}}\cdot 1.05^{2} \\[ 5pt ] &=&1.1025Y_{\mathrm {d}} \\[ 5pt ] \end{eqnarray}
\] となるので，\( \ Q_{\mathrm {C}} \ \)と負荷電力を合成したものが(2)で求めた\( \ Q \ \)と等しいことから，
\[
\begin{eqnarray}
Q&=&0.2-Q_{\mathrm {C}} \\[ 5pt ] 1.925\cos \theta _{\mathrm {d}}-1.8375&=&0.2-1.1025Y_{\mathrm {d}} \\[ 5pt ] 1.1025Y_{\mathrm {d}}&=&2.0375-1.925\cos \theta _{\mathrm {d}} \\[ 5pt ] Y_{\mathrm {d}}&≒&1.8481-1.7460\cos \theta _{\mathrm {d}}　→　1.85-1.75\cos \theta _{\mathrm {d}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)必要調相設備サセプタンス\( \ Y_{\mathrm {d}} \ \)を求める
(1)より，\( \ \sin \theta _{\mathrm {d}}=-0.25974 \ \)であるから，
\[
\begin{eqnarray}
\cos \theta _{\mathrm {d}}&=&\sqrt {1-\sin ^{2}\theta _{\mathrm {d}}} \\[ 5pt ] &=&\sqrt {1-\left( -0.25974\right) ^{2}} \\[ 5pt ] &≒&0.96568 \\[ 5pt ] \end{eqnarray}
\] となり，これを(3)解答式に代入すると，
\[
\begin{eqnarray}
Y_{\mathrm {d}}&=&1.8481-1.7460\cos \theta _{\mathrm {d}} \\[ 5pt ] &=&1.8481-1.7460\times 0.96568 \\[ 5pt ] &≒&0.162 \ \mathrm {[p.u.]} \\[ 5pt ] \end{eqnarray}
\] と求められる。