《電力・管理》〈電気施設管理〉[R04:問6]需要設備の需要率，不等率，負荷率に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

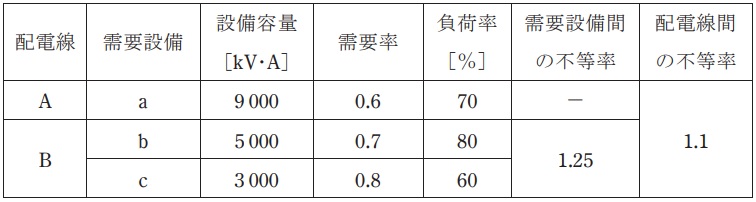
ある変電所から，配電線\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)により，下表に示す需要設備\( \ \mathrm {a} \ \)，\( \ \mathrm {b} \ \)，\( \ \mathrm {c} \ \)に電力を供給しているとき，次の問に答えよ。配電線は\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)以外にはないものとし，需要設備\( \ \mathrm {a} \ \)，\( \ \mathrm {b} \ \)，\( \ \mathrm {c} \ \)の力率は全て\( \ 90 \ \mathrm {％} \ \) (遅れ一定)とする。

(1)　需要設備\( \ \mathrm {a} \ \)，\( \ \mathrm {b} \ \)，\( \ \mathrm {c} \ \)の最大電力\( \ \mathrm {[kW]} \ \)をそれぞれ求めよ。

(2)　変電所の総合最大電力\( \ \mathrm {[kW]} \ \)を求めよ。

(3)　需要設備\( \ \mathrm {a} \ \)，\( \ \mathrm {b} \ \)，\( \ \mathrm {c} \ \)の平均電力\( \ \mathrm {[kW]} \ \)をそれぞれ求めよ。

(4)　変電所の総合負荷率\( \ \mathrm {[％]} \ \)を求めよ。

【ワンポイント解説】

変電所から需要設備に向かう電路の電力計算に関する問題です。
需要率，不等率，負荷率の定義式は忘れやすいので，試験前に必ず再確認しておくようにしましょう。
本問は平成27年電力管理問5にほぼ同じ問題が出題されているので，多くの受験生が正答したと予想されます。

1.需要率，不等率，負荷率の定義
①需要率
\[
\begin{eqnarray}
需要率&=&\frac {最大需要電力}{設備容量}\times 100　[％] \\[ 5pt ] \end{eqnarray}
\]

②不等率（常に1以上となる)
\[
\begin{eqnarray}
不等率&=&\frac {各最大需要電力の和}{合成した最大需要電力} \\[ 5pt ] \end{eqnarray}
\]

③負荷率
\[
\begin{eqnarray}
負荷率&=&\frac {平均需要電力}{最大需要電力}\times 100　[％] \\[ 5pt ] \end{eqnarray}
\]

【解答】

(1)需要設備\( \ \mathrm {a} \ \)，\( \ \mathrm {b} \ \)，\( \ \mathrm {c} \ \)の最大電力\( \ \mathrm {[kW]} \ \)
需要設備\( \ \mathrm {a} \ \)，\( \ \mathrm {b} \ \)，\( \ \mathrm {c} \ \)の最大電力をそれぞれ\( \ P_{\mathrm {ma}} \ \mathrm {[kW]} \ \)，\( \ P_{\mathrm {mb}} \ \mathrm {[kW]} \ \)，\( \ P_{\mathrm {mc}} \ \mathrm {[kW]} \ \)とすると，力率\( \ \cos \theta =0.9 \ \)であるから，ワンポイント解説「1.需要率，不等率，負荷率の定義」より，
\[
\begin{eqnarray}
P_{\mathrm {ma}}&=&{設備容量}_{\mathrm {a}}\times {需要率}_{\mathrm {a}}\times \cos \theta \\[ 5pt ] &=&9 \ 000\times 0.6\times 0.9 \\[ 5pt ] &=&4 \ 860 \ \mathrm {[kW]} \\[ 5pt ] P_{\mathrm {mb}}&=&{設備容量}_{\mathrm {b}}\times {需要率}_{\mathrm {b}}\times \cos \theta \\[ 5pt ] &=&5 \ 000\times 0.7\times 0.9 \\[ 5pt ] &=&3 \ 150 \ \mathrm {[kW]} \\[ 5pt ] P_{\mathrm {mc}}&=&{設備容量}_{\mathrm {c}}\times {需要率}_{\mathrm {c}}\times \cos \theta \\[ 5pt ] &=&3 \ 000\times 0.8\times 0.9 \\[ 5pt ] &=&2 \ 160 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)変電所の総合最大電力\( \ \mathrm {[kW]} \ \)
配電線\( \ \mathrm {B} \ \)の最大電力を\( \ P_{\mathrm {mB}} \ \mathrm {[kW]} \ \)とすると，ワンポイント解説「1.需要率，不等率，負荷率の定義」より，
\[
\begin{eqnarray}
需要設備間の不等率&=&\frac {P_{\mathrm {mb}}+P_{\mathrm {mc}}}{P_{\mathrm {mB}}} \\[ 5pt ] 1.25&=&\frac {3 \ 150+2 \ 160}{P_{\mathrm {mB}}} \\[ 5pt ] P_{\mathrm {mB}}&=&\frac {3 \ 150+2 \ 160}{1.25} \\[ 5pt ] &=&4 \ 248 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] であるので，変電所の総合最大電力\( \ P_{\mathrm {m}} \ \mathrm {[kW]} \ \)は，
\[
\begin{eqnarray}
配電線間の不等率&=&\frac {P_{\mathrm {ma}}+P_{\mathrm {mB}}}{P_{\mathrm {m}}} \\[ 5pt ] 1.1&=&\frac {4 \ 860+4 \ 248}{P_{\mathrm {m}}} \\[ 5pt ] P_{\mathrm {m}}&=&\frac {4 \ 860+4 \ 248}{1.1} \\[ 5pt ] &=&8 \ 280 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)需要設備\( \ \mathrm {a} \ \)，\( \ \mathrm {b} \ \)，\( \ \mathrm {c} \ \)の平均電力\( \ \mathrm {[kW]} \ \)
需要設備\( \ \mathrm {a} \ \)，\( \ \mathrm {b} \ \)，\( \ \mathrm {c} \ \)の平均電力をそれぞれ\( \ P_{\mathrm {a}} \ \mathrm {[kW]} \ \)，\( \ P_{\mathrm {b}} \ \mathrm {[kW]} \ \)，\( \ P_{\mathrm {c}} \ \mathrm {[kW]} \ \)とすると，ワンポイント解説「1.需要率，不等率，負荷率の定義」より，
\[
\begin{eqnarray}
P_{\mathrm {a}}&=&P_{\mathrm {ma}}\times {負荷率}_{\mathrm {a}} \\[ 5pt ] &=&4 \ 860\times 0.7 \\[ 5pt ] &=&3 \ 402　→　3 \ 400 \ \mathrm {[kW]} \\[ 5pt ] P_{\mathrm {b}}&=&P_{\mathrm {mb}}\times {負荷率}_{\mathrm {b}} \\[ 5pt ] &=&3 \ 150\times 0.8 \\[ 5pt ] &=&2 \ 520 \ \mathrm {[kW]} \\[ 5pt ] P_{\mathrm {c}}&=&P_{\mathrm {mc}}\times {負荷率}_{\mathrm {c}} \\[ 5pt ] &=&2 \ 160\times 0.6 \\[ 5pt ] &=&1 \ 296　→　1 \ 300 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)変電所の総合負荷率\( \ \mathrm {[％]} \ \)
(2)，(3)より，総合負荷率\( \ LF \ \mathrm {[％]} \ \)は，ワンポイント解説「1.需要率，不等率，負荷率の定義」の通り，
\[
\begin{eqnarray}
LF&=&\frac {P_{\mathrm {a}}+P_{\mathrm {b}}+P_{\mathrm {c}}}{P_{\mathrm {m}}}\times 100 \\[ 5pt ] &=&\frac {3 \ 402+2 \ 520+1 \ 296}{8 \ 280}\times 100 \\[ 5pt ] &≒&87.2 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。