Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
図に示す中性点接地方式の架空送電系統において故障点\( \ \mathrm {F} \ \)で\( \ \mathrm {a} \ \)相の\( \ 1 \ \)線地絡事故が発生した。次の問に答えよ。
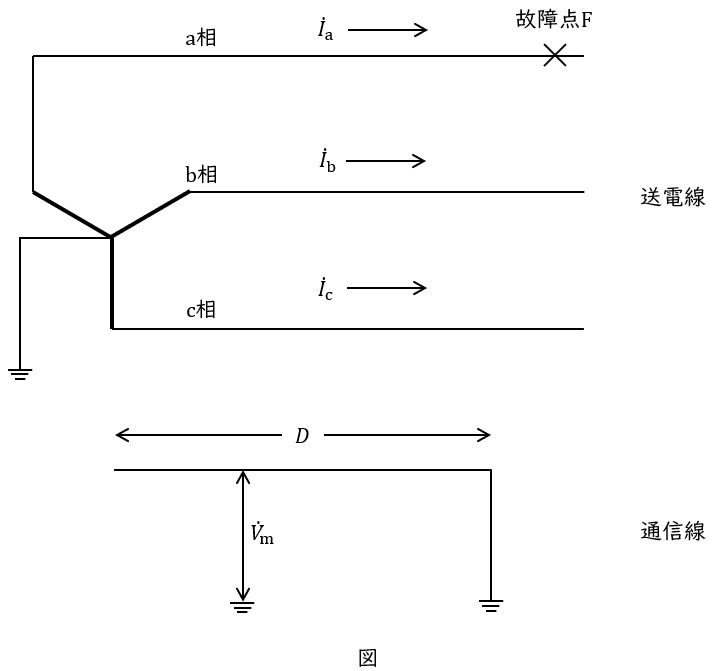
(1) \( \ 1 \ \)線地絡電流\( \ {\dot I}_{\mathrm {a}} \ \)を零相電流\( \ {\dot I}_{\mathrm {0}} \ \)を用いて表せ。なお,送電線は無負荷とする。
(2) 電磁誘導により通信線に発生する誘導電圧\( \ {\dot V}_{\mathrm {m}} \ \mathrm {[V]} \ \)の大きさ\( \ \left| {\dot V}_{\mathrm {m}} \right| \ \)を,小問(1)の\( \ {\dot I}_{\mathrm {0}} \ \),周波数\( \ f \ \mathrm {[Hz]} \ \),送電線と通信線との相互インダクタンス\( \ M \ \mathrm {[H / km]} \ \),送電線と通信線が並行している距離\( \ D \ \mathrm {[km]} \ \),及び\( \ \pi \ \)を用いて表せ。
(3) \( \ M \ \)が\( \ 5.0 \ \mathrm {mH / km} \ \),\( \ D \ \)が\( \ 0.8 \ \mathrm {km} \ \)の場合,\( \ \left| {\dot V}_{\mathrm {m}} \right| \ \)を\( \ 430 \ \mathrm {V} \ \)以下とするための\( \ {\dot I}_{\mathrm {a}} \ \mathrm {[A]} \ \)の大きさ\( \ \left| {\dot I}_{\mathrm {a}} \right| \ \)の上限値を求めよ。なお,\( \ f=50 \ \mathrm {Hz} \ \),\( \ \pi =3.14 \ \)とする。
【ワンポイント解説】
\( \ 1 \ \)線地絡事故発生時に通信線に発生する誘導電圧に関する問題です。
本問は計算問題ですが,電磁誘導障害に関しては論述問題として出題される可能性もあり,近年では2種電力管理科目令和2年問5に出題されています。本問を理解した後勉強するととても効果的と思いますので,ぜひ一緒に学習するようにしてみて下さい。
また,かなり古い過去問ですが,平成9年問3に類題が出題されていましたので,過去問学習をされた方は得点できた可能性が高いかと思います。
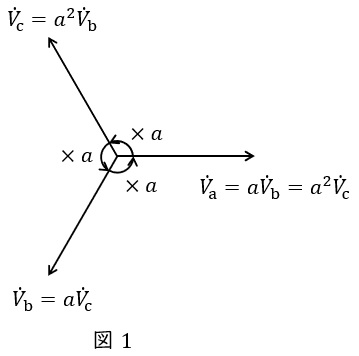
1.ベクトルオペレータ\( \ a \ \)
ベクトルオペレータとは,\( \ a=\mathrm {e}^{\mathrm {j}\frac {2\pi}{3}} \ \)で定義される演算子であり,
\[
\begin{eqnarray}
a &=& \cos \frac {2\pi}{3}+\mathrm {j}\sin \frac {2\pi}{3} \\[ 5pt ]
&=& -\frac {1}{2}+\mathrm {j}\frac {\sqrt {3}}{2} \\[ 5pt ]
a^{2} &=& \cos \frac {4\pi}{3}+\mathrm {j}\sin \frac {4\pi}{3} \\[ 5pt ]
&=& -\frac {1}{2}-\mathrm {j}\frac {\sqrt {3}}{2} \\[ 5pt ]
a^{3} &=& \cos \frac {6\pi}{3}+\mathrm {j}\sin \frac {6\pi}{3} \\[ 5pt ]
&=& 1 \\[ 5pt ]
\end{eqnarray}
\]
という関係があります。
2.対称座標法
故障計算をする際に,非常に便利な方法で,零相電圧\( \ {\dot V}_{0} \ \),正相電圧\( \ {\dot V}_{1} \ \),逆相電圧\( \ {\dot V}_{2} \ \)とすると,各相の電圧\( \ {\dot V}_{\mathrm {a}} \ \),\( \ {\dot V}_{\mathrm {b}} \ \),\( \ {\dot V}_{\mathrm {c}} \ \)を用いて以下のように定義されます。ただし,\( \ a \ \)はベクトルオペレータとなります。
\[
\begin{eqnarray}
{\dot V}_{\mathrm {0}} &=&\frac {1}{3}\left( {\dot V}_{\mathrm {a}}+ {\dot V}_{\mathrm {b}} + {\dot V}_{\mathrm {c}}\right) \\[ 5pt ]
{\dot V}_{\mathrm {1}} &=&\frac {1}{3}\left( {\dot V}_{\mathrm {a}}+ a{\dot V}_{\mathrm {b}} + a^{2}{\dot V}_{\mathrm {c}}\right) \\[ 5pt ]
{\dot V}_{\mathrm {2}} &=&\frac {1}{3}\left( {\dot V}_{\mathrm {a}}+ a^{2}{\dot V}_{\mathrm {b}} + a{\dot V}_{\mathrm {c}}\right) \\[ 5pt ]
\end{eqnarray}
\]
このとき,各相の電圧\( \ {\dot V}_{\mathrm {a}} \ \),\( \ {\dot V}_{\mathrm {b}} \ \),\( \ {\dot V}_{\mathrm {c}} \ \)は以下のように表せます。
\[
\begin{eqnarray}
{\dot V}_{\mathrm {a}} &=&{\dot V}_{0}+ {\dot V}_{1} + {\dot V}_{2} \\[ 5pt ]
{\dot V}_{\mathrm {b}} &=&{\dot V}_{0}+ a^{2}{\dot V}_{1} + a{\dot V}_{2} \\[ 5pt ]
{\dot V}_{\mathrm {c}} &=&{\dot V}_{0}+ a{\dot V}_{1} + a^{2}{\dot V}_{2} \\[ 5pt ]
\end{eqnarray}
\]
なお,図1に示すような三相平衡時においては,\( \ {\dot V}_{\mathrm {a}}+{\dot V}_{\mathrm {b}}+{\dot V}_{\mathrm {c}}=0 \ \)であるため,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {0}} &=&\frac {1}{3}\left( {\dot V}_{\mathrm {a}}+ {\dot V}_{\mathrm {b}} + {\dot V}_{\mathrm {c}}\right) \\[ 5pt ]
&=&0 \\[ 5pt ]
{\dot V}_{\mathrm {1}} &=&\frac {1}{3}\left( {\dot V}_{\mathrm {a}}+ a{\dot V}_{\mathrm {b}} + a^{2}{\dot V}_{\mathrm {c}}\right) \\[ 5pt ]
&=&\frac {1}{3}\left( {\dot V}_{\mathrm {a}}+ {\dot V}_{\mathrm {a}} + {\dot V}_{\mathrm {a}}\right) \\[ 5pt ]
&=&{\dot V}_{\mathrm {a}} \\[ 5pt ]
{\dot V}_{\mathrm {2}} &=&\frac {1}{3}\left( {\dot V}_{\mathrm {a}}+ a^{2}{\dot V}_{\mathrm {b}} + a{\dot V}_{\mathrm {c}}\right) \\[ 5pt ]
&=&\frac {1}{3}\left( {\dot V}_{\mathrm {a}}+ {\dot V}_{\mathrm {c}} + {\dot V}_{\mathrm {b}}\right) \\[ 5pt ]
&=&0 \\[ 5pt ]
\end{eqnarray}
\]
となります。
同様に,零相電流\( \ {\dot I}_{0} \ \),正相電流\( \ {\dot I}_{1} \ \),逆相電流\( \ {\dot I}_{2} \ \)とすると,各相の電流\( \ {\dot I}_{\mathrm {a}} \ \),\( \ {\dot I}_{\mathrm {b}} \ \),\( \ {\dot I}_{\mathrm {c}} \ \)を用いて以下のように定義されます。
\[
\begin{eqnarray}
{\dot I}_{\mathrm {0}} &=&\frac {1}{3}\left( {\dot I}_{\mathrm {a}}+ {\dot I}_{\mathrm {b}} + {\dot I}_{\mathrm {c}}\right) \\[ 5pt ]
{\dot I}_{\mathrm {1}} &=&\frac {1}{3}\left( {\dot I}_{\mathrm {a}}+ a{\dot I}_{\mathrm {b}} + a^{2}{\dot I}_{\mathrm {c}}\right) \\[ 5pt ]
{\dot I}_{\mathrm {2}} &=&\frac {1}{3}\left( {\dot I}_{\mathrm {a}}+ a^{2}{\dot I}_{\mathrm {b}} + a{\dot I}_{\mathrm {c}}\right) \\[ 5pt ]
\end{eqnarray}
\]
このとき,各相の電流\( \ {\dot I}_{\mathrm {a}} \ \),\( \ {\dot I}_{\mathrm {b}} \ \),\( \ {\dot I}_{\mathrm {c}} \ \)は以下のように表せます。
\[
\begin{eqnarray}
{\dot I}_{\mathrm {a}} &=&{\dot I}_{0}+ {\dot I}_{1} + {\dot I}_{2} \\[ 5pt ]
{\dot I}_{\mathrm {b}} &=&{\dot I}_{0}+ a^{2}{\dot I}_{1} + a{\dot I}_{2} \\[ 5pt ]
{\dot I}_{\mathrm {c}} &=&{\dot I}_{0}+ a{\dot I}_{1} + a^{2}{\dot I}_{2} \\[ 5pt ]
\end{eqnarray}
\]
また,対称座標法における零相インピーダンス\( \ {\dot Z}_{\mathrm {0}} \ \),正相インピーダンス\( \ {\dot Z}_{\mathrm {1}} \ \),逆相インピーダンス\( \ {\dot Z}_{\mathrm {2}} \ \),\( \ \mathrm {a} \ \)相の無負荷電圧\( \ {\dot E}_{\mathrm {a}} \ \)としたとき,発電機の基本式は以下の通りとなります。
\[
\begin{eqnarray}
{\dot V}_{0} &=&-{\dot Z}_{0}{\dot I}_{0} \\[ 5pt ]
{\dot V}_{1} &=&{\dot E}_{\mathrm {a}}-{\dot Z}_{1}{\dot I}_{1} \\[ 5pt ]
{\dot V}_{2} &=&-{\dot Z}_{2}{\dot I}_{2} \\[ 5pt ]
\end{eqnarray}
\]
これらの式を利用して,事故電流の大きさを求めます。
【解答】
(1)\( \ 1 \ \)線地絡電流\( \ {\dot I}_{\mathrm {a}} \ \)を零相電流\( \ {\dot I}_{\mathrm {0}} \ \)を用いて表す
送電線が無負荷で完全地絡しているとき,\( \ {\dot I}_{\mathrm {b}}={\dot I}_{\mathrm {c}}=0 \ \mathrm {[A]} \ \)であるから,\( \ 1 \ \)線地絡電流\( \ {\dot I}_{\mathrm {a}} \ \)は,ワンポイント解説「2.対称座標法」の通り,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {0}} &=&\frac {1}{3}\left( {\dot I}_{\mathrm {a}}+ {\dot I}_{\mathrm {b}} + {\dot I}_{\mathrm {c}}\right) \\[ 5pt ]
&=&\frac {1}{3}{\dot I}_{\mathrm {a}} \\[ 5pt ]
{\dot I}_{\mathrm {a}}&=&3{\dot I}_{\mathrm {0}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)電磁誘導により通信線に発生する誘導電圧\( \ {\dot V}_{\mathrm {m}} \ \mathrm {[V]} \ \)の大きさ\( \ \left| {\dot V}_{\mathrm {m}} \right| \ \)
送電線と通信線との相互インダクタンスは\( \ MD \ \mathrm {[H]} \ \)であり,一般に電流\( \ \dot I \ \mathrm {[A]} \ \)により誘導される誘導電圧\( \ \dot V \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
\dot V &=&\mathrm {j}\omega MD \dot I \\[ 5pt ]
\end{eqnarray}
\]
であるから,三相電流により通信線に発生する誘導電圧\( \ {\dot V}_{\mathrm {m}} \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {m}} &=&\mathrm {j}\omega MD {\dot I}_{\mathrm {a}}+\mathrm {j}\omega MD {\dot I}_{\mathrm {b}}+\mathrm {j}\omega MD {\dot I}_{\mathrm {c}} \\[ 5pt ]
&=&\mathrm {j}\omega MD \left( {\dot I}_{\mathrm {a}}+ {\dot I}_{\mathrm {b}}+{\dot I}_{\mathrm {c}}\right) \\[ 5pt ]
&=&\mathrm {j}2\pi f MD \cdot 3{\dot I}_{\mathrm {0}} \\[ 5pt ]
&=&\mathrm {j}6\pi f MD {\dot I}_{\mathrm {0}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,その大きさ\( \ \left| {\dot V}_{\mathrm {m}}\right| \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
\left| {\dot V}_{\mathrm {m}}\right| &=&\left| \mathrm {j}6\pi f MD {\dot I}_{\mathrm {0}}\right| \\[ 5pt ]
&=&6\pi f MD \left| {\dot I}_{\mathrm {0}}\right| \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)\( \ \left| {\dot V}_{\mathrm {m}} \right| \ \)を\( \ 430 \ \mathrm {V} \ \)以下とするための\( \ {\dot I}_{\mathrm {a}} \ \mathrm {[A]} \ \)の大きさ\( \ \left| {\dot I}_{\mathrm {a}} \right| \ \)の上限値
(2)解答式より,
\[
\begin{eqnarray}
\left| {\dot I}_{\mathrm {0}}\right| &=&\frac {\left| {\dot V}_{\mathrm {m}}\right| }{6\pi f MD} \\[ 5pt ]
\frac {\left| {\dot I}_{\mathrm {a}}\right| }{3}&=&\frac {\left| {\dot V}_{\mathrm {m}}\right| }{6\pi f MD} \\[ 5pt ]
\left| {\dot I}_{\mathrm {a}}\right| &=&\frac {\left| {\dot V}_{\mathrm {m}}\right| }{2\pi f MD} \\[ 5pt ]
\end{eqnarray}
\]
であるから,各値を代入すると,
\[
\begin{eqnarray}
\left| {\dot I}_{\mathrm {a}}\right| &=&\frac {430}{2\times 3.14\times 50\times 5.0\times 10^{-3}\times 0.8} \\[ 5pt ]
&≒&342 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは