《機械》〈回転機〉[H26:問2]単相誘導電動機に関する空欄穴埋問題

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，単相誘導電動機に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選びなさい。

家庭用電気機器や小形作業機械など，三相電源がない場合に使用される単相誘導電動機は，固定子に単相巻線を施し，回転子はかご形にした構造の電動機である。

この単相巻線に交流電圧を加えると，交番磁束が発生する。この交番磁束は同期角速度\( \ \omega _{\mathrm {s}} \ \)で互いに反対方向に回転する二つの回転磁束\( \ \phi _{\mathrm {f}} \ \)及び\( \ \phi _{\mathrm {b}} \ \)に分解することができる。各回転磁束の大きさは交番磁束の最大値の\( \ \fbox {　 （１） 　} \ \)倍である。

いま，回転子が無負荷の状態において角速度\( \ \omega \ \)で正回転しているとき，正方向の回転磁束\( \ \phi _{\mathrm {f}} \ \)に対する滑りを\( \ s \ \)とすると，普通の多相誘導電動機の場合と同様に滑り\( \ s \ \)は，\( \ \omega _{\mathrm {s}} \ \)及び\( \ \omega \ \)を用いて表すと次式となる。
\[
s=\frac {\omega _{\mathrm {s}}-\omega }{\omega _{\mathrm {s}}}　　　・・・・・・・・・・・・・　①
\] 同様にして，逆方向の回転磁束\( \ \phi _{\mathrm {b}} \ \)に対する滑り\( \ s^{\prime } \ \)は，\( \ \omega _{\mathrm {s}} \ \)及び\( \ \omega \ \)を用いて表すと次式となる。
\[
s^{\prime }=\fbox {　 （２） 　}　　　・・・・・・・・・・・・・　②
\] したがって，①，②式によって\(s^{\prime }\)は，\(s\)を用いて表すと
\[
s^{\prime }=\fbox {　 （３） 　}
\] となる。

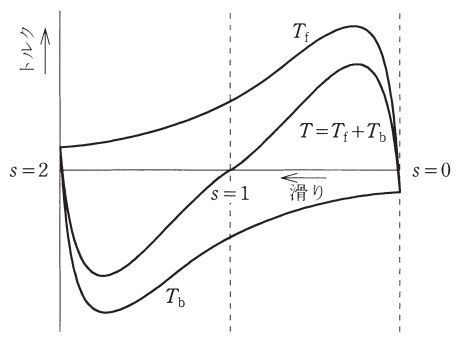
\( \ \phi _{\mathrm {f}} \ \)によって生じるトルクを\( \ T_{\mathrm {f}} \ \)，\( \ \phi _{\mathrm {b}} \ \)によって生じるトルクを\( \ T _{\mathrm {b}} \ \)とすれば，両トルクは図に示すように，\( \ s=1 \ \)の点を対象の中心として互いに点対称のトルク特性となる。単相誘導電動機のトルク特性は，両トルクを合成した\( \ T=T _{\mathrm {f}}+T _{\mathrm {b}} \ \)となる。この図から分かるように，\( \ \fbox {　 （４） 　} \ \)時には始動トルクは生じないが，正方向又は逆方向のいずれかの方向に何らかの方法でわずかでも回転させるとその方向にトルクを生じて\( \ \fbox {　 （５） 　} \ \)付近まで加速して運転を続ける。

〔問2の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {1}{\sqrt {2}}　　　　　&（ロ）&　\frac {\omega _{\mathrm {s}}+\omega }{\omega _{\mathrm {s}}}　　　　　&（ハ）&　逆回転 \\[ 5pt ] &（ニ）&　最小トルク　　　　　&（ホ）&　s+1　　　　　&（ヘ）&　正回転 \\[ 5pt ] &（ト）&　\frac {1}{2}　 　　　&（チ）&　静止　　　　　&（リ）&　-s \\[ 5pt ] &（ヌ）&　2　　　　　&（ル）&　2-s　　　　　&（ヲ）&　\frac {2\omega _{\mathrm {s}}-\omega }{\omega _{\mathrm {s}}} \\[ 5pt ] &（ワ）&　\frac {\omega -\omega _{\mathrm {s}} }{\omega _{\mathrm {s}}}　　　　　&（カ）&　同期速度　　 　　&（ヨ）&　最大トルク \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

この誘導電動機の問題はそのまま一種の問題として出題されても違和感がないくらい細かい問題と言えます。(2)を間違えると(3)も間違えてしまうのでなかなか厳しい問題と言えると思います。ただし，(4)及び(5)は基本問題となるので取りこぼしは避けたいところです。

1.加法定理
\(\sin \)と\(\cos \)の加法定理は高校の数学で習いますが電験では基本公式として扱います。
\[
\begin{eqnarray}
\sin \left( \alpha ± \beta \right) &=& \sin \alpha \cos \beta ±\cos \alpha \sin \beta \\[ 5pt ] \cos \left( \alpha ± \beta \right) &=& \cos \alpha \cos \beta ∓\sin \alpha \sin \beta \\[ 5pt ] \end{eqnarray}
\]

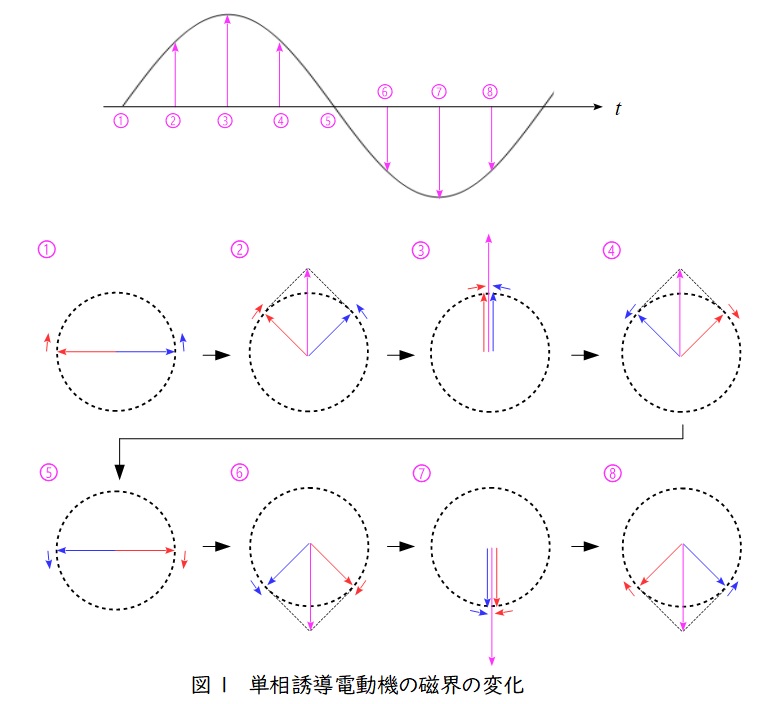
2.単相誘導電動機の磁界の変化
単相誘導電動機は単相の交番磁界により運転する電動機であり，単相の交番磁界は図１のように正方向の回転磁界（青矢印）と逆方向の回転磁界（赤矢印）に分けることができ，２つの回転磁界を合わせたものと考えることができます。
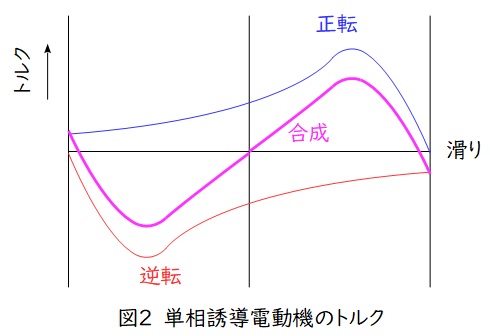
回転磁界によるトルク特性は図２の青矢印と赤矢印で表されるので，その合成トルクは紫矢印のようになり，始動時に回転磁界が発生せず，仮にどちらかに動いた場合にはそちら側にトルクがかかるようになることが分かります。

【解答】

(1)解答：ト
回転磁束\( \ \phi _{\mathrm {f}} \ \)と\( \ \phi _{\mathrm {b}} \ \)は逆向きに回転する磁束なので，
\[
\begin{eqnarray}
\phi _{\mathrm {f}}&=&K\sin \left( \omega _{\mathrm {s}}t+\theta \right) \\[ 5pt ] &=&K\sin \omega _{\mathrm {s}}t\cos \theta +K\cos \omega _{\mathrm {s}}t\sin \theta \\[ 5pt ] \end{eqnarray}
\] とおくと，
\[
\begin{eqnarray}
\phi _{\mathrm {b}} &=& K\sin \left( -\omega _{\mathrm {s}} t+\theta \right) \\[ 5pt ] &=&K\sin \left( -\omega _{\mathrm {s}}t\right) \cos\theta +K\cos \left( -\omega _{\mathrm {s}}t\right) \sin \theta \\[ 5pt ] &=& -K\sin \omega _{\mathrm {s}}t\cos \theta +K\cos \omega _{\mathrm {s}}t\sin \theta \\[ 5pt ] \end{eqnarray}
\] となる。よって，交番磁束は，
\[
\begin{eqnarray}
\phi _{\mathrm {f}}+ \phi _{\mathrm {b}}&=& K\sin \omega _{\mathrm {s}}t\cos \theta +K\cos \omega _{\mathrm {s}}t\sin \theta -K\sin \omega _{\mathrm {s}}t\cos \theta +K\cos \omega _{\mathrm {s}}t\sin \theta \\[ 5pt ] &=& 2K\cos \omega _{\mathrm {s}}t\sin \theta \\[ 5pt ] \end{eqnarray}
\] となるので，それぞれの回転磁束の大きさは交番磁束の最大値の\( \ \displaystyle \frac {1}{2} \ \)倍となる。

(2)解答：ロ
逆方向の回転磁束\( \ \phi _{\mathrm {b}} \ \)に対する滑り\( \ s^{\prime } \ \)は，正方向と同様に考えると，
\[
\begin{eqnarray}
s^{\prime }&=& \frac {-\omega _{\mathrm {s}}-\omega }{-\omega _{\mathrm {s}}} \\[ 5pt ] &=& \frac {\omega _{\mathrm {s}}+\omega }{\omega _{\mathrm {s}}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ル
①より，
\[
\begin{eqnarray}
s&=& \frac {\omega _{\mathrm {s}}-\omega }{\omega _{\mathrm {s}}} \\[ 5pt ] s\omega _{\mathrm {s}}&=& \omega _{\mathrm {s}}-\omega \\[ 5pt ] \omega &=& \left( 1-s \right) \omega _{\mathrm {s}} \\[ 5pt ] \end{eqnarray}
\] となるので，これを②に代入すると，
\[
\begin{eqnarray}
s^{\prime }&=& \frac {\omega _{\mathrm {s}}+\omega }{\omega _{\mathrm {s}}} \\[ 5pt ] &=& \frac {\omega _{\mathrm {s}}+\left( 1-s \right) \omega _{\mathrm {s}} }{\omega _{\mathrm {s}}} \\[ 5pt ] &=&2-s
\end{eqnarray}
\] と求められる。

(4)解答：チ
問題図より，静止時(\( \ s =1 \ \) )の時にはトルクは零となるため，トルクを生じません。

(5)解答：カ
問題図よりわずかに回転させると同方向にトルクがかかるようになり，同期速度(正回転では\( \ s=0 \ \)，逆回転では\( \ s=2 \ \) )まで回転数は上昇します。