《機械》〈照明〉[H26:問6]配光による照明設計に関する空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，配光に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選びなさい。

光源又は照明器具の配光は，照明設計の有力な情報である。それらが照らす空間内の任意の点の照度，任意の方向の光束，照明器具から放射される全光束などを，これによって求めることができる。

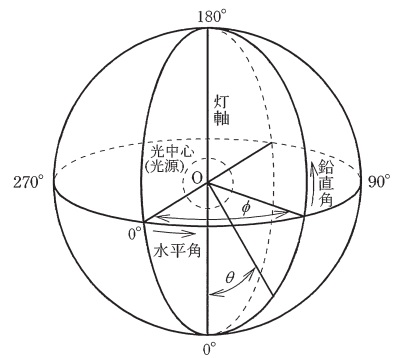
配光は，光源が発散する光束を$ \ \fbox {　（１）　} \ $の空間分布として表したもので，光源を中心とした極座標系(鉛直角$ \ \theta \ $，水平角$ \ \phi \ $ )で表示される。光源が置かれた中心を光中心と呼び，光中心を通る鉛直軸を灯軸という。灯軸を通る断面配光を$ \ \fbox {　（２）　} \ $という。

ある点の照度は，配光によってある点方向の$ \ \fbox {　（１）　} \ $が分かれば，逐点法によって算出することができ，照度は光源からその点までの距離の$ \ \fbox {　（３）　} \ $する。

任意の方向の光束$ \ \mathit {\Phi } \ $は，$ \ \fbox {　（１）　} \ $を$ \ X \ $，立体角を$ \ \omega \ $とすれば，$ \ \mathit {\Phi }=\fbox {　（４）　} \ $である。立体角は，光中心から見たある面に対する空間的広がりの度合いであり，単位はステラジアン(記号：$ \ \mathrm {sr} \ $ )である。光中心から半径$ \ r \ $の球を仮定し，その球表面上のある面積を$ \ S \ $とすれば，その面を切り取る立体角は$ \ \displaystyle \omega =\frac {S}{r^{2}} \ $である。もし，$ \ S \ $が光中心を包囲した閉曲面であれば，立体角は最大の$ \ \fbox {　（５）　} \ \mathrm {sr} \ $になる。

〔問6の解答群〕
\[
\begin{eqnarray}
&（イ）&　鉛直配光　　　　　&（ロ）&　\frac {4}{3}\pi　　　　　&（ハ）&　2乗に反比例 \\[ 5pt ] &（ニ）&　光　度　　　　　&（ホ）&　平方根に比例　　　　　&（ヘ）&　正弦配光 \\[ 5pt ] &（ト）&　逆2乗に反比例　　　　　&（チ）&　照　度　　　　　&（リ）&　X\sqrt {\omega } \\[ 5pt ] &（ヌ）&　輝　度　　　　　&（ル）&　2\pi　　　　　&（ヲ）&　水平配光 \\[ 5pt ] &（ワ）&　4\pi　　　　　&（カ）&　X\cdot \omega　　　　　&（ヨ）&　\frac {X}{\omega } \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

照明に関する問題です。照明は何故か二種では毎年のように出題される一次試験では最重要項目の一つとなっています。出題難易度は低めの問題が多いため，基本公式は確実にマスターしておきましょう。

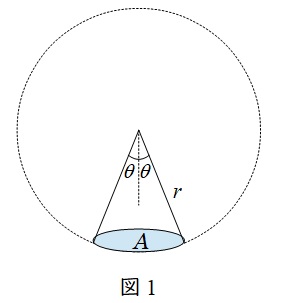
1.立体角$ \ \omega \ $
図1において，$ \ \displaystyle \omega =\frac {A}{r^{2}} \ \mathrm {[sr]} \ $を立体角と言います。
立体角$ \ \omega \ $を角$ \ \theta \ $で表すと，
\[
\omega =2\pi (1-\cos \theta )
\] となり，$ \ \theta =\pi \ $の時，$ \ \omega \ $は最大値$ \ 4\pi \ $となります。

2.光束$ \ \mathit {\Phi } \ $
光の量で単位はルーメン$ \ \mathrm {[lm]} \ $となります。電磁気で言うと磁束のようなものです。

3.光度$ \ I \ $
光束を立体角で割ったものです。微小立体角$ \ \Delta \omega \ $に含まれる光束を$ \ \mathit {\Phi } \ $とすると，光度$ \ I \ $は，
\[
I= \frac {\mathit {\Phi } }{\Delta \omega} \ \mathrm {[cd]}
\] となります。

4.照度$ \ E \ $
均一に照射された面の明るさで，微小面積$ \ \Delta A \ $に入射する光束を$ \ \mathit {\Phi } \ $とすると，
\[
E=\frac {\mathit {\Phi } }{\Delta A}\mathrm {[lx]}
\] となります。

5.配光
光源から各方向への光度の分布を配光と言います。

【解答】

(1)解答：ニ
題意より，解答候補は（ニ）光度，（チ）照度，（ヌ）輝度，になると思いますが，ワンポイント解説「5.配光」の通り，光度となります。

(2)解答：イ
題意より，解答候補は（イ）鉛直配光，（ヘ）正弦配光，（ヲ）水平配光，になると思います。灯軸方向（鉛直方向）の断面配光を鉛直配光と言います。

(3)解答：ハ
題意より，解答候補は（ハ）2乗に反比例，（ホ）平方根に比例，（ト）逆2乗に反比例，となると思います。逆2乗の法則に伴い，照度は距離の2乗に反比例します。

(4)解答：カ
ワンポイント解説「3.光度$I$」の通り，任意の方向の光束$ \ \mathit {\Phi } \ $は，光度を$ \ X \ $，立体角を$ \ \omega \ $とすれば，
\[
\mathit {\Phi }=X\omega
\] となります。

(5)解答：ワ
ワンポイント解説「1.立体角$ \ \omega \ $」の通り，$ \ \theta =\pi \ $の時，
\[
\begin{eqnarray}
\omega &=&2\pi (1-\cos \theta ) \\[ 5pt ] &=&2\pi (1-\cos \pi ) \\[ 5pt ] &=&4\pi \\[ 5pt ] \end{eqnarray}
\] となります。