Contents
【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,誘電加熱に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
誘電加熱は,被加熱物である誘電体を交番電界中に置くことによって誘電体自身が発熱する現象を利用した加熱法である。この発熱は誘電体損と呼ばれている。誘電体に電界が印加されると,誘電体内に\( \ \fbox { (1) } \ \)を生じる。交番電界の場合には,電界の交番に伴って,\( \ \fbox { (1) } \ \)の方向も変化する。交番電界の周波数を上げていくと,交番電界の時間変化に\( \ \fbox { (1) } \ \)が追いつかなくなり,遅れが生じ始める。この遅れによって誘電体損が生じ,その熱によって誘電体自身の温度が上昇する。
誘電体の電気的等価回路は抵抗\( \ R \ \)と静電容量\( \ C \ \)の並列回路で表される。\( \ R \ \)及び\( \ C \ \)を流れる電流をそれぞれ\( \ I_{\mathrm {R}} \ \),\( \ I_{\mathrm {C}} \ \)とすると\( \ \tan \delta = \ \fbox { (2) } \ \)と表され,\( \ \tan \delta \ \)は誘電正接と呼ばれる。また,誘電体の比誘電率を\( \ \varepsilon _{\mathrm {r}} \ \)とすると,\( \ \varepsilon _{\mathrm {r}}\tan \delta \ \)は誘電体の損失係数と呼ばれ,誘電加熱の容易さを判断する目安となる。
誘電損失係数の大きさは印加する交番電界の周波数に大きく依存する。実際の誘電加熱では,放送などの無線業務の障害となるのを避けるため,使用可能な周波数帯が\( \ \fbox { (3) } \ \)周波数帯として定められている。この周波数帯においては,誘電体損を生じる\( \ \fbox { (1) } \ \)は誘電体を構成する荷電体のうち\( \ \fbox { (4) } \ \)によるものである。
また,一般に,被加熱物である誘電体は温度上昇によってインピーダンスが変化するので,誘電加熱装置から被加熱物に電力を効率よく供給するために,高周波発振回路と被加熱物との間に\( \ \fbox { (5) } \ \)が挿入されている。
〔問8の解答群〕
\[
\begin{eqnarray}
&(イ)& 近接効果 &(ロ)& イオン &(ハ)& 移相回路 \\[ 5pt ]
&(ニ)& \mathrm {ISM} &(ホ)& 誘電分極 &(ヘ)& \mathrm {EMS} \\[ 5pt ]
&(ト)& 電子 &(チ)& 整合回路 &(リ)& 渦電流 \\[ 5pt ]
&(ヌ)& \frac {I_{\mathrm {C}}}{I_{\mathrm {R}}} &(ル)& \frac {I_{\mathrm {R}}}{\sqrt {I_{\mathrm {R}}^{2}+I_{\mathrm {C}}^{2}}} &(ヲ)& \frac {I_{\mathrm {R}}}{I_{\mathrm {C}}} \\[ 5pt ]
&(ワ)& \mathrm {EMC} &(カ)& 緩衝回路 &(ヨ)& 電気双極子 \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
誘電加熱の原理やその特徴に関する問題です。
\( \ 3 \ \)種の試験では誘導加熱との比較やその概要程度の出題であったと思いますが,\( \ 2 \ \)種の場合は本問のようにやや深堀りしたような内容が出題されます。
平成29年機械科目問4に類題も出題されていますので,そちらも合わせて見ておくようにして下さい。
1.誘電加熱
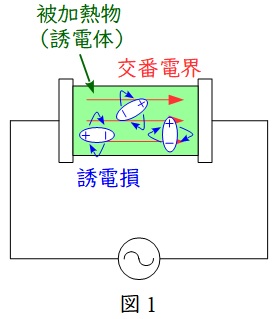
交番電界中に誘電体を置くことによって,誘電体に誘電損が生じ発熱することを利用した加熱方式です。
図1のように平行板電極に被加熱物(誘電体)を挿入し,高周波の電界を加えることで,誘電分極した電気双極子が振動・回転することにより発熱します。電子レンジはこの原理を利用した電化製品の一つです。
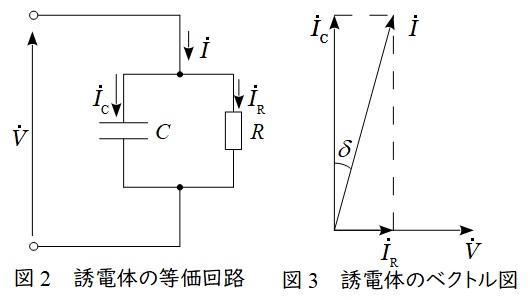
2.誘電正接\( \ \tan \delta \ \)
誘電体の等価回路は図2のように抵抗\( \ R \ \)と静電容量\( \ C \ \)の並列回路となり,コンデンサには図3のようなベクトル図の電流が流れます。この時の\( \ \displaystyle \frac {I_{\mathrm {R}}}{I_{\mathrm {C}}}=\tan \delta \ \)を誘電正接と呼びます。この等価回路における発熱にかかる誘電損\( \ W_{\mathrm {d}} \ \)は,
\[
\begin{eqnarray}
W_{\mathrm {d}}&=&VI_{\mathrm {R}} \\[ 5pt ]
&=&VI_{\mathrm {C}}\tan \delta \\[ 5pt ]
&=&V\omega CV\tan \delta \\[ 5pt ]
&=&\omega CV^{2}\tan \delta \\[ 5pt ]
&=&2\pi f \frac {\varepsilon _{\mathrm {r}}\varepsilon _{\mathrm {0}}S}{d}E^{2}d^{2}\tan \delta \\[ 5pt ]
&=&2\pi fSdE^{2} \varepsilon _{\mathrm {0}}\varepsilon _{\mathrm {r}}\tan \delta \\[ 5pt ]
\end{eqnarray}
\]
となり,発熱量は,電界\( \ E \ \)の\( \ 2 \ \)乗に比例し,周波数\( \ f \ \),比誘電率\( \ \varepsilon _{\mathrm {r}} \ \),誘電正接\( \ \tan \delta \ \)に比例することがわかります。\( \ \varepsilon _{\mathrm {r}}\tan \delta \ \)を損失係数といいます。
【解答】
(1)解答:ホ
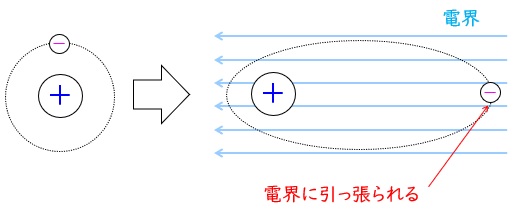
題意より解答候補は,(イ)近接効果,(ロ)イオン,(ホ)誘電分極,(ト)電子,(リ)渦電流,(ヨ)電気双極子,等になると思います。
ワンポイント解説「1.誘電加熱」の通り,誘電体に電界を加えることで電子が電界に引っ張られプラスとマイナスの電気双極子ができることを誘電分極といいます。
(2)解答:ヲ
題意より解答候補は,(ヌ)\( \ \displaystyle \frac {I_{\mathrm {C}}}{I_{\mathrm {R}}} \ \),(ル)\( \ \displaystyle \frac {I_{\mathrm {R}}}{\sqrt {I_{\mathrm {R}}^{2}+I_{\mathrm {C}}^{2}}} \ \),(ヲ)\( \ \displaystyle \frac {I_{\mathrm {R}}}{I_{\mathrm {C}}} \ \),になると思います。
ワンポイント解説「2.誘電正接\( \ \tan \delta \ \)」の通り,\( \ \tan \delta = \displaystyle \frac {I_{\mathrm {R}}}{I_{\mathrm {C}}} \)となります。
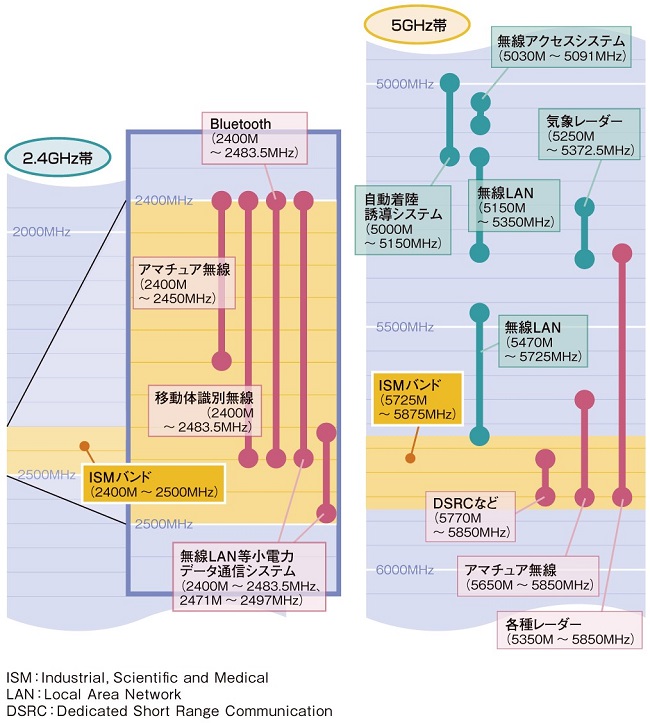
(3)解答:ニ
題意より解答候補は,(ニ)\( \ \mathrm {ISM} \ \),(ヘ)\( \ \mathrm {EMS} \ \),(ワ)\( \ \mathrm {EMC} \ \),になると思います。
放送などの無線業務の障害となるのを避けるために割り当てられた周波数の帯を\( \ \mathrm {ISM} \ \)周波数帯と言います。
出典:日経クロステック ISMバンド 2010,09.22 記事
(4)解答:ヨ
題意より解答候補は,(イ)近接効果,(ロ)イオン,(ホ)誘電分極,(ト)電子,(リ)渦電流,(ヨ)電気双極子,等になると思います。
ワンポイント解説「1.誘電加熱」の通り,誘電体損を生じる誘電分極は電気双極子によるものとなります。
(5)解答:チ
題意より解答候補は,(ハ)移相回路,(チ)整合回路,(カ)緩衝回路,等になると思います。
誘電加熱装置から被加熱物に電力を効率よく供給するために,高周波発振回路と被加熱物との間に挿入する回路を整合回路と言います。こちらは回路構成等の知識は不要ですので,名称だけ覚えておいて下さい。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは