Contents
【問題】
【難易度】★★★☆☆(普通)
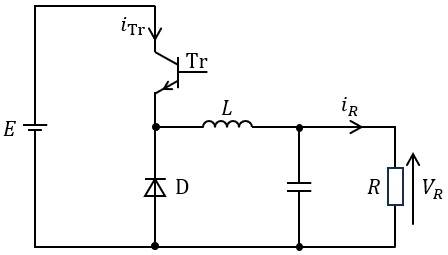
図のような降圧チョッパ回路において,周囲温度は\( \ 40 \ \mathrm {[{}^{\circ }C]} \ \),抵抗負荷\( \ R \ \)に一定の直流電圧\( \ 120 \ \mathrm {[V]} \ \)で直流電流\( \ 50 \ \mathrm {[A]} \ \)が供給されているとする。
このときの運転条件において,トランジスタ\( \ \mathrm {Tr} \ \)のオン電圧は\( \ 3 \ \mathrm {[V]} \ \),ダイオード\( \ \mathrm {D} \ \)のオン電圧は\( \ 1 \ \mathrm {[V]} \ \)であった。トランジスタ\( \ \mathrm {Tr} \ \)とダイオード\( \ \mathrm {D} \ \)のスイッチング損失は無視できるものとし,リアクトル\( \ L \ \)に流れる電流は一定で,その損失は無視できるものとする。また,トランジスタ\( \ \mathrm {Tr} \ \)が導通する比率\( \ \displaystyle \left( \frac {オン期間}{オン期間+オフ期間} \right) \ \)は\( \ 60 \ \mathrm {[%]} \ \),ヒートシンクを含めたトランジスタ\( \ \mathrm {Tr} \ \)のジャンクションー周囲空気の間の熱抵抗は\( \ 0.5 \ \mathrm {[{}^{\circ }C / W]} \ \)とし,放射などの他の熱放散は無視できるものとする。
この装置においてはトランジスタ\( \ \mathrm {Tr} \ \)のジャンクション温度が装置の使用条件を制限しているので,この装置を高い周囲温度\( \ \left( 50 \ \mathrm {[{}^{\circ }C]} \right) \ \)で使うために,装置の冷却風を強化して熱抵抗の改善を検討する。トランジスタ\( \ \mathrm {Tr} \ \)とダイオード\( \ \mathrm {D} \ \)の使用温度に依存するオン電圧の特性変化は無視できるものとして,次の問に答えよ。
(1) 一般的に,パワーデバイスの損失\( \ P \ \mathrm {[W]} \ \),ジャンクションー周囲空気の間の熱抵抗\( \ R_{th} \ \mathrm {[{}^{\circ }C / W]} \ \)及び周囲温度\( \ T_{a} \ \mathrm {[{}^{\circ }C]} \ \)とするとき,使用しているパワーデバイスのジャンクション温度\( \ T_{j} \ \mathrm {[{}^{\circ }C]} \ \)はどのように表されるか。ただし,他のパワーデバイスとの温度干渉はないものとする。
(2) 周囲温度\( \ 40 \ \mathrm {[{}^{\circ }C]} \ \)のとき,トランジスタ\( \ \mathrm {Tr} \ \)のオン損失\( \ W_{CON(\mathrm {Tr})} \ \mathrm {[W]} \ \)の値はいくらになるか。
(3) 周囲温度\( \ 40 \ \mathrm {[{}^{\circ }C]} \ \)のとき,トランジスタ\( \ \mathrm {Tr} \ \)のジャンクション温度\( \ T_{j(\mathrm {Tr})} \ \mathrm {[{}^{\circ }C]} \ \)の値はいくらになるか。
(4) 周囲温度\( \ 50 \ \mathrm {[{}^{\circ }C]} \ \)で,周囲温度\( \ 40 \ \mathrm {[{}^{\circ }C]} \ \)のときと同じジャンクション温度で使用するためには,トランジスタ\( \ \mathrm {Tr} \ \)のジャンクションー周囲空気の間の熱抵抗を何%までに低減するようにしなければならないか。
【ワンポイント解説】
降圧チョッパのトランジスタでの損失による周囲温度の上昇に関する問題です。
内容自体はそれほど難解ではありませんが,あまり熱力学と組み合わせたような問題は電験では出題されてこなかったので,初見の受験生には厳しい問題であったかもしれません。機械科目で出題される電熱の内容を理解しておくようにしましょう。
1.降圧チョッパの動作
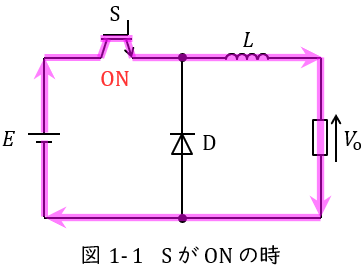
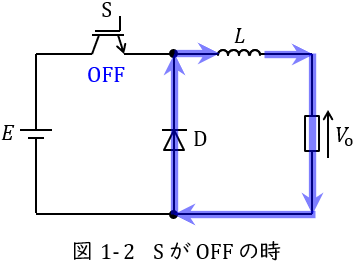
図1-1及び図1-2は降圧チョッパの例となります。
スイッチ\( \ \mathrm {S} \ \)がオンになると,図1-1のように電源からの電流はスイッチ\( \ \mathrm {S} \ \)を通り,リアクトル\( \ L \ \)側に電流が流れますが,ダイオード\( \ D_{\mathrm {F}} \ \)は逆向きなので電流が流れません。
スイッチ\( \ \mathrm {S} \ \)がオフになると,図1-2のように電源から電流は流れず,リアクトルに蓄えられているエネルギーから出力側と還流ダイオード\( \ D_{\mathrm {F}} \ \)に電流が流れます。
したがって,降圧チョッパの出力電圧の平均値\( \ V_{\mathrm {out}} \ \)は,スイッチのオン時間を\( \ T_{\mathrm {on}} \ \),オフ時間を\( \ T_{\mathrm {off}} \ \)とすると,
\[
\begin{eqnarray}
V_{\mathrm {out}}&=&\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}V_{\mathrm {in}} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。このとき,\( \ V_{\mathrm {in}} \ \)の係数
\[
\begin{eqnarray}
\gamma &=&\frac {T_{\mathrm {ON}}}{T_{\mathrm {ON}}+T_{\mathrm {OFF}}} \\[ 5pt ]
\end{eqnarray}
\]
を通流率といいます。
2.熱力学におけるオームの法則
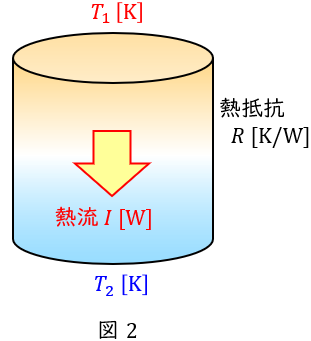
図2に示すように,ある温度差がある物体においては高温部から低温部に向かい熱が伝わり,それを熱流といいます。
物体の温度差を\( \ \theta =T_{1}-T_{2} \ \mathrm {[K]} \ \),熱抵抗を\( \ R \ \mathrm {[K / W]} \ \)とすると,物体の熱流\( \ I \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
I &=& \frac {\theta }{R} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)使用しているパワーデバイスのジャンクション温度\( \ T_{j} \ \mathrm {[{}^{\circ }C]} \ \)の式
ワンポイント解説「2.熱力学におけるオームの法則」の通り,
\[
\begin{eqnarray}
P &=& \frac {T_{j}- T_{a}}{R_{th}} \\[ 5pt ]
T_{j}- T_{a}&=& PR_{th} \\[ 5pt ]
T_{j}&=&PR_{th}+T_{a} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)周囲温度\( \ 40 \ \mathrm {[{}^{\circ }C]} \ \)のとき,トランジスタ\( \ \mathrm {Tr} \ \)のオン損失\( \ W_{CON(\mathrm {Tr})} \ \mathrm {[W]} \ \)
題意より,トランジスタ\( \ \mathrm {Tr} \ \)のオン電圧\( \ V_{CE}=3 \ \mathrm {[V]} \ \),負荷\( \ R \ \)の直流電流\( \ i_{R}=50 \ \mathrm {[A]} \ \),トランジスタ\( \ \mathrm {Tr} \ \)の通流率\( \ \gamma =0.6 \ \)であり,トランジスタ\( \ \mathrm {Tr} \ \)にはオンのときのみ電流が流れるので,オン損失\( \ W_{CON(\mathrm {Tr})} \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
W_{CON(\mathrm {Tr})} &=& V_{CE}\cdot \gamma i_{R} \\[ 5pt ]
&=& 3\times 0.6\times 50 \\[ 5pt ]
&=& 90 \ \mathrm {[W]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)周囲温度\( \ 40 \ \mathrm {[{}^{\circ }C]} \ \)のとき, トランジスタ\( \ \mathrm {Tr} \ \)のジャンクション温度\( \ T_{j(\mathrm {Tr})} \ \mathrm {[{}^{\circ }C]} \ \)
題意より,トランジスタ\( \ \mathrm {Tr} \ \)のスイッチング損失は無視できるので,トランジスタ\( \ \mathrm {Tr} \ \)の損失は\( \ W_{CON(\mathrm {Tr})}=90 \ \mathrm {[W]} \ \)のみと考えればよい。したがって,(1)解答式よりトランジスタ\( \ \mathrm {Tr} \ \)のジャンクション温度\( \ T_{j(\mathrm {Tr})} \ \mathrm {[{}^{\circ }C]} \ \)は,
\[
\begin{eqnarray}
T_{j(\mathrm {Tr})}&=&W_{CON(\mathrm {Tr})}R_{th}+T_{a(\mathrm {Tr})} \\[ 5pt ]
&=&90\times 0.5+40 \\[ 5pt ]
&=&85 \ \mathrm {[{}^{\circ }C]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)周囲温度\( \ 50 \ \mathrm {[{}^{\circ }C]} \ \)のときのトランジスタ\( \ \mathrm {Tr} \ \)のジャンクションー周囲空気の間の熱抵抗
\( \ {T_{a(\mathrm {Tr})}}^{\prime }=50 \ \mathrm {[{}^{\circ }C]} \ \)における熱抵抗\( \ {R_{th}}^{\prime } \ \mathrm {[{}^{\circ }C / W]} \ \)は,
\[
\begin{eqnarray}
T_{j(\mathrm {Tr})}&=&W_{CON(\mathrm {Tr})}{R_{th}}^{\prime }+{T_{a(\mathrm {Tr})}}^{\prime } \\[ 5pt ]
85&=&90{R_{th}}^{\prime }+50 \\[ 5pt ]
90{R_{th}}^{\prime }&=&35 \\[ 5pt ]
{R_{th}}^{\prime }&≒&0.388 \ 88 \ \mathrm {[{}^{\circ }C / W]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,低減率\( \ \alpha \ \mathrm {[%]} \ \)は,
\[
\begin{eqnarray}
\alpha &=&\frac {{R_{th}}^{\prime }}{R_{th}}\times 100 \\[ 5pt ]
&=&\frac {0.388 \ 88}{0.5}\times 100 \\[ 5pt ]
&≒&77.8 \ \mathrm {[%]}
\end{eqnarray}
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは