《機械・制御》〈変圧器〉[R03:問2]変圧器の短絡試験結果からの各値の導出に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

容量\( \ 200 \ \mathrm {kV\cdot A} \ \)，一次電圧\( \ 11 \ 000 \ \mathrm {V} \ \)，二次電圧\( \ 440 \ \mathrm {V} \ \)，周波数\( \ 50 \ \mathrm {Hz} \ \)を定格とし，自己容量基準の短絡インピーダンス\( \ ％z \ \)が\( \ 4.5 \ \mathrm {％} \ \)の単相変圧器がある。この変圧器の二次側を短絡し一次側に定格電流を流したときの一次側の電力計の指示は\( \ 1.5 \ \mathrm {kW} \ \)であった。

この変圧器について，次の問に答えよ。ただし，変圧器の励磁電流，鉄損は無視できるものとする。

(1)　\( \ ％z \ \)のうち抵抗分\( \ \left( ％r\right) \ \)，リアクタンス分\( \ \left( ％x\right) \ \)を答えよ。

(2)　短絡インピーダンスの一次換算値\( \ Z \ \mathrm {[\Omega ]} \ \)を答えよ。

(3)　\( \ Z \ \mathrm {[\Omega ]} \ \)の抵抗分\( \ R \ \mathrm {[\Omega ]} \ \)及び，リアクタンス分\( \ X \ \mathrm {[\Omega ]} \ \)を答えよ。

(4)　この変圧器の二次側にリアクトルを接続し，一次側に交流\( \ 11 \ 000 \ \mathrm {V} \ \)を加えたときの二次電流は\( \ 400 \ \mathrm {A} \ \)であった。このときの変圧器二次電圧\( \ V_{2} \ \mathrm {[V]} \ \)及び，リアクトルの無効電力\( \ Q_{\mathrm {L}} \ \mathrm {[kvar]} \ \)を求めよ。なお，リアクトルの抵抗分は無視してよい。

【ワンポイント解説】

変圧器の短絡試験から変圧器の抵抗分及びリアクタンス分を求め，さらに二次側にリアクトルを接続したときの電圧の導出を行う問題です。
(1)\( \ ％r \ \)の導出さえできれば(1)～(3)は比較的易しい問題ですが，(4)が考え方を理解できるかどうかで解けるか解けないか分かれる問題です。
(1)～(3)を解いておけば十分に合格圏内に到達できると考えられるので，試験本番でも無理せず確実に得点できるところを得点するようにしましょう。

1.変圧器の等価回路（一次換算）
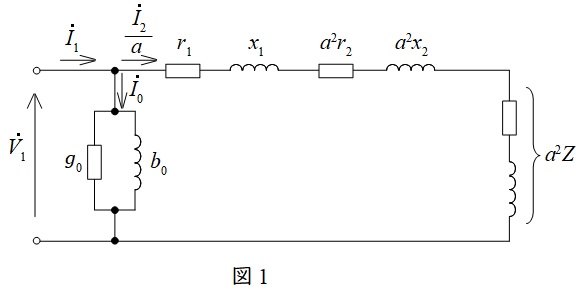
変圧器の一次換算等価回路を図1に示します。ただし，\( \ {\dot V}_{1} \ \)は一次側端子電圧，\( \ {\dot I}_{1} \ \)は一次電流，\( \ {\dot I}_{2} \ \)は二次電流，\( \ {\dot I}_{0} \ \)は励磁電流，\( \ r_{1} \ \)は一次巻線抵抗，\( \ r_{2} \ \)は二次巻線抵抗，\( \ x_{1} \ \)は一次漏れリアクタンス，\( \ x_{2} \ \)は二次漏れリアクタンス，\( \ a \ \)は変圧比（巻数比）となります。

2.無負荷試験の等価回路
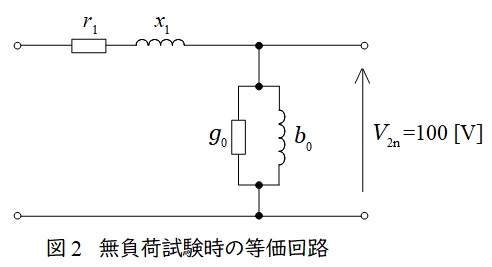
変圧器の無負荷試験は一次側を開放して，二次側に定格電圧を加える試験です。測定される電力は鉄損となり，測定される電力と電流から，励磁コンダクタンス\( \ g_{0} \ \)及び励磁サセプタンス\( \ b_{0} \ \)を求めることが可能となります。二次側に定格電圧を加えるのが一般的ですが，二次側開放で一次側に定格電圧を加えても同様に求められます。

3.短絡試験の等価回路
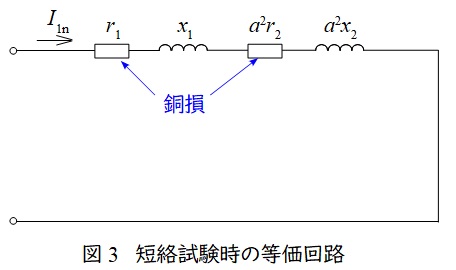
変圧器の短絡試験は二次側を短絡して，一次側にインピーダンス電圧を加えて，定格電流を流す試験です。励磁回路に流れる電流が十分に小さいと仮定すると，測定される電力は銅損となります。測定される電力と電流から，高圧側換算の巻線抵抗\( \ R=r_{1}+a^{2}r_{2} \ \)を求めることが可能となります

4.オーム法からパーセントインピーダンス法への変換（単相回路）
基準容量を\( \ P_{\mathrm {n}} \ \)，基準電圧を\( \ V_{\mathrm {n}} \ \)，基準電流を\( \ I_{\mathrm {n}} \ \)とすると，
\[
\begin{eqnarray}
％Z&=&\frac {ZI_{\mathrm {n}}}{V_{\mathrm {n}}}\times 100　　 (定義) \\[ 5pt ] &=&\frac {ZV_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}}\times 100 \\[ 5pt ] &=&\frac {P_{\mathrm {n}}Z}{V_{\mathrm {n}}^{2}}\times 100　　 (∵P_{\mathrm {n}}=V_{\mathrm {n}}I_{\mathrm {n}} ) \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)\( \ ％z \ \)のうち抵抗分\( \ \left( ％r\right) \ \)，リアクタンス分\( \ \left( ％x\right) \ \)
ワンポイント解説「4.オーム法からパーセントインピーダンス法への変換（単相回路）」の百分率インピーダンスの定義式から，
\[
\begin{eqnarray}
％r&=&\frac {RI_{\mathrm {1n}}}{V_{\mathrm {1n}}}\times 100 \\[ 5pt ] &=&\frac {RI_{\mathrm {1n}}^{2}}{V_{\mathrm {1n}}I_{\mathrm {1n}}}\times 100 \\[ 5pt ] &=&\frac {RI_{\mathrm {1n}}^{2}}{P_{\mathrm {n}}}\times 100 \\[ 5pt ] \end{eqnarray}
\] と変形できる。短絡試験を実施したときの一次側の電力計の指示が\( \ 1.5 \ \mathrm {kW} \ \)であり，これは抵抗で消費される電力\( \ RI_{\mathrm {1n}}^{2} \ \)と等しいので，
\[
\begin{eqnarray}
％r&=&\frac {RI_{\mathrm {1n}}^{2}}{P_{\mathrm {n}}}\times 100 \\[ 5pt ] &=&\frac {1.5\times 10^{3}}{200\times 10^{3}}\times 100 \\[ 5pt ] &=&0.75 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。また，\( \ ％z=\sqrt {％r^{2}+％x^{2}} \ \)より，
\[
\begin{eqnarray}
％x&=&\sqrt {％z^{2}-％r^{2}} \\[ 5pt ] &=&\sqrt {4.5^{2}-0.75^{2}} \\[ 5pt ] &≒&4.4371　→　4.44 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)短絡インピーダンスの一次換算値\( \ Z \ \mathrm {[\Omega ]} \ \)
ワンポイント解説「4.オーム法からパーセントインピーダンス法への変換（単相回路）」の通り，
\[
\begin{eqnarray}
％Z&=&\frac {P_{\mathrm {n}}Z}{V_{\mathrm {1n}}^{2}}\times 100 \\[ 5pt ] Z&=&\frac {％ZV_{\mathrm {1n}}^{2}}{100P_{\mathrm {n}}} \\[ 5pt ] &=&\frac {4.5\times 11 \ 000^{2}}{100\times 200\times 10^{3}} \\[ 5pt ] &=&27.225　→　27.2 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)\( \ Z \ \mathrm {[\Omega ]} \ \)の抵抗分\( \ R \ \mathrm {[\Omega ]} \ \)及び，リアクタンス分\( \ X \ \mathrm {[\Omega ]} \ \)
(2)と同様に抵抗分とリアクタンス分も求めると，
\[
\begin{eqnarray}
％r&=&\frac {P_{\mathrm {n}}R}{V_{\mathrm {1n}}^{2}}\times 100 \\[ 5pt ] R&=&\frac {％rV_{\mathrm {1n}}^{2}}{100P_{\mathrm {n}}} \\[ 5pt ] &=&\frac {0.75\times 11 \ 000^{2}}{100\times 200\times 10^{3}} \\[ 5pt ] &=&4.5375　→　4.54 \ \mathrm {[\Omega ]} \\[ 5pt ] ％x&=&\frac {P_{\mathrm {n}}X}{V_{\mathrm {1n}}^{2}}\times 100 \\[ 5pt ] X&=&\frac {％xV_{\mathrm {1n}}^{2}}{100P_{\mathrm {n}}} \\[ 5pt ] &=&\frac {4.4371\times 11 \ 000^{2}}{100\times 200\times 10^{3}} \\[ 5pt ] &=&26.844　→　26.8 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)題意の条件における変圧器二次電圧\( \ V_{2} \ \mathrm {[V]} \ \)及び，リアクトルの無効電力\( \ Q_{\mathrm {L}} \ \mathrm {[kvar]} \ \)
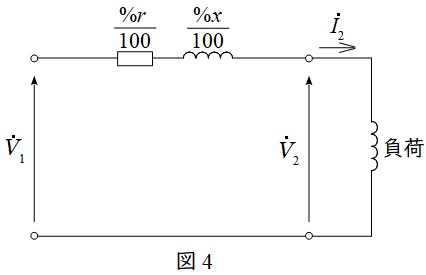
二次側にリアクトルを接続したときの等価回路を図4に示す。二次定格電流\( \ I_{\mathrm {2n}} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {2n}}&=&\frac {P_{\mathrm {n}}}{V_{\mathrm {2n}}} \\[ 5pt ] &=&\frac {200\times 10^{3}}{440} \\[ 5pt ] &≒&454.545 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] であり，二次側にリアクトルを接続したときの二次電流\( \ I_{2}=400 \ \mathrm {[A]} \ \)であるから，その百分率インピーダンス値\( \ ％I_{2} \ \mathrm {[％]} \ \)は，
\[
\begin{eqnarray}
％I_{\mathrm {2}}&=&\frac {I_{\mathrm {2}}}{I_{\mathrm {2n}}}\times 100 \\[ 5pt ] &=&\frac {400}{454.545}\times 100 \\[ 5pt ] &≒&88.000 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
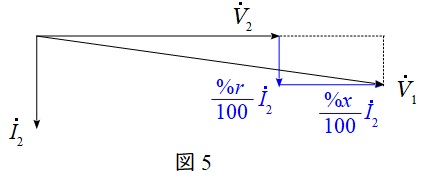
\] となる。したがって，単位法におけるベクトル図は図5のように描けるので，三平方の定理を適用すると，
\[
\begin{eqnarray}
\left( \frac {％V_{1}}{100}\right) ^{2}&=&\left(\frac {％V_{2}}{100}+\frac {％x}{100}\cdot \frac {％I_{2}}{100}\right) ^{2}+\left( \frac {％r}{100}\cdot \frac {％I_{2}}{100}\right) ^{2} \\[ 5pt ] \left( \frac {％V_{2}}{100}+\frac {％x}{100}\cdot \frac {％I_{2}}{100}\right) ^{2}&=&\left( \frac {％V_{1}}{100}\right) ^{2}-\left( \frac {％r}{100}\cdot \frac {％I_{2}}{100}\right) ^{2} \\[ 5pt ] \frac {％V_{2}}{100}+\frac {％x}{100}\cdot \frac {％I_{2}}{100}&=&\sqrt {\left( \frac {％V_{1}}{100}\right) ^{2}-\left( \frac {％r}{100}\cdot \frac {％I_{2}}{100}\right) ^{2}} \\[ 5pt ] \frac {％V_{2}}{100}&=&\sqrt {\left( \frac {％V_{1}}{100}\right) ^{2}-\left( \frac {％r}{100}\cdot \frac {％I_{2}}{100}\right) ^{2}}-\frac {％x}{100}\cdot \frac {％I_{2}}{100} \\[ 5pt ] &=&\sqrt {\left( \frac {100}{100}\right) ^{2}-\left( \frac {0.75}{100}\times \frac {88}{100} \right) ^{2}}-\frac {4.4371}{100}\times \frac {88}{100} \\[ 5pt ] &≒&0.96093 \\[ 5pt ] ％V_{2}&=&0.96093\times 100 \\[ 5pt ] &=&96.093 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] となるので，二次電圧\( \ V_{2} \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
％V_{2}&=&\frac {V_{2}}{V_{\mathrm {2n}}}\times 100 \\[ 5pt ] V_{2}&=&\frac {％V_{2}}{100}V_{\mathrm {2n}} \\[ 5pt ] &=&\frac {96.093}{100}\times 440 \\[ 5pt ] &≒&422.81　→　423 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。また，リアクトルの無効電力\( \ Q_{\mathrm {L}} \ \mathrm {[kvar]} \ \)は，
\[
\begin{eqnarray}
Q_{\mathrm {L}}&=&V_{2}I_{2} \\[ 5pt ] &=&422.81\times 400 \\[ 5pt ] &≒&169120 \ \mathrm {[var]}　→　169 \ \mathrm {[kvar]} \\[ 5pt ] \end{eqnarray}
\] と求められる。