Contents
【問題】
【難易度】★★★★☆(やや難しい)
図に示すフィードバック制御系について,次の問に答えよ。ただし,\( \ R \left( s\right) \ \)は目標値,\( \ U \left( s\right) \ \)は操作量,\( \ Y \left( s\right) \ \)は出力,\( \ E \left( s\right) \ \)は偏差であり,時間信号\( \ r \left( t\right) \ \),\( \ u \left( t\right) \ \),\( \ y \left( t\right) \ \),\( \ e \left( t\right) \ \)をそれぞれラプラス変換したものである。
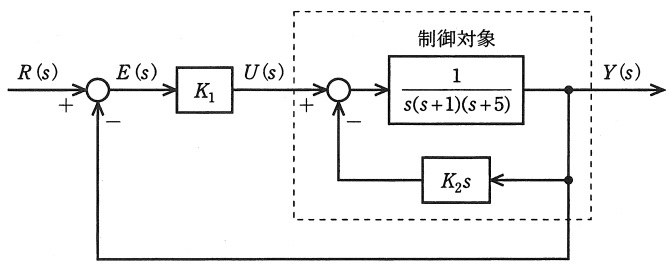
(1) 点線で囲まれたブロック線図だけを取り出したとき,\( \ U \left( s\right) \ \)から\( \ Y \left( s\right) \ \)までの伝達関数を求めよ。
(2) \( \ R \left( s\right) \ \)から\( \ Y \left( s\right) \ \)までの伝達関数を求めよ。
(3) 図のフィードバック制御系が安定となるための\( \ K_{1} \ \)と\( \ K_{2} \ \)が満たすべき条件及び安定限界における持続振動の角周波数\( \ \omega _{c} \ \)を\( \ K_{2} \ \)を用いて表せ。
(4) 目標値\( \ r \left( t\right) \ \)がランプ関数\( \ r \left( t\right) =t \ \)のときの定常速度偏差を求めよ。
(5) 図のフィードバック制御系が安定となるように\( \ K_{1} \ \)と\( \ K_{2} \ \)が選ばれるとする。上記(3)及び(4)の結果を踏まえて,以下の問に答えよ。
a.\( \ K_{1} \ \)を固定したとき,\( \ K_{2} \ \)を大きくすると,速応性と定常特性はどのように変化するかを理由とともに答えよ。
b.\( \ K_{2} \ \)を固定したとき,\( \ K_{1} \ \)を大きくすると,減衰特性と定常特性はどのように変化するかを理由とともに答えよ。
【ワンポイント解説】
フィードバック制御系の伝達関数と安定判別,定常特性に関する問題です。
伝達関数を3回演算しなければならず,安定判別も必要となるため,時間的にはタイトとなる問題と言えます。
いずれも自動制御としては重要な内容を多く含むため,ぜひ理解するようにしましょう。
1.基本的なラプラス変換
\( \ f(t) \ \)のラプラス変換を\( \ F(s) \ \)とすると以下のような関係があります。
\[
\begin{array}{|c|c|}
\hline
f(t) & F(s) \\
\hline
{\displaystyle \delta (t) }\atop{単位インパルス関数} & 1 \\[ 5pt ]
{\displaystyle u (t) }\atop{単位ステップ関数} & \displaystyle \frac {1}{s} \\[ 5pt ]
K & \displaystyle \frac {K}{s} \\[ 5pt ]
t & \displaystyle \frac {1}{s^{2}} \\[ 5pt ]
\mathrm {e}^{at} & \displaystyle \frac {1}{s-a} \\[ 5pt ]
\sin \omega t & \displaystyle \frac {\omega }{s^{2}+\omega ^{2}} \\[ 5pt ]
\cos \omega t & \displaystyle \frac {s}{s^{2}+\omega ^{2}} \\[ 5pt ]
\displaystyle \frac {\mathrm {d}f\left( t \right) }{\mathrm {d}t} & sF\left( s \right) -f\left( 0 \right) \\[ 5pt ]
\displaystyle \int f\left( t \right) \mathrm {d}t & \displaystyle \frac {F\left( s \right) }{s}+\frac {1}{s}\int _{-\infty }^{0}f\left( \tau \right) \mathrm {d}\tau \\[ 5pt ]
\hline
\end{array}
\]
2.ブロック線図の考え方
①直列
図1のような伝達関数\( \ G_{1}(s) \ \),\( \ G_{2}(s) \ \)が与えられているとき,全体の伝達関数\( \ G(s) \ \)は,
\[
\begin{eqnarray}
G(s)&=&\frac {Y(s)}{X(s)}=G_{1}(s)G_{2}(s) \\[ 5pt ]
\end{eqnarray}
\]
となります。
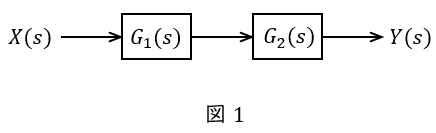
②並列
図2のような伝達関数\( \ G_{1}(s) \ \),\( \ G_{2}(s) \ \)が与えられているとき,全体の伝達関数\( \ G(s) \ \)は,
\[
\begin{eqnarray}
G(s)&=&\frac {Y(s)}{X(s)}=G_{1}(s)±G_{2}(s) \\[ 5pt ]
\end{eqnarray}
\]
となります。
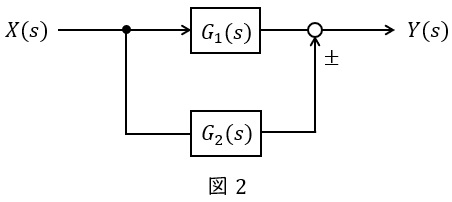
③フィードバック
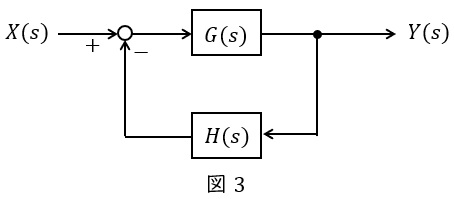
図3のような\( \ G(s) \ \),\( \ H(s) \ \)が与えられているとき,全体の伝達関数\( \ W(s) \ \)は,
\[
\begin{eqnarray}
Y(s)&=&\left\{ X(s) -H(s)Y(s) \right\} G(s) \\[ 5pt ]
Y(s)&=&G(s)X(s) -G(s)H(s)Y(s) \\[ 5pt ]
Y(s)+G(s)H(s)Y(s) &=&G(s)X(s) \\[ 5pt ]
\left\{ 1+G(s)H(s)\right\} Y(s) &=&G(s)X(s) \\[ 5pt ]
\frac {Y(s)}{X(s)}&=&\frac {G(s)}{1+G(s)H(s)} \\[ 5pt ]
W(s)&=&\frac {G(s)}{1+G(s)H(s)} \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.ラウスの安定判別法
特性方程式\( \ a_{0}s^{n}+a_{1}s^{n-1}+a_{2}s^{n-2}+\cdots +a_{n-1}s+a_{n}=0 \ \)が与えられている時,ラウスの安定判別法による安定条件は,
\[
\begin{eqnarray}
&&1. s^{n},s^{n-1},\cdots ,s^{1},s^{0}の係数がすべて存在 \\[ 5pt ]
&&2. s^{n},s^{n-1},\cdots ,s^{1},s^{0}の係数がすべて同符号 \\[ 5pt ]
&&3. ラウスの数表の値がすべて正であること \\[ 5pt ]
\end{eqnarray}
\]
です。ラウスの数表は下図のようになります。
\[
\begin{array}{c|ccc}
& 1列 & 2列 & 3列 \\
\hline
1行 & a_{0} & a_{2} & a_{4} & \cdots \\
2行 & a_{1} & a_{3} & a_{5} & \cdots \\
3行 & b_{1}=\frac {a_{1}a_{2}-a_{0}a_{3}}{a_{1}} & b_{2}=\frac {a_{1}a_{4}-a_{0}a_{5}}{a_{1}} & \cdots \\
4行 & c_{1}=\frac {b_{1}a_{3}-a_{1}b_{2}}{b_{1}} & c_{2}=\frac {b_{1}a_{5}-a_{1}b_{3}}{b_{1}} & \cdots \\
\vdots & \vdots & \vdots &
\end{array}
\]
4.最終値の定理
\( \ f(t) \ \)のラプラス変換を\( \ F(s) \ \)とすると,\( \ f(t) \ \)の定常値は,
\[
\begin{eqnarray}
\displaystyle \lim _{ t \to \infty } f(t)&=&\displaystyle \lim _{ s \to 0 } sF(s) \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
【解答】
(1)\( \ U \left( s\right) \ \)から\( \ Y \left( s\right) \ \)までの伝達関数
点線内のブロック線図において,
\[
\begin{eqnarray}
\left\{ U\left( s \right) -K_{2}sY\left( s \right) \right\} \frac {1}{s\left( s+1\right) \left( s+5\right) }&=&Y\left( s \right) \\[ 5pt ]
\end{eqnarray}
\]
の関係があるから,これを整理すると,
\[
\begin{eqnarray}
U\left( s \right) -K_{2}sY\left( s \right) &=&Y\left( s \right) \left\{ s\left( s+1\right) \left( s+5\right) \right\} \\[ 5pt ]
&=&Y\left( s \right) \left( s^{3}+6s^{2}+5s \right) \\[ 5pt ]
U\left( s \right) &=&Y\left( s \right) \left( s^{3}+6s^{2}+5s \right) +K_{2}sY\left( s \right) \\[ 5pt ]
&=&Y\left( s \right) \left\{ s^{3}+6s^{2}+\left( K_{2}+5\right) s \right\} \\[ 5pt ]
\frac {Y\left( s \right) }{U\left( s \right) }&=&\frac {1}{s^{3}+6s^{2}+\left( K_{2}+5\right) s } \\[ 5pt ]
&=&\frac {1}{s\left( s^{2}+6s+ K_{2}+5\right) } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)\( \ R \left( s\right) \ \)から\( \ Y \left( s\right) \ \)までの伝達関数
(1)で求めた伝達関数を\( \ W \left( s\right) \ \)とおくと,問題図のブロック線図における関係式は,
\[
\begin{eqnarray}
\left\{ R\left( s \right) -Y\left( s \right) \right\} K_{1}\cdot W\left( s \right) &=&Y\left( s \right) \\[ 5pt ]
\end{eqnarray}
\]
となるので,これを整理し計算していくと,
\[
\begin{eqnarray}
K_{1}W\left( s \right) R\left( s \right) -K_{1}W\left( s \right) Y\left( s \right) &=&Y\left( s \right) \\[ 5pt ]
K_{1}W\left( s \right) R\left( s \right) &=&Y\left( s \right) +K_{1}W\left( s \right) Y\left( s \right) \\[ 5pt ]
&=&\left\{ 1+K_{1}W\left( s \right) \right\} Y\left( s \right) \\[ 5pt ]
\frac {Y\left( s \right)}{R\left( s \right) } &=&\frac {K_{1}W\left( s \right) }{1 +K_{1}W\left( s \right) } \\[ 5pt ]
&=&\frac {K_{1}\cdot \displaystyle \frac {1}{s\left( s^{2}+6s+ K_{2}+5\right) }}{1 +K_{1}\cdot \displaystyle \frac {1}{s\left( s^{2}+6s+ K_{2}+5\right) }} \\[ 5pt ]
&=&\frac {\displaystyle \frac {K_{1}}{s\left( s^{2}+6s+ K_{2}+5\right) }}{\displaystyle \frac {s\left( s^{2}+6s+ K_{2}+5\right) +K_{1}}{s\left( s^{2}+6s+ K_{2}+5\right) }} \\[ 5pt ]
&=&\frac {K_{1}}{s\left( s^{2}+6s+ K_{2}+5\right) +K_{1}} \\[ 5pt ]
&=&\frac {K_{1}}{s^{3}+6s^{2}+ \left( K_{2}+5\right) s+K_{1}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)フィードバック制御系が安定となるための\( \ K_{1} \ \)と\( \ K_{2} \ \)が満たすべき条件及び安定限界における持続振動の角周波数
(2)解答式において,特性方程式は\( \ s^{3}+6s^{2}+ \left( K_{2}+5\right) s+K_{1}=0 \ \)となるので,ラウスの安定判別法に沿ってラウス表を作成すると,ワンポイント解説「3.ラウスの安定判別法」の通り,
\[
\begin{array}{c|ccc}
& 1列 & 2列 \\
\hline
1行 & 1 & K_{2}+5 \\
2行 & 6 & K_{1} \\
3行 & \frac {6\left( K_{2}+5\right)-K_{1}}{6} & \\
4行 & K_{1} & \\
\end{array}
\]
となるので,
\[
\begin{eqnarray}
K_{1}>0 & ・・・・・・・・・ ①& \\[ 5pt ]
K_{2}+5>0 ⇔ K_{2}>-5 & ・・・・・・・・・ ②& \\[ 5pt ]
\frac {6\left( K_{2}+5\right)-K_{1}}{6} > 0 \\[ 5pt ]
6\left( K_{2}+5\right)- K_{1} > 0 \\[ 5pt ]
K_{1} < 6\left( K_{2}+5\right) & ・・・・・・・・・ ③& \\[ 5pt ]
\end{eqnarray}
\]
が成立するとき安定となる。したがって,まとめると,
\[
\begin{eqnarray}
0< K_{1} < 6\left( K_{2}+5\right) \\[ 5pt ]
K_{2}>-5 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。安定限界においては,\( \ K_{1} = 6\left( K_{2}+5\right) \ \)が成立するので,特性方程式は,
\[
\begin{eqnarray}
s^{3}+6s^{2}+ \left( K_{2}+5\right) s+6\left( K_{2}+5\right) &=&0 \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,\( \ s=\mathrm {j}\omega _{c} \ \)とおき,持続振動の角周波数を求めると,
\[
\begin{eqnarray}
-\mathrm {j}\omega _{c}^{3}-6\omega _{c}^{2}+ \mathrm {j}\left( K_{2}+5\right) \omega _{c}+6\left( K_{2}+5\right) &=&0 \\[ 5pt ]
6\left( K_{2}+5\right) -6\omega _{c}^{2}+ \mathrm {j}\left( K_{2}+5\right) \omega _{c}-\mathrm {j}\omega _{c}^{3}&=&0 \\[ 5pt ]
6\left\{ \left( K_{2}+5\right) -\omega _{c}^{2}\right\} + \mathrm {j}\omega _{c}\left\{ \left( K_{2}+5\right) -\omega _{c}^{2}\right\} &=&0 \\[ 5pt ]
\end{eqnarray}
\]
となり,実部虚部とも零でなければならないので,
\[
\begin{eqnarray}
\left( K_{2}+5\right) -\omega _{c}^{2} &=&0 \\[ 5pt ]
\omega _{c}^{2} &=&K_{2}+5 \\[ 5pt ]
\omega _{c} &=&\sqrt {K_{2}+5} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)目標値\( \ r \left( t\right) \ \)がランプ関数\( \ r \left( t\right) =t \ \)のときの定常速度偏差
\( \ R \left( s\right) \ \)から\( \ E \left( s\right) \ \)までの関係式は,
\[
\begin{eqnarray}
-E \left( s\right) \cdot K_{1} W \left( s\right) +R\left( s\right) &=&E \left( s\right) \\[ 5pt ]
\end{eqnarray}
\]
であるので,これを\( \ E \left( s\right) \ \)について整理すると,
\[
\begin{eqnarray}
R\left( s\right) &=&E \left( s\right) +K_{1} W \left( s\right) E \left( s\right) \\[ 5pt ]
&=&\left\{ 1+ K_{1}W \left( s\right) \right\} E \left( s\right) \\[ 5pt ]
&=&\left\{ 1+\frac {K_{1}}{s\left( s^{2}+6s+ K_{2}+5\right) } \right\} E \left( s\right) \\[ 5pt ]
&=&\frac {s\left( s^{2}+6s+ K_{2}+5\right) +K_{1}}{s\left( s^{2}+6s+ K_{2}+5\right) }E \left( s\right) \\[ 5pt ]
E \left( s\right)&=&\frac {s\left( s^{2}+6s+ K_{2}+5\right) }{s\left( s^{2}+6s+ K_{2}+5\right) +K_{1}}R\left( s\right) \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,ワンポイント解説「1.基本的なラプラス変換」の通り,ランプ関数\( \ r \left( t\right) =t \ \)のラプラス変換\( \ \displaystyle R \left( s\right) =\frac {1}{s^{2}} \ \)なので,これを代入し,定常速度偏差を求めると,ワンポイント解説「4.最終値の定理」の通り,
\[
\begin{eqnarray}
\displaystyle \lim _{ t \to \infty } e(t)&=&\displaystyle \lim _{ s \to 0 } sE(s) \\[ 5pt ]
&=&\displaystyle \lim _{ s \to 0 } \left\{ s\cdot \frac {s\left( s^{2}+6s+ K_{2}+5\right) }{s\left( s^{2}+6s+ K_{2}+5\right) +K_{1}}\cdot \frac {1}{s^{2}} \right\} \\[ 5pt ]
&=&\displaystyle \lim _{ s \to 0 } \left\{ \frac {s^{2}+6s+ K_{2}+5}{s\left( s^{2}+6s+ K_{2}+5\right) +K_{1}} \right\} \\[ 5pt ]
&=&\frac {K_{2}+5}{K_{1}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)a.\( \ K_{1} \ \)を固定したとき,\( \ K_{2} \ \)を大きくすると,速応性と定常特性はどのように変化するか
(1)及び(2)解答式より,\( \ K_{2} \ \)を大きくすると,\( \ U \left( s\right) \ \)から\( \ Y \left( s\right) \ \)までの伝達関数が小さくなり,ゲインが低下する。ゲインが低下するとフィードバック制御系の速応性は低下する。また,(4)解答式より,\( \ K_{2} \ \)を大きくすると,定常速度偏差が増大するため,定常特性としては劣化する。
(5)b.\( \ K_{2} \ \)を固定したとき,\( \ K_{1} \ \)を大きくすると,減衰特性と定常特性はどのように変化するか
(3)の安定条件より,\( \ K_{1} \ \)を大きくすると安定限界に近づくため振動的になり減衰特性は悪くなる。また,(4)解答式より,\( \ K_{1} \ \)を大きくすると,定常速度偏差が低下するため,定常特性としては改善する。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは